Physics-Informedニューラルネットワーク wi2 ニューラル演算子
日本では、2020年6月30日に宇宙基本計画ver.1が閣議決定された(ver.2は、2023年6月13日閣議決定)。20年5月には、日本の宇宙利用の優位を確保するため、航空自衛隊府中基地に「宇宙作戦隊」が新編された。宇宙領域把握(SDA)に関する取組(防衛省、2023年11月28日)†1では、「宇宙作戦能力を強化するため、SDA体制の整備を確実に推進することが重要である」と強調されている。経団連も、「宇宙の安定的な利用を確保するためには、デブリや不審な衛星の動向など宇宙の状況を把握する必要がある」として、「SDA衛星の2026年度打上を達成すべきである」と主張している†2(もっとも、防衛省の意向を汲んでいるだけだろう)。
米MITリンカーン研究所†3は、「人工衛星に作用する”モデル化されていない加速度”をPINNsで学習することで、衛星軌道を正確に予測できた」と主張する論文(以下、本論文[*85])を公開した(24年3月28日@arXiv)。 ☛モデル化されていない加速度は、後述。
†1 https://www8.cao.go.jp/space/comittee/27-anpo/anpo-dai58/siryou2.pdf
同資料において、以下のように用語定義が行われている。SDAは、SSAに加えて「宇宙機の運用・利用状況及びその意図や能力を把握すること」。SSAは宇宙状況把握(Space Situational Awareness)の略語であり、「宇宙物体の位置や軌道等を把握すること(宇宙環境の把握を含む)」。
†2 https://www.keidanren.or.jp/policy/2024/017_honbun.html
†3 米連邦政府機関御用達大学であるMITにおける、航空防衛(攻撃に使用される研究はしないらしい)に特化した研究所。国防総省が設立した研究所の運営をMITが受託しているという、米国でよくある形態。古い資料(https://repository.dl.itc.u-tokyo.ac.jp/record/21065/files/sk029007015.pdf)によれば、年間予算の約90%が国防総省との契約に基づく収入である。
【1】本論文の主張
「逆問題、外挿」というPINNsにとって得意なワードが含まれている。
(1) PINNsによって、「対地同期軌道†4(GEO)上の人工衛星に作用する、”モデル化されていない加速度”を、学習することができた」。これは、衛星軌道調整(フィッティング)の文脈で、逆問題を解いたことを意味する。 ☛モデル化されていない加速度は、後述。
(2) PINNsは、20日後の衛星軌道を高精度に予測できた。これは、外挿が、高精度に行えたことを意味する。
†4 赤道上の対地同期軌道は、静止軌道と呼ばれる。
【2】事前整理
(1) モデル化されていない加速度
軌道状態†5を、物体と相関する観測値に適合させることによって、衛星軌道は維持される。観測値は、宇宙監視専用の光学センサーとレーダー センサーで構成される宇宙監視ネットワークによって得られる。米国では、衛星軌道の維持は、米国防総省の一部である、第18宇宙防衛飛行隊によって行われている(らしい)。
過去数十年にわたり、衛星が軌道を変更するためにスラスターを積極的に使用していないことを前提として、衛星が「いつ・どこに存在しているか?」を、迅速かつ正確に予測するために使用できる、高忠実度の物理モデルが開発されてきた。それらの高忠実度物理モデルは、地球重力、大気抗力(大気ドラッグ)、太陽輻射圧(SRP)効果、太陽・月・その他の天体からの重力摂動なども考慮する、高品質な物理モデルである。たとえば、2行軌道要素形式(Two Line Element set:TLE)†6から衛星の位置と速度を予測するために使用される Special General Perturbations 4(SGP4)プロパゲータは、地球の重力、大気抵抗、太陽と月による摂動を考慮している。しかし、衛星の推力は考慮されていない。この衛星推力は、モデル化されていない加速度の発生源の一つである。
常駐宇宙物体(Resident Space Object:RSO)†7の中には、モデル化されていない加速度を考慮しなければ、軌道予測が困難なRSOが存在する。例えば、㊀軌道を変更するために、低推力の電気推進(☛下記(1)を参照)を使用する衛星や、㊁既存のモデルで考慮されている以上の SRP 効果を受ける非常に高い面積質量比(HAMR)を持つデブリ、があげられる。
†5 2行軌道要素形式(TLE)または、位置および速度ベクトルのいずれか。TLEは、下記†6を参照。
†6 TLEとは、北米航空宇宙防衛司令部が、監視し公開している人工衛星を含む宇宙物体の軌道情報
を2行形式で表したもの
(出所https://gportal.jaxa.jp/gpr/assets/mng_upload/GCOM-W/TLE.pdf)。
†7 RSOには、活動中・非活動中の宇宙船、ロケット本体や(ロケットの)上段、制御不能なスペースデブリなどが含まれる
(出所https://crds.jst.go.jp/dw/20240402/2024040237805/)。
(2) 軌道予測が困難な理由
前項で、 モデル化されていない加速度を考慮しなければ、軌道予測が困難なRSOも存在することを述べた。その理由を整理しよう。以下では、分かり易さを優先して、RSOを人工衛星に限定する。今日、衛星の大部分は、何らかの推力を使用して正確な軌道を維持している。特に、電気推進(イオン推進、ホール効果スラスター、パルスプラズマスラスターなど)は燃料効率が向上するため、よく利用されている。
電気推進システムと化学スラスタの重要な違いの 1 つは、化学スラスタは数秒で大きな加速を達成できるのに対し、電気推進システムは数分から数日間継続的に低推力を適用すること、である。化学スラスターを使用して短期間に大きな加速を加える衛星の場合、軌道状態の変化が瞬間的に起こる。このため、センサーにタスクを割り当て、衛星の新しい観測値を関連付け、操縦後の新しい状態を推定する機会が与えられる。端的に述べると、未知のノイズが混入するするものの、短期間であるため、衛星のダイナミクスによる影響は軽微(従前のダイナミクスは、失われていない)と表現できるだろう。
一方、低推力を数日間継続的に適用する電気推進システムを使用する衛星(以下、「推進衛星」と呼称)は、軌道移動操作終了時の衛星位置は、操作開始時の位置から、非常に遠く離れている可能性がある。そのため、新しい観測値を、衛星の以前の軌道状態と明確に関連付けることは困難である。これも端的に述べると、長期間に渡って未知のノイズが混入したため、従前のダイナミクスに関する知識はもはや失われた、と表現できるだろう。従って、新たにダイナミクスを構築する必要がある(しかも、電気推進システムを使用する度に、継続的に)。
推進衛星の軌道状態は、実態として、試行錯誤的な手動介入によって維持されている。この手動介入は、絶えず変化する軌道状態に対応するために、頻繁に繰り返す必要がある(ので時間とコストを要する)。また、手動介入による維持では、例えば光学センサー・サイトの気象停止等により、新しい観測値がすぐに受信されない場合、推進衛星が完全に失われる可能性がある。
【3】本論文のアイデア
(1) モデルの学習
1⃣ モデルの構築指針
推進衛星における軌道変更後のダイナミクスを構築するには、衛星に作用する自然力と人工推力の両方を含む、衛星の総加速度を計算するモデルを構築する必要がある。本論文は、このモデルを「物理モデルと深層学習モデルの組み合わせ」により構築する。具体的には、Physics-Informedニューラルネットワーク(PINNs)を適用する。当該軌道予測の問題形式が逆問題であり、さらに外挿の成功が有用であるため、PINNsが選択されたと考えられる。
簡単にまとめると、PINNsにおいてモデル化する物理量は、推進衛星に働く「加速度」である。モデル出力は、推進衛星の(衛星軌道上の)位置及び速度である(速度については、分かり易さを優先して、本稿では触れていない)。位置=∫(∫加速度dt)dtなので、モデル・アーキテクチャ的には、ニューラルODEと見做すことができる。
2⃣ 損失関数
当該PINNsに使用される損失関数は、観測残差の平均二乗誤差(MSE)である。衛星の位置ベクトルと速度ベクトルは、軌道伝播†8によって決定される。(軌道伝播によって決定された)位置ベクトルと速度ベクトル⊕センサーの位置と速度、から予測観測値を導出できる。次に、これらの予測観測値が、実際の観測値と比較され、合計損失関数が計算される。合計損失関数とは、物理モデルからの損失関数+人工推力に対応する深層学習モデルからの損失関数、である。後者は、「逆問題の損失関数」という解釈もできる。この合計損失関数は、モデル パラメーターに関する勾配を決定するために、ODEソルバー†9を通じて逆伝播される。
3⃣ 初期条件の調整
モデル学習プロセスの一部として、ネットワーク・パラメーターに加えて、衛星の初期位置と速度ベクトルも調整される。これは、㈠モデル内に調整可能なパラメーターとして初期条件を含めるか、㈡これらのパラメーターをモデルから除外して個別に解決する、ことによって実現できる。本論文では、両者が評価され、㈡がより優れていると判明した。
具体的には、初期条件は、学習ループの N 回の反復ごとに 1 回、観測データに適合する単純なバッチ最小二乗法を使用して推定される。100学習ステップごとに、初期条件をフィッティングすると、良好なパフォーマンスが得られることがわかった。
†8 ある時刻にある位置・速度で運動をしている人工衛星が、その後の時刻において、どの位置・速度にいるのかを計算すること。
†9 (常)微分方程式ソルバー
(2) ニューラルネットワークのハイパーパラメータ等
アーキテクチャ・・・多層パーセプトロン
隠れ層数・・・2
活性化関数・・・tanh(双曲線正接関数)
オプティマイザ・・・Adam
エポック数・・・2万
学習率初期値・・・3×10-3
学習率スケジューリングのステップサイズ・・・100
学習率スケジューリングのスケールファクター・・・0.98
(3) データセット
地上のパッシブ光学望遠鏡から観測された、GEO上にある推進衛星の角度のみを、入力データとする。データは 2 日間にわたり、赤経と赤緯†10において30 回測定され、時間内にランダムにサンプリングされた。 測定誤差は、平均値ゼロ、標準偏差0.5秒角のガウス分布を、ランダム・サンプリングすることにより観測値に追加された。
†10 赤経(right-ascension:RA)は、春分時の太陽の位置を0時とし、地球の自転の方向に24時まで定めた方位。赤緯(declination:Dec)は、天の赤道を 0°とし、北極方向を正として±90°まで定めた角度。
【4】比較結果
(1) 比較対象と比較指標
❶PINNsと比較されるモデルは、❷物理モデル単体である。本論文のPINNsは、物理モデルと深層学習モデルを組み合わせモデルであった。比較指標は、二乗平均平方根誤差(RMSE)である。
(2) 観測誤差と外挿誤差
1⃣ 観測誤差
PINNのRMSEは 1.00秒角。一方、物理モデル単体のRSMEは、123 秒角であり、2 桁改善された。
2⃣ 外挿誤差
モデルが、衛星軌道をどの程度正確に予測できるかを評価した。学習期間終了から1日後、5日後、20 日間後の、予測伝播位置と真の伝播位置との差(km)を算出し、比較した(20 日間後は図からの目分量)。結果は、1日後❶3.35km❷397km、5日後❶164km❷3,860km、20日後❶およそ1万5,000km❷およそ3万5,000km、である。1日後は2桁の改善、5日後は1桁の改善、20日後は2倍程度の改善である。静止軌道を3万6千kmとすると、静止軌道の周長は226万km程度だから、周長の1/10程度ズレている計算になる。
【5】感想
(1) PINNsに限らず、どのようなツール・アルゴリズム・アーキテクチャ・方法論でも、唯一無二の絶対王者は存在しない。必ず、得手不得手がある。機械学習・深層学習に限定すれば、唯一無二は存在しないことが証明されている(らしい)。PINNsも、非線形性問題に弱いと指摘され、意外と有効範囲が狭いという評価を受けているように思える。しかし実務家として重要なことは、手持ちのツールが有効な領域を特定し、そこで違いを出すということであろう。その意味で、本論文は、面白いところにPINNsを適用したと感じる。
(2) 本論文の学習データ(入力データ)は、角度のみである。地上のパッシブ光学望遠鏡で正確に観測できる値だけを使用している。レーダーセンサーを使うと、距離と測度の情報も取得できる。普通に考えて、入力データをリッチにすると、出力(結果)もリッチになると思われる。そこは、敢えて公開していないのだろうか。
ニューラルネットワーク(NN)を使った代理モデルは、その洗練さ、柔軟性の高さ、観測データの組み込みの容易さにより、従来の数値ソルバーに代わる魅力的な選択肢と期待されている。PINNsはNNを使った代理モデルの代表と考えられているものの、誤った解に収束することも多く、その学習は難しいことが知られている。このPINNsにおける学習の困難を、本稿ではシンプルに、学習障害と呼称する。
ニューラルネットワークによる学習モデル(深層学習モデル)の性能は、極端に言えば、全てデータにかかっている。この教義をPINNsにあてはめると、PINNsの性能は、損失(関数)に関する最適化計算に用いるデータが全て、ということになる。ここで、学習障害対策の先行研究を概観すると、[*40]では、以下の3つを上げている:㊀時間的因果関係の尊重(【2】(2)2⃣参照)、㊁PINNsの損失関数(PDE†0損失、初期損失、境界損失)にかかる重みを、適応的に調整する、㊂カリキュラム学習。また、[*74]では、PINNsの課題に対する対策(の一つ)として、損失関数にかかる重みの変更及び、再サンプリングを上げている。
教義にあてはめるとデータが全て、である。コロケーション点が十分にあればPINNsの性能は高くなるが、同時に計算コストも高くなる。PINNsを代理モデルとして用いる場合、数値ソルバーより計算が遅ければ意味がない(場合により、PINNsが有限要素法より遅い、という論文はこちら)。そこで、コロケーション点の数に関して、良い塩梅を探す意味が出てくる。
PINNsに文脈におけるコロケーション点とは、数値が紐付いた点を意味する。ここで言う数値とは、入力値並びに出力値である。先行研究を見ると、間接的にコロケーション点を調整していることがわかる(※)。損失にかかる重みを調整して、間接的×間接的にコロケーション点を調整するか、サンプリングで間接的にコロケーション点を調整している。本稿では、コロケーション点の構成を扱った論文を2つ取り上げている。一つ目の[*87]は、コロケーション点を直接調整するアプローチを扱っている。二つ目[*88]は、サンプリングで間接的にコロケーション点を調整するアプローチを扱っている。
†0 物理や数理解析の文脈でPDEは、偏微分方程式(Partial Differential Equation)の略であるが、本稿では意図的に混同して、支配方程式そのものに対する略称にもPDEをあてる。
※ 「間接的にコロケーション点を調整している、という統一的な見方が可能」という表現が、正しいかもしれない。間接的の意味が分かり難いが、間接≠直接であり、「書き下せる規則に従って、コロケーション点を(直接)拾い上げる」ことを直接(的)と言っている(つもり)。
【1】論文の主張
(0) 前説
フィンランド・アールト大学[*86]の研究者は、「アルゴリズムを改良して、PINNs学習の安定性を高めた」を主張する論文[*87]を発表した(23年1月11日@arXiv)。学習の安定性については、【7】(1)を参照。結構重要な論文だと思っている。
英リーズ大学及びロンドン大学の研究者による論文[*88](24年4月18日@arXiv)は、幅広いケースで優れた性能を示すサンプリング手法を構築した、とする。
(1) [*87]の主張
「相対L2誤差†1を小さくできる、バニラPINNsに対するアルゴリズムを開発した」と主張する。この場合のアルゴリズムは、損失(関数)に対する最適化計算用コロケーション点を構成するアルゴリズムである。開発したアルゴリズムの有効性を、対流方程式に加えて、反応方程式・反応拡散方程式・拡散方程式に対して、実証した。
†1 為念:相対L2誤差=||真値ー予測値||2/||真値||2。||・||2は、L2ノルム(≒ユークリッド距離)。
(2) [*88]の主張
PDE損失の計算に用いるコロケーション点のサンプリングにおいて、「独立変数に関する残差の混合微分に基づく、コロケーション点位置の確率分布を使った、適応サンプリングは優れている」と主張する。対象とした方程式はバーガース方程式とアレン=カーン方程式であり、多種多様なケースで、固定サンプリング等と比較した。
【2】事前整理
(1) 学習障害の原因と対策
[*87]では、学習障害の原因を、以下のように特定している。まず、PINNsの実際の失敗例から、次の洞察を得た:PINNs が一部の領域(たとえば、初期条件から遠く離れた領域)で、単純†2で局所的に一貫した解を見つけると、それを変更するのは非常に困難になる場合がある。これにより、正しい解と間違った解を組み合わせた、最終的な解が得られてしまう。
その上で、学習障害を次のように整理した:「初期条件から遠く離れた点」が、PINNsのPDE損失に寄与する場合、解を悪い局所最適に向かって引っ張ることによって最適化手順を悪化させる可能性がある。一方、学習開始時点において、PDE損失に「初期条件から遠く離れた点」を含めることには、ほとんど利点がない。
そのように学習障害を理解した上で、対策を考案した:損失関数の最適化計算に用いるコロケーション点を、規準に則って構成する(☛【3】(2)参照)。
†2 空間的な構造を示さない、均一・一様な解を単純と呼んでいるようである。
(2) [*87]における学習障害対策の先行研究整理
1⃣ 時間適応戦略
時間区間を部分区間に分割し、各部分区間で PINNs を順次学習することにより、学習障害に対処するアプローチは、時間適応戦略と呼ばれる。 時間適応戦略により、PINNs の学習手順は、初期条件から時間区間のもう一方の端(終端点)に向かって、徐々に移動する解を計算する、古典的数値ソルバーと同様になる。 少しだけ詳しく述べると、時間区間[T1、T2]が複数の部分区間に分割され、PDEは個別の PINN によって、部分区間ごとに順番に解かれる。前の部分区間の境界にある解が、次の部分区間の初期条件として使用される。
2⃣ 時間的因果関係の尊重
”時間依存”PDE を解くときに PINNs が時間的因果関係に違反する可能性があるため、誤った解に収束しやすいことが示されている。これは、PINNs がすべての PDE残差を同時に最小化する傾向がある一方で、初期の正しい解を取得する前であっても、後の時点で PDE残差を最小化する方向に望ましくない偏りがあるためである。
この問題の対応策は、時間軸に沿った重み「時間的重み」を導入することである。この重みは(時間軸上で)直前のPDE累積損失を使用して計算される。当該対応策の本質は、(時間軸上で)以前のすべての点で、解が適切に近似されるまで、初期条件から遠く離れた点の影響をゼロにすることである。
(3) [*88]によるコロケーション点サンプリング手法の整理
1⃣ 概要
PINNsのオリジナル実装では、固定数のコロケーション点が系全体に、ランダムかつ均一に分散される。ただし、特定の問題では、一部の領域は他の領域よりも本質的に学習が難しく、純粋にランダムなアプローチでは学習が遅くなったり、非効率になったりする可能性がある。異なるコロケーション点には、異なる量の学習情報が含まれる。これは、コロケーション点の分布を調整することが、学習効率の点で有益である可能性を示唆する。また、コロケーション点の分布調整は、学習中にネットワークが極小値に陥るリスクを最小限に抑えることにも繋がる(ので有益である)。
ただし、どの領域が最も重要になるかについての先験的な知識が必要である等の理由により、コロケーション点の分布を、手動で調整するのは困難である。単純な代替案は、コロケーション点の数を増やすことであるが、計算コストが大幅に増加する。実用的な意味での、コロケーション点の最適な分布または良好な分布を見つける手法としては、 2 つの一般的なアプローチがある。
㈠ 固定されたコロケーション点を持つが、それらの重み付けを異なる方法で行う。つまり、適応重み付け、である。領域内における、特定コロケーション点の影響を重み付けして、主要なコロケーション点が見落とされないようにする。
㈡ コロケーション点の位置を調整する。つまり適応(型)再サンプリングである。
2⃣ サンプリングの規準
サンプリングの観点から見ると、既存方法は基本的に、明示的なパラメータ化、または陰的近似のいずれかを介して、コロケーション点の理想的な分布を求める。理想的な分布を求めるために利用されている情報は、コロケーション点における局所PDE残差や、コロケーション点の位置に関する損失関数の導関数など、主に損失関数に焦点を当てている。
これに対して[*88]は、推定解と残差の混合導関数に基づいた代替規準を検討する。
【3】[*87]が開発したアルゴリズム
(1) アルゴリズムの概要とセットアップ
0⃣ 概要
[*87]のPDEは、初期値・境界値問題として解かれる、という設定である(もちろん、これは標準的な設定)。その設定の下、[*87]で提案されている、学習障害を解消するPINNs学習アルゴリズムは、時間軸と空間軸の双方で工夫がなされている。
時間軸では、時間適応戦略を踏襲する。時間適応戦略は、時間区間を分割して、分割した部分区間ごとにPINNs学習を行う。このため結果的に、異なる初期値で学習を行う形式の「アンサンブル学習」となる。空間軸では、損失に関する最適化計算用コロケーション点(以下、単に、コロケーション点)を拾い上げていくする領域を規準に則って、徐々に拡大するというアプローチを採用する。
1⃣ アンサンブル一致度
PINNアンサンブルのメンバーは通常、コロケーション点近傍では同じ解に収束するが、コロケーション点から遠く離れたところでは、異なる間違った解を好む可能性がある。このため、アンサンブルの一致度を、「コロケーション点をPDE損失を計算する点に含める」ための規準として使用することができる。なお、上記「コロケーション点をPDE損失を計算する点に含める」の意味は、アンサンブル一致度によって追加(条件を与える点が追加及び、新しい初期条件が追加)された初期条件を使って、PDE損失計算を行うという意味である。アンサンブル一致度は、アンサンブル学習で出力される予測値(以下、アンサンブル予測値)の分散として計算される†3。
2⃣ セットアップ
初期損失を計算する初期条件データセットをDとする。境界損失計算用コロケーション点候補の集合をB、実際に選択されたコロケーション点の集合をB’とする。同様に、PDE損失に対して、PとP’を設定する。
†3 [*87]で、言葉で明示されているわけではないが、アルゴリズム(5頁のAlgorithm 1 Training PINNs with label propagation)において表現されている。
(2) アルゴリズムの詳細
1⃣ 詳細アルゴリズム壱・PDE損失
アルゴリズムは、以下の通りである:Dの中で、PDE損失に関するソフト制約†4を満たす点の集合を、まず作成する。この集合をD’とする。ソフト制約は、アンサンブル予測値の平均に対して課されている。D’の点とPの点との最短距離が、”しきい値”†5未満の点を抽出して、P’を作成する。つまり、PDE損失は、初期条件を設定した点との距離が近い点から計算が実行される。この「楽な箇所から初めて、困難な箇所に進む」というアプローチは、カリキュラム学習と発想が似ている。
DはPの点を一部加えて、ゆっくり膨張していく(下記3⃣を参照)。膨張したDをD+と表現する。このためP’を構成する点は、Dから見て遠く離れた点を、徐々に加えていく(=PDE損失を計算するコロケーション点が拡大していく)仕組みになっている。なお、コロケーション点の構成は、コロケーション点候補の全てに、当該アルゴリズムが適用されるまで継続される(これは、境界損失、初期損失でも同様)。
2⃣ 詳細アルゴリズム弐・境界損失
PDE損失の場合とアルゴリズムは、同じである:D’の点とBの点との最小距離が、”しきい値”†5(再)未満の点を抽出して、B’を作成する。境界損失も、初期条件を設定した点との距離が近い点から計算が実行される。
3⃣ 詳細アルゴリズム参・初期損失
初期損失の場合のアルゴリズムは、他と大きく異なる:P’の(コロケーション)点を使って求めたアンサンブル予測値に対して、中央値と分散を計算する。次の㈠及び㈡が満たされれば、P’のコロケーション点における、アンサンブル予測値の中央値を「疑似的な初期値†6」とする:㈠分散がしきい値未満†7。㈡P’のコロケーション点とD’の点との最短距離が、しきい値未満†8。P’のコロケーション点と「疑似的な初期値」がDに追加され、D+となる。
†4 ε未満で十分であることを意味する。[*87]では、ε=0.001(デフォルト値)。
†5 具体的には、0.1(デフォルト値)。
†6 [*87]では、「擬似ラベル」と呼ばれている。
†7 この場合のしきい値は、4×10-4(デフォルト値)。
†8 この場合のしきい値は、0.05(デフォルト値)。
(3) 2つのバージョンと損失関数の重み
[*87]では、損失関数の重みを適応的に変化させるというアプローチを採用せず、固定数として扱う。損失関数の重みが固定数の場合、重み=損失関数を計算するために用いるコロケーション点の数、とすることは、普通である。
❶アンサンブル・バージョンの場合、損失関数の重みは、次のように設定される:境界損失の重みwB = 1/|B’|、PDE損失の重みwPDE= 1/|P’| 及び初期損失の重みwS= 1/|D|。ここで、アンサンブル・バージョンとは、PDE損失の計算にのみ、D+を使用するバージョンを指している†9。|B’|は、境界損失を計算するために用いるコロケーション点の数である。|P’|は、PDE損失を計算するために用いるコロケーション点の数である。|D|は、初期失を計算するために用いるコロケーション点の数であり、初期条件を与える点+擬似ラベル点の数である†10。
❷擬似ラベル・バージョンの場合、損失関数の重みは、次のように設定される:境界損失の重みwB = 1/|B’|、PDE損失の重みwPDE= 1/|P’| 及び初期損失の重みwS= 1/|D+|。擬似ラベル・バージョンとは、D+を使用して、PDE損失と初期損失の両方を計算するバージョンを指している。
以降、❶及び❷を『提案手法』と呼称する。
†9 [*87]内でアルゴリズムを説明している箇所(5頁のAlgorithm 1 Training PINNs with label propagation)では、アンサンブル・バージョンは、D+を使わずにDを使うと書かれている(ただし、[*87]の表記は、DがDLで、D+はDL∪DPL)。これは、6頁の記述(2. PINN Ensemble (Ens):)と整合がとれていない。本稿では、6頁の記述を正としている。
†10 擬似ラベル点の数を加えていることは、矛盾するのではないかと思うが、原論文ママ。
(4) まとめ
アンサンブル学習である[*87]のPINNsに対する、工夫された学習アルゴリズムは、規律のとれたコロケーション点の構成とまとめることができるだろう。無計画で野放図に構成するのではなく、初期条件を与える点の近くからPDE損失用のコロケーション点を、徐々に拾い上げていく。こうすることで、悪い影響しかもたらさないコロケーション点を除外している。
(5) ハイパーパラメータ等
Adamの学習率・・・1.0×10-3
隠れ層の数・・・4
隠れ層のニューロン数・・・50
活性化関数・・・tanh(双曲線正接関数)
LBFGS†11適用のタイミング・・・PDE損失に寄与するコロケーション点の更新前と学習の最後。
†11 LBFGSはL-BFGSとも表記される。
【4】[*87]の検証結果
(0) 検証の対象とした物理系(支配方程式)
掲題の物理系は、以下の通りである。なお、コロケーション点の数は、PDE損失が1,000、初期損失が256、境界損失が100である。
① 周期的境界条件を課した、対流方程式
② 周期的境界条件を課した、化学反応のモデル化に使用される反応システム
③ 周期的境界条件を課した、反応拡散方程式
④ 周期的境界条件を課した、拡散方程式
⑤ ディリクレ境界条件を課した、拡散方程式
(1) 提案手法との比較:比較対象モデル及び、比較指標
比較対象としたPINNsは、以下の4種類である:⓵バニラPINN、⓶SA-PINN、⓷時間的因果関係を尊重したバニラPINN(☛【2】(2)2⃣参照)、⓸bc-PINN。以降、⓵~⓸を『既存手法』と呼称する。なお、表記は[*87]に従った。
SA-PINNは、Self Adaptive-PINNの略であり、損失関数の重みを自己適応的に変化させる。本質的には、解の導出(つまりは、パラメータ導出に関する最適化計算に相当する)に重要な領域から、多くサンプリングすることで、学習性能をあげる。
bc-PINNは、backward compatible PINNの略である。bc-PINNの問題意識は、非線形性が強く高次の偏微分方程式に対しては、PINNの精度は著しく低下する、ということである。そして、この問題を解決するために、単一のニューラルネットワークを用いて、連続する時間区間にわたってPDEを逐次的に解くというスキームを提示した。[*87]でいうところの、時間適応戦略を採用した、アンサンブル学習である。bc-PINNは、サンプリングに工夫を凝らしておらず、時間区間の分割及びサンプリングが固定的である。
[*87]では具体的には、時間区間は4分割され、PDE損失を計算するために各区間で 250 個のコロケーション点を構成し、境界損失を計算するためには25 個のコロケーション点を構成している。
比較指標である相対L2誤差は、異なるランダム・シードを使用した10回の学習過程にわたる平均値として算出した。
(2) 記述手法と提案手法との比較結果
0⃣ 比較に関する詳細
既存手法は既述済だが、オプティマイザを含めて、詳細に記述する。
基本的に、 オプティマイザは、㊀Adam、㊁LBFGS、㊂Adam+LBFGS、が使用された。ただし、⓷はAdamのみ(と思われる)。また、⓶のオプティマイザは、①~③においてはAdamのみであるが、④と⑤では、Adam及びAdam+LBFGSが使用されている。提案手法では、㊀と㊂が用いられ、㊁は用いられていない。
既存手法は、①~③では、物理パラメータを2パターン考慮するので、それぞれ14種類存在する: (⓵3種+ ⓶1種+⓷1種+⓸2種)×2パターン=14種類、である。④と⑤では、物理パラメータを3パターン考慮するので、21種類存在する:(⓵3種+ ⓶2種+⓸2種)×3パターン=21種類、である。提案手法は、①~③では(❶2種類+❷2種類)×2パターン=8種類、④と⑤では(3パターンなので)12種類である。
1⃣ 実際の比較結果
大きな傾向を示すため、①~⑤について、相対L2誤差が10-3である割合、10-2である割合・・・等を示す。最高性能を示した組み合わせも、併せて示す。
① 既存手法:10-4|0.00%、10-3|7.14%、 10-2|28.57%、10-1|50.00%、100|14.29%
提案手法:10-4|0.00%、10-3|50.00%、10-2|50.00%、10-1|0.00%、 100|0.00%
最高性能は、❷with㊂である。
② 既存手法:10-4|0.00%、10-3|35.71%、10-2|28.57%、10-1|35.71%、100|0.00%
提案手法:10-4|0.00%、10-3|62.50%、10-2|37.50%、10-1|0.00%、 100|0.00%
最高性能は、実は、⓸with㊂である。
③ 既存手法:10-4|0.00%、10-3|42.86%、 10-2|0.00%、10-1|57.14%、100|0.00%
提案手法:10-4|0.00%、10-3|100.00%、10-2|0.00%、10-1|0.00%、 100|0.00%
最高性能は、⓶である。
④ 既存手法:10-4|14.29%、10-3|38.10%、10-2|23.81%、10-1|23.81%、100|0.00%
提案手法:10-4|33.33%、10-3|33.33%、10-2|33.33%、10-1|0.00%、 100|0.00%
最高性能は、❶with㊂ である。
⑤ 既存手法:10-4|14.29%、10-3|38.10%、10-2|33.33%、10-1|14.29%、100|0.00%
提案手法:10-4|33.33%、10-3|33.33%、10-2|33.33%、10-1|0.00%、 100|0.00%
最高性能は、❶with㊂ である。
2⃣ 小括
最高性能だけを取り上げると、既存手法でも遜色がないように見えるかもしれない。しかし、”安定性”で捉えると、相対L2誤差が、10-2で収まっている提案手法に軍配が上がる。とは言え、物理系を変えて、さらに物理パラメータを変えると、違った景色が見えてくるはずなので、提案手法が飛び抜けて優秀ということではない(だろう)。
(3) ❶と❷の比較
一概には言えない(ところが悩ましい)。①及び②では、❷with㊀の性能が著しく低い。③~⑤では、その傾向は見られない。また、①~③では❷with㊂の性能が最も高い。④~⑤では、ほぼ❶with㊂の性能が最も高い。
オプティマイザで言えば、㊀よりも㊂の性能が、ほぼ高い。
【5】[*88]の構成
(0) 概要
[*88]で行いたいことは、以下である:(バーガース方程式、アレン=カーン方程式)×(物理パラメータ、初期条件、コロケーション点数、再サンプリングの回数)という、多種多様な組み合わせに対して、6つのサンプリング手法を適用する。どの組み合わせに対しても、「相対L2誤差が小さい」サンプリング手法があれば、それを発見する。
なお[*88]では、損失関数=データ損失+PDE損失+境界損失とした上で、「順問題なのでデータ損失は考慮しない」、「境界損失にはハード制約を課す」ので、最適化計算の対象はPDE損失のみである。ここでの境界損失は、初期損失を含む(含んでも良い)。
(1) サンプリング手法
6つのサンプリング手法を適用する:⓵一様ランダム分布に従うサンプリングを行う。⓶Hammersleyサンプリング†12を行う。⓷”現時点”の残差等を反映した確率分布関数に従うサンプリングを行う。ただし、初期分布はランダム分布。⓸基本的に⓷と同じ。違いは、初期分布のみで、初期分布からのサンプリングはHammersleyサンプリングに従う。⓹”現時点”の推定解の2次導関数(空間微分と時間微分の混合微分:∂2/∂t∂x)を反映した確率分布関数に従うサンプリングを行う。⓺”現時点”の残差の2次導関数に基づく(つまり、∂2/∂t∂x)を反映した確率分布関数に従うサンプリングを行う。
†12 ディスクレパンシー(discrepancy)が小さい擬似乱数”数列”である、Hammersley点群を使ったサンプリング。Hammersley点群は、有限個の点から成るため、数列と呼ばず点群と呼ぶ(らしい)。ディスクレパンシーが小さい数列の他例として、Halton数列、Sobol数列、GFSR(Generalized Feedback Shift Register)数列、Good Lattice点群などがある。ディスクレパンシーとは、乱数の均一さを表す尺度である。その値が小さいほど、乱数は均一である(つまり、真の乱数に近い)。Hammersley点群のディスクレパンシーは、Halton数列より小さい(らしい)。
(2) 検証に用いた物理系のセットアップ
①1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,30,40,50,75?,100}回実施。
②1次元バーガース方程式。コロケーション数{250,300?,500,750,1000,2000}。物理パラメータν=π/100。初期条件u(x,0)=-sin(πx)。再サンプリングを100回実施。
③1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、3つの低周波数正弦関数を、ランダムに重み付けした関数をu(x,0)とする。再サンプリングを{10,20,30,50,100}回実施。
④1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、4つの高周波数正弦関数を、ランダムに重み付けした関数をu(x,0)とする。再サンプリングを{10,20,30,50,100}回実施。
⑤1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、u(x,0)=sin(2πx)†13。再サンプリングを{10,20,30,50,100}回実施。
⑥1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、u(x,0)=1.5×sin(πx)†14。再サンプリングを{10,20,30,50,100}回実施。
⑦1次元バーガース方程式。コロケーション数2,000。物理パラメータν=0.01。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑧1次元バーガース方程式。コロケーション数2,000。物理パラメータν=0.001。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑨1次元バーガース方程式。コロケーション数1,000。物理パラメータν=0.01。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑩1次元バーガース方程式。コロケーション数4,000。物理パラメータν=0.001。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑪アレン=カーン方程式。コロケーション数500。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
⑫アレン=カーン方程式。コロケーション数1,000。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
⑬アレン=カーン方程式。コロケーション数2,000。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
†13 [*88]では、u(x,0)=sin(2π)となっているが、それでは恒等的に0なので、sin(2πx)とした。
†14 [*88]では、u(x,0)=1.5×sin(π)となっているが、それでは恒等的に0なので、1.5×sin(πx)とした。
(3) ハイパーパラメータ等
Adamの学習率・・・1.0×10-3
隠れ層の数・・・3
隠れ層のニューロン数・・・64
活性化関数・・・tanh(双曲線正接関数)
LBFGS適用のタイミング・・・Adamの初期 15,000 ステップに続いて LBFGS の 1,000 ステップ。その後 2,000ステップごとに再サンプリング。再サンプリングは、最初の1,000ステップがAdamで、続く1,000ステップが LBFGS。
【6】[*88]の検証結果
(1) 比較指標
比較指標である相対L2誤差は、異なるランダム・シードを用いた20回の学習過程にわたる平均値として算出されている。
(2) 比較検証の結果
①→ 相対L2誤差の水準は、良くて、10-4~10-3。⓵⓶が全くダメで、⓷は不安定、⓹がやや悪く、⓸と⓺が良い結果。
②→ 相対L2誤差の水準は、良くて、10-4~10-3。⓶はコロケーション点の増加に対する相対L2誤差の向上感度が鈍感。⓷と⓹は類似の挙動をとる。コロケーション点が1,000を越えてから急速に、敏感になる。対照的に、⓺はコロケーション点の数が少ない状況で敏感で、1,000を越えてから鈍感になる。⓵⓸は評価対象外。
③~⑥→ 相対L2誤差の水準は、良くて、③で10-2、④で100、⑤で10-3、⑥で10-32。⓵⓶は、再サンプリング回数を増やしても相対L2誤差が改善しない。④は、壊滅的に精度が低いが、⓺が最良であることに変わりはない。⓺が最良である傾向は、⑤で顕著。⓸は、なぜか評価対象外。
⑦~⑧→ 相対L2誤差の水準は、⑦で10-4に達している。⑧では、10-1に留まる(物理パラメータの影響大)。ここでも、⓺が最良である。
⑨~⑩→ ⑨~⑩における相対L2誤差の水準議論は、本質的に⑦~⑧と同じであるので省略。ここでも、⓺が最も優れた性能を示している。
⑪→ 相対L2誤差の水準は、10-2程度である。⓵⓶は全くダメである。加えて⓵⓶は、再サンプル回数を増やしても、相対L2誤差は全く改善しない。ここでは、⓺の性能は最良とは言えず、代わりに⓸が最良となる。なお⑫及び⑬に関しては、結果が明示されていないが、⑪と同じ傾向であると記されている。
(3) 小括
バーカース方程式の範疇では、色々いじってみても、⓺が最も優れている。しかし、アレン=カーン方程式になると、⓸が最良と言える。ただ、再サンプリング回数が30を越えて以降は、ほぼ最良と考えても良いように思う。つまり、全ての組み合わせで⓺が最も優れている、と言っても良いように思える。[*88]も、そのように結論付けている。
【7】考察と感想
(1) [*87]の考察等
1⃣ 本質的に重要な点は、確率分布に従ってサンプリングすることでコロケーション点を"間接的に"構成するのではなく、”直接”構成するという新しい方法論を示したことであろう。その上で、学習が安定していることを示した。”物理パラメータの広い範囲で、相対L2誤差が小さい”ことは、代理モデルとしては、肝であろう。学習が安定しているとは、物理系及び物理パラメータの『広い範囲』で、相対L2誤差が小さい、ことを指している。安定化のメカニズムは、カリキュラム学習のそれと同様と考えられるだろう。
2⃣ オプティマイザの影響は、やはり大きい。[*87]の結果だけを見ると、LBFGS単体は、ありえない。Adamを第一選択として良いが、多くの場合でAdam+LBFGSを採用することより、精度向上が期待できる。
3⃣ PINNsの相対L2誤差の相場感は、良くて10-4~10-3であることがわかる。
4⃣ [*87]の方法と、エネルギー自然勾配法と組み合わせて、幅広いケースでシミュレーションした結果が見たい。
5⃣ 数値計算でも、気を遣う点というか工夫する点は多々ある。代理モデルの構築においても、それは変わらないと諦念すれば、面倒には思えないかもしれない。もっとも、ツール化されれば、手間ではないだろう。
(2) [*88]の感想
1⃣ [*88]は、問題の根っこを特定して、解決したという内容ではない。対照的に[*87]は、(真実か否かは分からないが)問題の根っこを特定して、解決したという内容である。肚に落ちるし、汎用性が高いと感じる。
70種類を越えるとされる認知症の中で、最も大きな割合を占めるとされているのが、アルツハイマー型認知症(以下、アルツハイマー病)である†1。アルツハイマー病の発症原因は、完全には解明されていないが、アミロイドβ(ベータ)並びに、タウ・タンパク質(以下、タウと略す)が大きな役割を果たしていると、強く信じられている🛡。タウが発症に関わるとされる疾患†2では、その濃度が脳の特定部位で過剰になり、ミス・フォールドしたタウが積み重なって、神経原線維変化(neurofibrillary tangles; NFT)を形成する。このミス・フォールドしたタウの時空間パターンは、タウ濃度を変数とする反応拡散方程式に従うことが、示唆されている。
米ブラウン大学と米スタンフォード大学の研究者は、「PINNsとシンボリック回帰を使って、アルツハイマー病の早期診断モデルを構築した」とする論文[*93](以下、本論文)を発表した(23年7月16日@arXiv)☛【2】(0)を参照。
†1 67.6%という数字が示されることが多い。出典は、[*94]。ただ、これはデータが古い(平成24年。しかし、令和元年の厚生労働省資料[*95]にも引用されている)し、面接調査で診断が確定した”わずか”978 名の内訳に過ぎない。もう少し新しく、患者数も多い(23,484名)調査だと58%という数字がある[*96]。いずれにしても、太宗を占めること自体に、変わりはなさそうである。ただし、若年性認知症では、脳血管性認知症の割合の方が高い[*97]。
†2 タウオパチーと呼ばれる。
🛡 アミロイドβがアルツハイマー病の原因であることを示唆した2006年の論文@natureの撤回について、同意がなされた(24年6月4日[*101])。画像データが改竄されていたためである。脳からアミロイドβを除去することで、アルツハイマー病の症状を改善しようとする試みは、ほぼ全て失敗した(エーザイの「レカネマブ」が唯一の例外)。「アミロイドβがアルツハイマー病を引き起こす」という有力な仮説に対する疑問への、新たな裏付けとなるかもしれない。
【1】本論文の主張
本論文は、以下を主張する:PINNsとシンボリック回帰を組み合わせることで、アルツハイマー病における、ミス・フォールドしたタウ濃度を説明する、反応拡散方程式を発見できる。
【2】事前整理
(0) 本論文でやっていることの事前整理
1⃣ PINNsによる反応モデルの推論
PET画像は、脳内のミス・フォールドしたタウの濃度を抽出し、追跡することを可能にする。 本論文では、ADNI†3データベースから抽出した、被験者76名のタウ濃度データを用いる。タウ濃度が従う方程式(支配方程式)を損失関数に埋め込むPINNsを使って、タウ濃度と反応モデルを、ニューラルネットワーク(NN)で近似する。反応モデルとは、反応拡散方程式の”反応項”を指している。本論文では、反応モデル(反応項)に対して、関数形を仮定せずに、推定する(NNで近似する)。形式上、2種類の物理量をNNで近似していることに注意。
2⃣ シンボリック回帰による表現式の推論
NNで近似された反応モデルに対して、シンボリック回帰を適用して、タウ濃度に関する表現式(関数)を推定する。この関数が異なることをもって、母集団をアルツハイマー病患者と健常対照群とに分別する。
†3 ADNI(Alzheimer’s Disease Neuroimaging Initiative)は、アルツハイマー病発症過程を縦断する脳画像研究[*98]であり、日本、米国、欧州、豪州において、同一プロトコルを用いて実施される、非ランダム化長期観察研究である。2005年に米国で発案、開始された[*99]。日本のADNIは、J-ADNIと呼ばれる。
(1) タンパク質のミス・フォールディングと神経変性疾患の発症
細胞内の小器官リボゾーム(リボソーム)で翻訳・合成されたタンパク質は、アミノ酸が直線状に繋がったひも状の構造をしている。折りたたまれるのは、小胞体においてである。折りたたまれること(フォールディング)によって、ネイティブ構造と呼ばれる固有の立体構造を得る。フォールディングによって、タンパク質は、固有の機能を正しく獲得する。
正しくフォールディングできない、あるいは、正しくフォールディングしたあとで変性することを、ミス・フォールディングと呼ぶ。ミス・フォールディングしたタンパク質は、期待される役割を果たさないので、不要物(言葉を選ばなければ、ゴミ)である。本来、不要物であるミス・フォールディングしたタンパク質は、酵素によって分解されるが、分解機構が何らかの理由で破綻すると、不要物が凝集・蓄積する。そして、凝集・蓄積した不要物は、細胞死を引き起こし、神経変性疾患を発症する†4。
つまり、タンパク質がミス・フォールディングしただけでは、発症しない。排泄する仕組みが破綻して初めて、発症する(はずである。単に処理能力を越えるだけという解釈も可能だろうが、おそらく、それほど単純ではないはず。ただし、本稿は、そこには立ち入らない)。
†4 生体内の不要物は、機能を果たさないだけで留まれば良いが、なぜか悪さをする。
(2) シンボリック回帰
一般に、データから関数を推測することをシンボリック回帰と呼ぶ。シンボリック回帰では、一方で加減乗除を用意し、他方で解析関数を用意する。それらをランダムに組み合わせることで、データの入出力関係に適合する関数を見つける(もちろん"関数"は、入力変数のn次多項式を含む)。アルゴリズムとしては、遺伝的アルゴリズムやニューラルネットワークが使用される。
【3】本論文におけるセットアップ
(0) 2つのステップが必要である理由
本論文は、アルツハイマー病の早期診断モデルを構築する。早期診断とは、アルツハイマー病患者と健常対照群を分別することを指している。分別は、ミス・フォールドしたタウの濃度を記述する表現式が異なることを根拠として、行う。表現式は、二つのステップを経て、推論する。1⃣第一ステップでPINNsを使い、2⃣第二ステップでシンボリック回帰を使う。
なぜ、2つのステップが必要かというと、 陽電子放出断層撮影(Positron Emission Tomography:PET)画像は、高い空間分解能を持っている反面、時間分解能は低く、時間内の数点のみに限定されているからである。つまり、時間的情報が疎ら過ぎるため、PET画像から抽出したタウ濃度から直接、シンボリック回帰によって、表現式を推測することはできない。
(1) グラフ上で離散化した反応拡散方程式
脳のコネクトーム†5におけるミス・フォールドしたタウの凝集と伝播を、反応拡散方程式で表す。反応拡散方程式は、次のような形をした偏微分方程式である。
∂c/∂t=拡散係数∆c+f(c)
この偏微分方程式をPINNsで扱えるように、重み付き無向グラフG上で離散化する。この場合のグラフ(脳グラフ)Gのノードは、重複しない異なる脳領域を、エッジは、異なる領域間の軸索†6接続を表す。具体的な脳グラフは、ブダペスト・リファレンス・コネクトームv3.0†7から、取得する。オリジナルの脳グラフには、1,015個のノードがあるが、これを83個の縮小させた。この83個のノードは、83 個の皮質および皮質下の脳領域と考えられる。
離散化した支配方程式は、以下のようになる(ここにオリジナリティはない)。
dci/dt=-κ∑jLijcj+αf(ci)
ciは、領域iのタウ濃度。κは拡散係数、αは反応係数。Lijは、グラフ・ラプラシアン†8である。i及びjは、全てのノードに渡る(つまり、本論文では1~83)。PINN 推論段階で10回の独立したシミュレーションを実行して、被験者ごとに10 個の異なる「パラメーター セット{κ、α}及び反応モデルf」、を取得する。
†5 神経系内各要素間の詳細な接続状態を表した”地図”をコネクトームと呼ぶ。
†6 (神経)軸索は、神経細胞の細胞体から延びる突起状の構造を有し、他神経細胞への情報の出力を担う。
†7 ブダペスト・リファレンス・コネクトーム・ヴァージョン3.0は、477人のコネクトームから得られたパラメータ化可能な(コンセンサス)脳グラフ。477人のコネクトームは、ヒューマン・コネクトーム・プロジェクトのMRIデータセットから計算された。脳グラフは、サイト(https://pitgroup.org/connectome/)からダウンロードできる。
†8 グラフ・ラプラシアンL=次数行列Dー隣接行列A、である。
(2) 損失関数
本論文のPINNsでは、損失関数は、データ損失+PDE損失+補助損失、で構成される(初期損失・境界損失はハード制約されるので、最適化計算の対象たる損失関数には現れない)。本論文の支配方程式である反応拡散方程式は、拡散項と反応項で構成される。拡散項は既知(パラメータは未知)、反応項は未知である。従って、このケースはPINNsの文脈で言うと、形式上、逆問題と見做すことができる(だろう)。従って、 データ損失が考慮されているという解釈が可能である(と思われる)。
また補助損失(正則化項)は、反応拡散方程式は進行波解を持つことを保証する条件を、ソフト制約として課す役目を果たしている。
なお、オプティマイザはAdam+L-BFGSが使用されている。
(3) シンボリック回帰
1⃣ 概要
本論文では、(本論文の著者の一人が所属する)米スタンフォード大学が開発したPySRが使用されている†9。PySRは、Juliaバックエンド SymbolicRegression.jl上に構築されたPythonインターフェイスを備えたオープンソース・ソフトウェアである。PySRは、遺伝的アルゴリズム・ベースのシンボリック回帰である(ほとんどが、そうであると言っても良い)。
2⃣ 評価方法及び、評価指標
シンボリック回帰から発見された式(以下、表現式とする)を評価する指標として、スコア=-δlog(MAE)/δℭが使用された。MAEは平均絶対誤差、ℭは式の複雑さを表す。δは局所的な変化を表している†10。
損失が少なくスコアが高いモデルが好ましいので、損失とスコアのバランスをとる。具体的には、損失については、最小値の5割増しまでを許容範囲する。つまり、損失最小のモデルにおける損失を1.5倍した値より、損失が大きくないモデルは候補として残す。この時点で「パラメータ{κ、α}及び表現式」のセットが残る。
次に、表現式を一つに絞り込むため、射影誤差という指標を導入する。射影誤差は、本質的に||実際のタウ濃度c(t)ー推定タウ濃度c'(t)||2で表される(ノルムはL2ノルム)。c'(t)は、表現式を反応項として代入した反応拡散方程式の解である†11。射影誤差が最小の表現式が、最終的に選ばれる。
†9 シンボリック回帰(SR)用ツールには、他にも、SINDy、Eureqa、AI Feynman、AI-Descartes等がある(まだまだ沢山ある)。なお、23年7月@arXivの論文[*100]は、「実世界のデータでしばしば直面する一般的な課題に対して、SRがどの程度有効であるかを評価するために、合成データセットと実世界のデータセットからなるコンペティションを開催した」結果をまとめた論文である。唯一無二のツールはない、というのが結論である。ただ、ざっくり言って、PySRは優秀な成績を修めていると思う。
†10 本論文では、∆という記号が使われているが、ラプラシアン(∇2)と紛らわしいので、δを使った。
†11 グラフ上で離散化した反応拡散方程式(常微分方程式)は、scipy.integrate.odeintを使って解いた。
【4】結果
(0) 予備テスト
1⃣ セットアップ
まず、PINNs+シンボリック回帰が、ミスフォールドしたタウ濃度を表現する式を構築できるか、についてテストを行った。具体的には、初期条件・パラメータ・反応項を変化させた、タウ濃度のシミュレーションが実行された。
i 番目のノード(すなわち脳領域)の初期タウ濃度(初期条件)は、実際のデータと同等の平均と分散を持つ正規分布からサンプリングされた。パラメータκ及びαは、適当な平均と分散を持つ正規分布に従うと仮定された。被験者は、4グループに分けられ、それぞれ異なる反応モデル:Fisherモデル(①c(1 − c))、Newell-Whitehead-Segelモデル2種(②3√3c(1ーc2)/8、③22/3c(1ーc3)/3)、Zeldovich-Frank-Kamenetskiiモデル (④(2+√5)c(1ーc)exp(cー1ー(ー3+√5)/2)/4)、が割り当てられた。グラフ・ラプラシアンは、実際のデータと同一になるように設定された。タウ濃度c(tk)は、k = 0、1、2 年に対して、 tk = k でサンプリングされる。
最後に、パラメーター κ と α およびは反応モデルを特定した後、それらをグラフ上で離散化した反応拡散方程式(常微分方程式)に代入し、scipy.integrate.odeintを使用して解いた(期間は20年)。そうすることで、モデルの予測可能性を調べた。
2⃣ テストの結果
4パターンの反応モデルをシンボリック回帰した結果は、ほぼ正確である。①は、c(1 − c)が、(1ー0.01c)×c(1ーc)とシンボリック回帰された。つまり1→1ー0.01cである。②は、3√3c(1ーc2)/8が、0.65c(1ーc2)である。つまり、3√3/8≒0.6495→0.65である。③は、22/3c(1ーc3)/3が、0.53c(1ー1.019c3)である(1.019は、概数値)。つまり、22/3/3≒0.529→0.53、かつ1→1.019(=54/53)である。④は、(2+√5)c(1ーc)exp(cー1ー(ー3+√5)/2)/4が0.58c(1ーc)exp(c)である。つまり、(2+√5)exp(ー1ー(ー3+√5)/2)/4≒0.5708→0.58である。
最終的なタウ濃度の予測結果(反応拡散方程式を解いた結果)†12とグランドトルゥースとの比較は、図示されているのみである。図を見る限り、一致精度は高い。
†12 嗅内皮質、中側頭回、上側頭回という3つの異なる脳領域において行われた。正確には、それぞれ左と右があるので、6つの領域ということになる。嗅内皮質は、海馬と共に記憶に深く関わる脳領域とされる。側頭葉を構成する頭回の一つである中側頭回は、視聴覚情報の統合を担っていると考えられている。(同様な)上側頭回は、聴覚を担うとされる(一次聴覚野がある)。
(1) 実データによる結果
76 人の被験者は 2 つのグループに分類された。46 人は、平均アミロイド濃度が一定レベルを超えることを意味する、アミロイド陽性(Aβ+)として識別され、30 人はアミロイド陰性 (Aβ-) として識別される。
Aβ+=アルツハイマー病患者の反応モデルf+(c)は、 f+(c) = 0.23c3−1.34c2+1.11cと推定された。Aβ-=健常者の反応モデルf-(c)は、f-(c) = −c3 + 0.62c2 + 0.39cと推定された。図で表すと、f+(c)は、タウ濃度が薄い段階で(つまり早い段階で)立ち上がっていることがわかる(これは、アルツハイマー病患者は、タウ濃度が低い段階で、タウのミス・フォールディングが発生していると捉えて良いのだろうか?)いずれにしても、f+(c)とf-(c)は識別できる(と見做して良いだろう)。
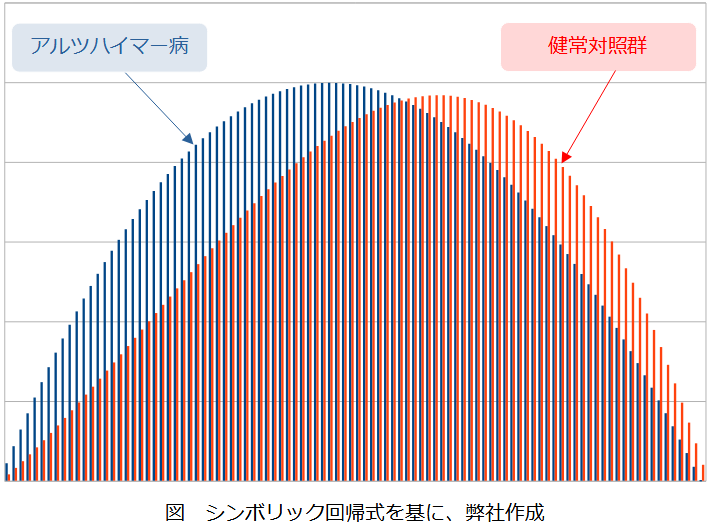
それぞれの反応モデルを代入した(グラフ上で離散化された)反応拡散方程式を解いた。期間は30年。
(テストデータと同様に)被験者36人がランダムに抽出された。脳領域も同様に、嗅内皮質、中側頭回、上側頭回という3つの領域が対象である。さらに左右の区別があるので、正確には、6つの領域が対象となっている。実データの場合は、PINNs+シンボリック回帰の結果が、どれほどバラついているかを図示している。つまり、予測結果の「最大値・最小値及び、最良値」を30年間にわたり図示している。おおむね5/6は、バラつきが小さい(安定した予測ができている?)と見做せるだろう。
【5】考察
(0) Fisherモデルは別として、Newell-Whitehead-Segelモデル、Zeldovich-Frank-Kamenetskiiモデルは、そこそこ複雑な形をしているが、シンボリック回帰は見事に成功している。
(1) PINNsの新しい可能性が示されたのかもしれない。データが少ないあるいはノイズが大きいため、直接的にはシンボリック回帰が適用できないケースでも、PINNsを併用することでシンボリック回帰可能であれば、新しい機会が生まれる。説明可能な深層学習フレームワークが望まれる時世なので、今後適用例が増えるかもしれない。
(2) 本論文では、偏微分方程式(反応拡散方程式)をグラフ上で離散化した常微分方程式(系)を埋め込んだPINNsを使用している。ブダペスト・リファレンス・コネクトームを使って、脳グラフを利用できるため、実行可能なフレームワークである。数理的には、シグネチャや圏論を使った解析も可能であろう(が、特段のメリットは無いかもしれない)。
チリのマヨール大学・米ハーバード大学他の研究者は、「PINNsは量子最適制御において、優れた性能を発揮する」と主張する論文(以下、本論文[*89])を発表した(23年12月7日@arXiv)。最適制御にニューラルネットワークを適用するというアプローチは、古典の範疇でも比較的新しい。
本論文では、量子コンピュータへの適用を念頭に、量子最適制御を議論している(ことが本論文のSUPPLEMENTAL MATERIALを見ると、分かる)。
【1】本論文の主張
本論文は、少数自由度の開放量子系を対象とした、PINNsによる量子最適制御は、以下の通りである主張する。
(1) 量子状態の遷移(分布の移動)を、低エネルギー消費、短時間、かつ高忠実度で達成する。
(2) 学習パラメーターが変更された場合に堅牢であり、標準的な方法と比較してより良い結果を提供する。
【2】事前整理
(0) 最適制御とは何か?
本論文は、最適量子制御を扱った論文である。最適量子制御は、最適制御の量子版という意味になる。それでは、最適制御とは何か。最適制御(問題)をより一般的に定義すると、「制御目的を表す量を最小にするような制御入力(操作量)を求める」問題となる [*90]。工学的に具体的な制御目的を表す量には、時間や距離、エネルギー消費量などがある。やや狭く定義すると、「初期状態と目的状態が与えられた時、初期状態を目的状態に駆動する制御外場(制御入力)を設計する」問題となる。量子系において、このような制御外場の存在は、特定条件下で保証されているようである[*91]。
制御入力に対する最適性条件は、多くの場合、手計算では解けない(解析解を求めることが、一般的には不可能)。さらに、計算コストから数値計算でも難しいと考えられてきた。そうなると、機械学習・深層学習の出番となる。ただ、最適制御問題に深層学習を適用するというアプローチは、古典の範疇でも、まだ新しいようである(例えば、2021年11月の研究[*92])。
(1) そもそも論-本論文でPINNsは、何をやっているのか
本論文が、何をやっているかを、以下説明する。本論文における量子制御とは・・・を説明する前に、まずは、概要を掴もう。そのために、自然に存在している量子系を人工の量子系で模して、人工的に制御することを考えよう。例えば、人工原子で量子ビットを作成し、量子ビットを制御して量子計算を行うこと(量子コンピュータ)をイメージすると、分かり易いだろう。その場合、レーザー光やマイクロ波パルスを照射して、量子ビットを制御する。PINNs寄りの言葉を使うと、量子ビットを所望の状態に変化させるパラメータ((0)で現れた文言を使うと、制御入力)を見つけることが、本論文におけるPINNsの目的である。
さらに言うと、本論文の問題設定は、逆問題(かつ外挿問題)に相当する。そして蛇足ながら、初期値問題ではあるが、境界値問題ではない。
(2) 本論文における量子制御とは・・・
詳しい内容を把握するため、量子物理に戻ろう。唐突だが、本論文が扱う対象は、少数自由度の弱結合開放量子系である。この設定のお陰で、密度演算子の時間発展は、微分方程式(量子マスター方程式)で記述可能となる。少数自由度として本論文では、具体的には、2準位系~4準位系が登場する。
本論文における量子制御とは、基底状態|g⟩と励起状態|e⟩の量子遷移を制御する、という意味である。これを制御系dx(t)/dt=A・x(t)として見た場合、状態変数(ベクトル)x(t)は、密度演算子と|g⟩及び|e⟩から構成できる。有体に言えば、x(t)は、密度行列の要素ρij=⟨i|ρ(t)|j⟩である。ここで、|i⟩は、|g⟩もしくは|e⟩である。密度行列の対角要素ρiiは、|i⟩から|i⟩の遷移確率(つまり、|i⟩に留まる確率)を表し、非対角要素ρijは、|i⟩と|j⟩の位相関係(コヒーレンス)を表す。ダイナミクスを記述する行列Aの行列要素は、パラメータ(制御理論の文脈では、制御パラメータあるいは制御変数と呼ばれる)を含んでいる。
密度演算子は適当な初期値を与えると、 量子マスター方程式の解として得られる。深層学習・ニューラルネットワーク(NN)寄りの表現を使うと、本論文では状態変数x(t)は、量子マスター方程式を介して密度演算子から「生成される」。従って、本論文のNN(正確には、PINNs)は、データ・フリーで学習される。dx(t)/dtは、(Pytorchパッケージの)自動微分を使って計算される。
(3) 損失関数
本論文における損失関数Lは、次のように4つの項の和で表される。L=Lmodel+Lcontrol+Lconst+Lreg。一般的なPINNsの文脈で言うと、LmodelはPDE損失で、Lcontrolは、データ損失である。Lconstは、支配方程式とは異なる物理法則に関する(ソフト)制約に関する項目である。流体解析を例にとると、連続の式(質量保存則)を満たすように構成した損失関数が該当する。本論文では、4準位系の取り扱いにおいて、登場する。最後のLregは、正則化項である。
逆問題なので、データ損失に相当するLcontrolが含まれている。なお、初期損失は(デフォルトでは)ハード制約のため、最適化計算には含まれていない。補足情報で、ソフト制約とした場合との比較がなされている†1。
†1 初期損失Licを追加した損失関数をL’とする:L’=L+λLic。λが小さい(λ=1)の場合は、ハード制約(つまり損失関数がL)とソフト制約(つまり損失関数がL’)に対する「制御入力と量子忠実度の時間挙動、ダイナミクス」に関して、違いがほぼない。ただし、λを大きくすると、L’の収束性が低下する。
【3】本論文で行っていること
(0) 前捌き
少数自由度の弱結合開放量子系を扱っている本論文では、2準位系、3準位系、4準位系に対して、量子最適制御を適用している。ただし、2準位系は定性的に取り扱われているに過ぎない。4準位系は、本文では一言触れられているだけである(SUPPLEMENTAL MATERIALで、定性的に取り扱われている)。定量的に取り扱われているのは、3準位系のみである。
(1) 2準位系のセットアップ
2準位系は、基底状態|g⟩と励起状態|e⟩があり、|e⟩に制御入力(制御外場)を作用させる制御系として設定されている。|g⟩は、電磁波を吸収して|e⟩に遷移する。|e⟩は、電磁波を放出して|g⟩に遷移する。適当な初期(定常)状態、目的(定常)状態、及び物理パラメータを設定し、解析的に最適化された結果とPINNsを使って最適化された結果を比べて、後者が優れているとする。優れているの意味が明示されていないが、合理的に推測すると、目的定常状態に達するまでの時間が、より短いという意味であろう。
具体的な初期(定常)状態は、0.2775 |e⟩⟨e| + 0.7225|g⟩⟨g| + [(−0.1106 + i0.0083)|g⟩⟨e| + c.c.]、目的(定常)状態は、(1/2)(|e⟩⟨e|+|g⟩⟨g|)とされている(c.c.は複素共役)。PINNsの結果は、忠実度0.99である。
(2) 3準位系のセットアップ
1⃣ 概要
3準位系の例は、2準位系の例と異なり、具体的でイメージし易い。3準位系の制御目的は、損失のある中間状態|3⟩を介して、初期状態|1⟩から、目的状態 |2⟩に分布(原語ではpopulation)を効率的に移動するための、最適な制御外場Ωp(t)およびΩs(t)を見つけることである(標準的な最適制御問題の設定)。Ωp(t)とΩs(t)は、制御外場のラビ周波数であるが、制御外場のラベルとしても使用している。
Ωp(t)は|1⟩⇆|3⟩に、Ωs(t)は|3⟩⇆|2⟩に携わる。下付き添え字pはポンプ光を、添え字sはストークス光を意味している。また、Ωp(t)及びΩs(t)は、<10と制限されている。
2⃣ 制御目標
制御目標 は、㊀|3⟩の分布を最小にすること、㊁エネルギー消費量(制御外場の作用)を最小化すること、である。㊀の定量化は、p2=Tr[ρσ22]で行われている。つまり22=|2⟩⟨2|の期待値である。|1⟩から|2⟩への分布移動において、中間状態|3⟩の残存を最小化することは、忠実度が高い(高忠実度)、と表現されている。
㊁の定量化は、Ā=∫(|Ωp(t)|2+|Ωs(t)|2)1/2dtで行う(注:本論文で使われてる記号はĀ ではない)。Āは、tについて、0から分布の移動時間tfまで積分する。tfは、最も高い確率の目的状態に到達するのに必要な時間として定義される。
3⃣ 他の制御手段との比較
❶PINNsは、4つの他制御手段(❷STIRAP†2、❸STIREP†3、❹インバース・エンジニアリング†4、❺MOD-SATD†5)と比較されている。
㊀は、❶0.97、❷0.98、❸0.98、❹0.97、❺0.98である。㊁は、❶7.3❷128.6、❸53.3、❹19.8、❺50.0である。分布の移動時間tfは、❶2.0、❷35.0、❸9.4、❹3.0、❺13.0である(単位は、任意単位a.u.)。なお、 Ā/tfは、❶3.65、❷3.67、❸5.67、❹6.60、❺3.57である。
4⃣ 評価
PINNsによる制御は、㊀において特に優れていないが、㊁において優れている。これは主に、tfの短さがもたらしているものと考えられる。
また、PINNsが学習パラメータの変更に堅牢であるとされている。これは2光子による離調(detuning)δが、STIRAPには悪影響を及ぼす(δが増加するとSTIRAPが劣化する)一方で、PINNsによる制御には悪影響を及ぼさないことを意味しているようである。またδ≠0の場合の、他の制御手段の最適化は自明ではないそうである。
まとめると、本論文では、次のように主張されている:PINNSは㈠低エネルギー消費かつ短時間で、高い忠実度を達成する。㈡学習パラメーターが変更された場合に堅牢であり、標準的な方法と比較してより良い結果を提供する。
†2 誘導ラマン断熱過程(STImulated Raman Adiabatic Passage)。STIRAPは断熱時間発展に従うので、遅い。STIREP、インバース・エンジニアリング、MOD-SATDは、全て時間を短縮するための改善を施した代替手法、と考えてよい。なお、SUPPLEMENTAL MATERIALには、断熱ショートカットを使って高速化したSTIRAPも取り上げられている。
†3 誘導ラマンexact過程(STImulated Raman Exact Passage)。インバース・エンジニアリングの手法を取り込むことで高速化を計っているらしい。
†4 時間依存の補助パラメータを”上手く”導入するところがミソらしい。Ωp(t)とΩs(t)は、補助パラメータを使って表現される。補助パラメータを求める方が速ければ、結果的に、より速くΩp(t)とΩs(t)を見つけることができる。
†5 断熱性による損失の影響を打ち消しながら、断熱条件を回避する、別の代替手段らしい。
(3) 4準位系のセットアップ
4 準位系には、より多くの非線形方程式が含まれており、新しく追加された状態へのクロストークの可能性が含まれる。つまり、4 準位系への拡張は簡単ではない。4 準位系に対する本論文の主張は、「PINNsがネットワーク・アーキテクチャを変更せずに 4準位系を処理できる」である。具体的には、損失関数に、新しい項 Lconstを追加するだけである。
4準位系の制御目標は、⓵損失のある中間状態(|3⟩)の分布を最小化し、⓶エネルギー消費を最小化し、⓷状態|4⟩ へのクロストークを最小限に抑えて、状態|1⟩から状態|2⟩ への分布移動に成功する PINN を学習することである。⓷は選択性を保証するものであり、3準位系には必要ない。
PINNsによる制御の結果、適当な定常状態に到達することが、(図11)に示されている。
(4) ハイパーパラメータ等†6
オプティマイザー・・・Adam
活性化関数・・・正弦関数(sin)
隠れ層の数・・・4、5、5
エポック数・・・4、2、2(全て、×104)
ニューロン数・・・200、150、150
学習率・・・0.1、8.0、8.0(全て、×10-3)
η†7・・・0.1†8、0.2、0.2
χ†9・・・1.0、2.8、2.8(全て、×10-3)
†6 3つの数値が記載されている場合は、順番に、2準位系、3準位系、4準位系に対する数値である。
†7 Lcontrol(データ損失)にかかる重みである。
†8 SUPPLEMENTAL MATERIALの表Ⅱでは0.1。本文図3では1となっているが、0.1の誤植と思われる(0.1の方が、整合的である)。
†9 Lreg(正則化項)にかかる重みである。
【4】考察
(1) (量子、古典は別として)最適制御は難しい。なぜPINNsで上手く行ったのか。仮に、「最適制御問題は、ニューラルネットワークから見ると、単に逆問題(かつ外挿問題)に過ぎない」と整理できれば、PINNsで上手く言っても不思議ではない。この仮に・・・を是とすれば、(古典)最適制御でもPINNsは有効に機能するはずである➡ 人工衛星の軌道推定に関する論文[*85](こちらを参照)は、PINNsを(古典)最適制御に適用した論文と見做すことができるかもしれない。もちろん、[*85]でPINNsは有効に機能している。
(2) もちろん「PINNsは、最適制御問題を簡単に解ける!」は安直過ぎる。そんなことはないだろう。PINNsの学習は、実は難しい(と言われている)。本論文でなぜ上手く言っていったのか、をテクニカルに考えると、以下のことが言えるかもしれない。
1⃣ 損失関数に多数の項目を詰め込めるから。実際、4準位系では、第二のPDE損失(項)と考えられるLconstを導入することで、安定的な学習ができた、としている。
2⃣ 他事例では、ほぼ現れない正則化項が導入されている。
3⃣ 量子マスター方程式の解を使ってPINNs学習を進めるから、自然に、初期値を与える点から徐々にコロケーション点が拡大するという流れになっている(そもそも、初期値問題ではあるが境界値問題ではないので、コロケーション点の構成に(再)サンプリングを用いるというアプローチは、ない)。コロケーション点を規律に従って徐々に増やすという手法は、別稿で示した通り、安定性には寄与するはずである。
(3) 正則化項含めて、損失関数の重みは、試行錯誤的に決めるしかない(コロケーション点の数が与えられるわけではないから)。試行錯誤的に決定するのは、面倒だったろうが、量子コンピュータ(量子ビット)の制御なら十分ペイするのだろう(リアルタイム制御が可能かは分からないが・・・)。
(4) 学習パラメータの変更に対する堅牢性は、量子コンピュータへの応用を見据えた上で、貴重な特徴と言えるだろう。
【尾注】
(*40 Sifan Wang et al.、AN EXPERT’S GUIDE TO TRAINING PHYSICS-INFORMED NEURAL NETWORKS、https://arxiv.org/pdf/2308.08468.pdf)
(*74 Zhongkai Hao et al.、PINNACLE: A COMPREHENSIVE BENCHMARK OF PHYSICS-INFORMED NEURAL NETWORKS FOR SOLVING PDES、https://arxiv.org/pdf/2306.08827.pdf)
*85 Jacob Varey et al.、Physics-Informed Neural Networks for Satellite State Estimation、https://arxiv.org/pdf/2403.19736.pdf
*86 超伝導方式の量子コンピュータを開発しているフィンランドのスタートアップ「IQM quantum Computers」は、アールト大学とVTT(フィンランド国立技術研究センター)のスピンアウト・スタートアップである。
*87 Katsiaryna Haitsiukevich & Alexander Ilin、IMPROVED TRAINING OF PHYSICS-INFORMED NEURAL NETWORKS WITH MODEL ENSEMBLES、https://arxiv.org/pdf/2204.05108.pdf
*88 Jose Florido et al.、Investigating Guiding Information for Adaptive Collocation Point Sampling in PINNs、https://arxiv.org/pdf/2404.12282)
*89 Ariel Norambuena et al.、Physics-informed neural networks for quantum control、https://arxiv.org/pdf/2206.06287
*90 大塚智之、最適制御の考え方と最近の展開、2016年7月4日、https://www.usss.kyoto-u.ac.jp/wp-content/uploads/2021/03/20160704_Ohtsuka.pdf
*91 孤立スペクトルを持つ系は完全制御可能であるという結果から、導かれる。出所:高見利也・藤崎弘士・宮寺隆之、粗視化描像における量子カオス制御、https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1369-3.pdf
*92 https://www.nii.ac.jp/news/release/2021/1104.html
*93 Zhen Zhang et al.、Discovering a reaction-diffusion model for Alzheimer’s disease by
combining PINNs with symbolic regression、https://arxiv.org/pdf/2307.08107
*94 厚生労働科学研究費補助金(認知症対策総合研究事業)総合研究報告書「都市部における認知症有病率と認知症の生活機能障害への対応、H24総合報告書_Part3(http://www.tsukuba-psychiatry.com/wp-content/uploads/2013/06/H24Report_Part3.pdf)の図9。
*95 厚生労働省老健局、認知症施策の総合的な推進について(参考資料)、令和元年6月20日、https://www.mhlw.go.jp/content/12300000/000519620.pdf
*96 https://www.tmghig.jp/research/topics/201703-3382/
*97 https://www.mhlw.go.jp/houdou/2009/03/h0319-2.html ただし、こちらはさらにデータが古く、発表が平成21年、調査は平成18年度~20年度である。
*98 岩坪威、ヒト脳疾患画像データベース統合化研究、https://biosciencedbc.jp/gadget/rdprog_over/iwatsubo.pdf
*99 荒井 啓行、アルツハイマー病の発症前診断と MCI、https://www.jstage.jst.go.jp/article/clinicalneurol/49/11/49_11_838/_pdf
*100 F. O. de Franca et al.、Interpretable Symbolic Regression for Data Science:Analysis of the 2022 Competition、https://arxiv.org/pdf/2304.01117
*101 https://www.science.org/content/article/researchers-plan-retract-landmark-alzheimers-paper-containing-doctored-images

