補足資料 for PINNs
ケンブリッジ大学[*1]の研究者は、「PINNsは、有限要素法に勝てない」と主張する論文[*2](以下、本論文)を発表した(23年2月8日)。言及されているPINNsは、プレーン・バニラなPINNsである。勝てない、の詳細については【1】を参照。以下では、プレーン・バニラなPINNsを対象としていることについて述べる。
プレーン・バニラなPINNsを比較対象とすることには、あまり意味はないと思われる。機械学習・深層学習モデルには、「あらゆる問題に対して、良い性能を示すような万能モデルは、存在しない」ことが知られている(ノーフリーランチ定理と呼ばれる)。ニューラルネットワークは、その柔軟性に最大の特徴があり、その柔軟性故に、多くのバリアント(派生種)が生まれている。各バリアントは、特定タスクに対して、それぞれの強みを持っている。
これは、PINNsも同様である。プレーン・バニラなPINNsは、良い結果をもたらさないことがしばしば、ある。そのため、多くのバリアントが開発されている。プレーン・バニラなPINNsを対象としてPINNs全体を評価することは、「プロンプトを工夫せずに、出力された結果でchat-GPTを評価すること」と同程度の意味しかないと考えられる。ただし、PINNsの基礎体力を測るという観点からは、意味があるだろう。
【1】本論文の主張
本論文は、「プレーン・バニラなPINNsは、速度と精度で、有限要素法(FEM)に勝てない」と主張する。
3つの物理方程式(空間次元は、方程式によって、1次元から3次元)を対象として、比較が行われた。速度とは、「計算時間と評価時間†の長短」を意味している。L2相対誤差で計測される精度は、計算と評価それぞれについて算出される。
† 原語は、evaluation time。PINNsの場合は、学習済の代理モデルに対し新たな入力を行い、出力を得るまでの時間として測定される。FEMは、ある固定メッシュ上で解いた偏微分方程式の解を、別のメッシュに内挿することが可能である。つまり、FEMの場合は、別のメッシュに内挿する時間として測定される。
【2】セットアップ
(1) 対象とする物理方程式
1⃣ ポアソン方程式
ポアソン方程式は、2階楕円型線形偏微分方程式である。物理学の様々な場面で、用いられる。ポアソン方程式には解析解が存在するので、解析解をグランドトルゥースとして、L2相対誤差を計算する。本論文では、1次元から3次元までの空間次元を取り扱っている。
2⃣ アレン・カーン方程式
アレン・カーン方程式は、反応拡散系を記述する2階放物型非線形†偏微分方程式である。物理学の文脈では、相分離現象のモデル方程式として使用される。流体力学の文脈では混相流のモデル方程式として使われる。アレン・カーン方程式には、解析解は存在しない。従って、細かいメッシュを使ったFEMで求めた解をグランドトルゥースとして、L2相対誤差を計算する。空間次元は、1次元のみを取り扱っている。
† より正確に言うと、半線形(semi-linear)である。アレンカーン方程式は2階偏微分方程式であるが、非線形性は、2階偏微分項には存在しないため、半線形である。
3⃣ 半線形シュレーディンガー方程式
非線形シュレーディンガー方程式は、2階双曲型非線形偏微分方程式である。この場合の非線形は、半線形である。半線形シュレーディンガー方程式が、どのような物理的場面で扱われるのか、寡聞にして知らない。(本論文で取り上げた)半線形シュレーディンガー方程式には、解析解は存在しない。従って、細かいメッシュを使ったFEMで求めた解をグランドトルゥースとして、L2相対誤差を計算する。空間次元は、1次元及び2次元を取り扱っている。
(2) FEM
物理方程式の解は、パイソン・インターフェースを持つオープンソースのFEMソルバーである FEniCSを用いて求めた。FEMでは、変数関数を基底関数の線形結合で表現する。本論文では、基底関数として、区分線形関数(ハット(hat)関数)を採用している。基底関数として用いられるハット関数は、P1基底†とも呼ばれる。P1基底の採用は、きわめて標準的である。
† 一般に、三角形上で用いられるk次の多項式である基底関数を、Pk基底と呼ぶ。従って、P1基底は三角形上で1次多項式を基底関数として用いる、という意味になる。
(3) PINNs
モデル・アーキテクチャは、全結合のフィードフォワード・ニューラルネットワーク。幅と深さは、各物理方程式に対して、様々なバリエーションが用いられる。活性化関数はtanhを採用している。最適化は、2段階方式で行われた。まずAdamを使い、次にL-BFGSを使う。これは、収束を速めるために、PINNsでは普通に使われる方法である(L-BFGSが、学習開始時直ぐから使用されることは少ない†)。学習率は、物理方程式によって異なるが、1×10-4もしくは、1×10-3を使用している。L-BFGSに切り替えるタイミングも、物理方程式によって異なる。
コロケーション点をサンプリングする手法は、ラテン・ハイパーキューブ・ サンプリング法を採用している。なお、エポックごとにコロケーション点を再サンプリングする。ただし、L-BFGS では再サンプリングが許可されていないため、Adamから切り替えるタイミングで、1 度だけサンプリングする。
ハードウェアは、NVIDIA Quadro P6000 GPUが使用された。ソフトウェア・ライブラリには、JAXが使用された。
† PDE損失項♭1をソフト正則化項♭2とする(プレーンバニラな)PINNsは「精度が悪過ぎて」ほぼ使えないと主張する論文[*3]では、学習の最初からL-BFGSを用いている。(公開が21年11月とやや古い)[*3]では、カリキュラム正則化という手法を使えば、精度(L2相対誤差)が2桁改善すると書かれている。カリキュラム正則化とは、学習が容易なパラメータから学習を始めて徐々にパラメータを大きくしていく、という手法を意味している(名前の由来は、カリキュラム学習)。複雑なことはせず、オプティマイザを「Adamから初めてL-BFGSに移行」とすることで解決するのではないだろうか?
♭1 PINNsの損失関数の内、「支配方程式=0」で構成される損失関数を指している。
♭2 損失関数=重み×PDE損失項+初期損失項+境界損失項、として、損失関数最小化を目指す手法は、ソフトと形容される。損失関数=0を目指すならハードである。先の損失関数では、PDF損失項のみに重みが付いていて、PDE損失項がソフト正則化項となっている。なお、正則化項が加算されているので、左辺は損失関数ではなく、コスト関数と呼ぶ方が正確である。
【3】比較結果
(0) 為念・リマインド
精度は、L2相対誤差で評価される(単位なし)。計算時間と評価時間の単位は、秒である。
(1) ポアソン方程式
1⃣ 1次元ポアソン方程式
境界条件は、ディリクレ条件を使用した。
PINNsのセットアップ:学習率1×10-4。エポック数15,000。隠れ層の数=0,1,2(隠れ層0を設定する必要があるだろうか?)。幅={5、10、20、40}。
㈠ 計算精度・・・PINNsは、層の深さと幅の組み合わせで、10-6~10-1と大きく振れる。FEMは、10-7~10-4である。FEMの方が精度が高い。
㈡ 計算時間・・・PINNsは、101秒のオーダー。一方、FEMは10-2秒 のオーダーであり、およそ3桁程度速いことになる。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である(つまり、FEMの方が高精度)。
㈣ 評価時間・・・PINNsは、10-1秒 のオーダー。FEMは、10-2秒 のオーダー。FEMが10倍位は速い。
2⃣ 2次元ポアソン方程式
境界条件は、混合境界条件(つまりある部分でディリクレ条件、他でノイマン条件)を使用した。
PINNsのセットアップ:学習率1×10-3。エポック数25,000。隠れ層の数=0,1,2,3。幅={20、40、60、120}。
㈠ 計算精度・・・PINNsは、10-2~10-1。FEMは、10-5~10-3である。FEMの方が精度が高い。
㈡ 計算時間・・・PINNsは、102秒のオーダー。一方、FEMは10-1~101秒のオーダーであり、1~3桁程度速いことになる。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である(つまり、FEMの方が高精度)。
㈣ 評価時間・・・PINNsは、10-1秒 のオーダー。FEMは、101秒 のオーダー(計算時間よりも、遅い)。PINNsが2桁程度速い。
3⃣ 3次元ポアソン方程式
境界条件は、ディリクレ条件を使用した。
PINNsのセットアップ:学習率1×10-3。エポック数20,000。隠れ層の数=1,2,3,4。幅={20、60}。
㈠ 計算精度・・・PINNsは、およそ10-3程度。FEMは、10-3~10-2である。PINNsの方が高精度と言っても良いのではないだろうか。
㈡ 計算時間・・・PINNsは、102秒のオーダー。一方、FEMは10-1秒~101秒。1~3桁程度速いことになる。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である。
㈣ 評価時間・・・PINNsは、10-1秒 のオーダー。FEMは、101秒 のオーダー。2次元のケースと同様に、PINNsが2桁程度速い。
(2) アレン・カーン方程式
アレン・カーン方程式は、1次元のみである。境界条件は、周期境界条件を設定(つまりu(t,0)=u(t,1)という形式の境界条件)。
PINNsのセットアップ:学習率1×10-4。エポック数50,000。ただし、最初の7,000 エポックの間は、「初期条件に関する損失関数(初期損失関数)に対してのみ」Adam オプティマイザーを実行した。これは、損失関数全体に対して最適化を実行すると、初期条件を学習するのに苦労したため、である。また、初期損失関数には、重み1,000を掛けた。隠れ層の数=2,3,4,5,6。幅={20、100、500}。
㈠ 計算精度・・・PINNsは、およそ10-1程度。FEMは、上限が10-1程度であり、FEMの方が精度が高い。
㈡ 計算時間・・・PINNsは、103秒~104秒。一方、FEMは10-2秒。FEMが、5~6桁程度速いことになる(相手にならないレベル)。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である(故に、FEMが高精度)。
㈣ 評価時間・・・PINNsは、10-1秒 のオーダー。FEMは、10-3秒。FEMが2桁程度速い。
(3) 半線形シュレーディンガー方程式
1⃣ 1次元
境界条件は、周期境界条件を課した。解は複素数値で、実部と虚部がある。ほぼ同じ結果なので、実部に対してのみ、結果を示す。
PINNsのセットアップ:学習率1×10-4。エポック数50,000。隠れ層の数=2,3,4,5。幅={20、100}。
㈠ 計算精度・・・PINNsは、およそ10-1程度。FEMも10-1程度であるが、PINNsの方が精度が高い。
㈡ 計算時間・・・PINNsは、103秒。一方、FEMは101秒に至らない。FEMが、2桁程度速いことになる。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である(故に、PINNsの方が高精度)。
㈣ 評価時間・・・PINNsは、10-1秒 のオーダー。FEMは、10-2秒に至らない。FEMが1桁程度速い。
2⃣ 2次元
境界条件は、周期境界条件を課した。2次元でも、実部と虚部の結果は、ほぼ同じなので、実部に対してのみ、結果を示す。
PINNsのセットアップ:学習率1×10-3。エポック数50,000。隠れ層の数=2,3,4。幅={20、100}。
㈠ 計算精度・・・PINNsは、およそ100程度。FEMは10-1程度であり、FEMの方が精度が高い。
㈡ 計算時間・・・PINNsは、103秒。一方、FEMは100秒~101秒。FEMが、2~3桁程度速いことになる。
㈢ 評価精度・・・PINNs及びFEMの評価精度は、どちらも計算精度と同程度である(故に、FEMの方が高精度)。
㈣ 評価時間・・・PINNsは、10-1秒~100秒。FEMは、10-1秒に至らない。FEMがおよそ1桁程度速い。
【4】考察
(1) 本論文では、プレーンバニラなPINNsはFEM勝てないと総括している。それは、そうだろう。
ただ局地戦で言うと、プレーンバニラなPINNsでさえ、2次元及び3次元ポアソン方程式では、計算精度・評価精度で勝っている(少なくとも負けていない)。計算時間は負けているが、評価時間では2桁程度速い。PINNsは計算時間で、FEMや差分法と勝負することは想定していないから、評価時間で勝てば十分であろう。
(2) 反応拡散方程式であるアレン・カーン方程式に対して、プレーンバニラなPINNsが役に立たないという結果が得られた。それも、そうなのであろうという感じ。Ⅰ-5 PINNsのベンチマークでは、カオス的挙動を示す偏微分方程式というカテゴリーで、グレイ・スコット方程式(GS方程式)という反応拡散方程式が取り上げられている。GS方程式に対しては、FB-PINNsというバリアントが良い結果を示した。良いといっても10-2程度であるが、本論文におけるFEMの精度は10-1程度であるから、PINNSの方が高精度である。なお、このケースのグランドトルゥースも有限要素法を使った数値解である(ソルバーはCOMSOL)。
アレン・カーン方程式にFB-PINNsが有効かは分からないが、アレン・カーン方程式に相性が良いPINNsを用意すれば良いだけ、という話であろう。
(3) 本論文では、「アレン・カーン方程式は、PINNsと相性が良いと予想した」と書かれているが、「プレーンバニラなPINNsと相性が良い」わけは無いだろう。
(4) なお、本論文では、最適化手法として「まずAdam、その後L-BFGS」が採用されている。既述通り、これはPINNsで普通に使われる(特殊ではないという意味)。L-BFGSに切り替えるタイミングが悪いと性能が落ちることが知られているが、本論文では、その心配はないと思われる。
(5) また、本論文では、初期損失関数の重みを調整することで、たまたま良い結果を得ている。損失関数の重みを調整することで、PINNsの性能を向上させることは、常とう手段である。従って、当然の結果とも言えるだろう。さらに言えば、他の損失関数の重みも適応的に調整させる枠組みを採用すれば、さらに良い結果が得られるであろう。
(6) 半線形シュレーディンガー方程式であっても2次元のケースでは、プレーンバニラなPINNsでさえ、計算精度・評価精度は、FEMに勝っている。その方が、サプライズである。
(7) アレン・カーン方程式は、実務上というか産業応用を考えた場合に、重要な方程式である。ただ、より重要な方程式として、ナヴィエ・ストークス方程式(NS方程式)がある。特に、高レイノルズ数と圧縮性流体を考える必要がある航空宇宙分野でPINNsが使えると、インパクトが大であろう。
(8) 米ブラウン大学の研究者が投稿(@arXiv24年10月22日)したPINNs†1のレビュー論文[*4]には、「(PINNsは大幅な計算速度の向上を達成したものの)PINNsが順問題でFEMに対抗できるかどうかについては、現在議論がある」と書かれている。その一方で、「高次元ではPINNsは、FEMだけでなくあらゆる方法よりも優れている。たとえば、ハミルトン・ヤコビ・ベルマン方程式やフォッカー・プランク方程式などの高次元偏微分方程式に関する最近の研究†2では、PINNsを適切に定式化することで、100,000 次元でも1台のGPUで、わずか1時間で処理できることが実証されている。これは、他の方法では処理できない」とも書かれている。
†1 正確に言うと、[*4]での表記はPINN。本稿での表記に合わせて、ここではPINNsとしている。
†2 24年5月17日@arXivに投稿された論文[*5]。同じくブラウン大学の研究者による論文。
米ブラウン大学の研究者は、「PINNsの進化に着目したレビュー」論文[*4](以下、本論文)を発表した(24年10月22日@arXiv)。構成は、(1)PINNsの一般的なフレームワーク、(2)PINNsの改善を目的とした主要手法の包括的レビュー、(3)アプリケーションのレビュー、(4)PINNsにおける不確実性定量化、(5)PINNs の背後にある理論の発展、(6)ソフトウェア・ライブラリのレビューとなっている。
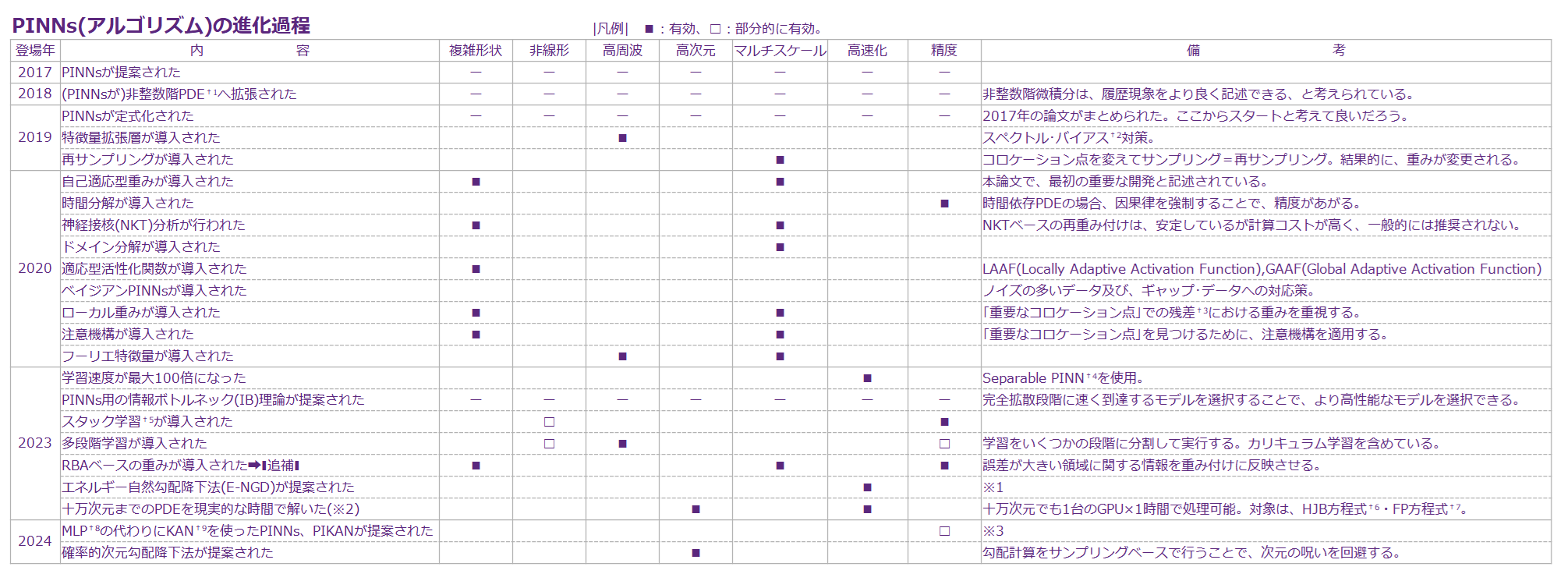
本稿では、本論文の付録にインスパイアされて、PINNsの進化を年ごとにまとめて、注記をつけた。上記の構成で言うと、(2)と(5)が反映されている。
【1】PINNsの進化
下表は[*4]の内容全てを反映していない(取捨選択している)。一方で、他論文等の結果等を反映させている。また、適宜アップデート等を行う。
PINNsにとって非線形性は鬼門である。NNの範囲で、どうこうできる問題ではないかもしれない━為参考━。例えば、高レイノルズ数の流れ(=乱流=非線形性が強い流れ)に対しては、数値計算的なアプローチとして、人工粘性率の導入というアプローチがある。人工粘性率を導入すると、精度(L2相対誤差)が劇的に改善する。人工粘性率に関しては、こちらを参照(改善結果は、その下(3)を参照)。
なお、PINNsの数値解析に関するレビュー論文[*6]†10(24年9月4日公開)は、PINNsが優位性を有するケース(問題)として、以下3つを上げている:
㊀ 高次元問題
㊁ 複雑形状を有する問題
㊂ 逆問題
†1 偏微分方程式(Partial Differential Equation)
†2 深層学習の文脈に置けスペクトル・バイアスとは、「低周波成分の学習が、高周波数の成分より優先される現象」を指す。その結果、高周波成分の学習は、低周波成分の学習よりも(大幅に)遅くなる。
†3 重要な点での残差が、総損失において正当に評価されなければ、重要情報は学習されない。つまり、精度及び収束性低下につながる。
†4 MLP(多層パーセプトロン)に多次元座標を入力する代わりに、複数の部分ネットワークに1次元座標を入力する。解を生成するためのネットワーク伝播の回数が指数関数的に削減される。
†5 ネットワークを順番にスタックすることで、各ステップからの出力が後続ステージの低忠実度入力として機能。予測が段階的に改良される。
†6 ハミルトン・ヤコビ・ベルマン方程式。元々は、最適制御問題において扱われていた。最適ポートフォリオ問題を最適制御問題に置き換えることで、金融(資産運用事業)においても重要な方程式となった。
†7 フォッカー・プランク方程式。確率分布の時間発展を記述する偏微分方程式。「確率の流れ」が保存する(連続の式を満たす)マスター方程式に相当する。
†8 多層パーセプトロン(Multi-Layer Perceptron)
†9 コルモゴロフ・アーノルド・ネットワーク(Kolmogorov Arnold Networks)
†10 Acta Numericaに掲載された論文。数値解析の研究論文を掲載する数学雑誌。英ケンブリッジ大学が発行している。
※1 こちらを参照。
※2 こちらの文献を参照:Junwoo Cho et ai.、Separable Physics-Informed Neural Networks、https://arxiv.org/pdf/2306.15969
※3 こちらを参照。
❚追 補❚ RBAベースの重み:残差ベースの注意(Residual Based Attention)に基づく重み更新スキーム
RBAスキームでは、コロケーション点iにおける、反復回数k+1回目の重みwik+1は、以下のように更新される:
wik+1=γ×wik+η|ri|/max(ri)
ここで、γは減衰率、ηは学習率(オプティマイザーの学習率とは別の値)、riはコロケーション点iにおける残差である。
━為参考━
1⃣ メイン
流体力学について比較的多くの紙幅を割いている[*6]によると、ナヴィエ・ストークス方程式に基づくPDE損失の上限は、定数×f(β)2で表される🐾1。境界損失の上限は、別の定数×f(β)で表される。ここで、βは流れ🐾2に(も)影響される正値パラメータである🐾3。
ここからは、危うい議論であるが、流速が大きくなるとβも大きくなるとする。"ドメイン知識"を動員すると、境界損失は、流速が大きくなっても、それほど大きくはならないと考えられる。しかし、そうであっても、境界損失の2乗に比例するPDE損失は、比較的大きくなりうる。流体力学の場合、流速大=乱流=非線形性が強い、である。つまり、都合の良い解釈を重ねれば、流体力学×非線形性が強い場合、PDE損失の上限が急に上がるので、「収束させるのに苦労するし、汎化誤差も大きくなる」と考えることができるかもしれない。
PINNsが非線形の扱いに苦労しているという先入観を基にした、結論ありきの議論ではあるものの、上記のような構造が存在するならば、高速流れをPINNsで精度良く扱うのが"難しい"のは、数学的に"保証される"ということになる("保証"という言葉は強過ぎるが、数学的に説明ができるという意味)。もちろん、あくまで"難しい(苦労する)"であって、"できないわけではない"。
🐾1 ニューラルネットワークのセットアップとしては、活性化関数がtanhで隠れ層数が2。適応型活性化関数などを使うことで、変わる可能性はあるだろう。
🐾2 具体的に述べると、流速ベクトルと圧力に依存。
🐾3 正確に言うと、PDE損失と境界損失に現れる定数も、流速ベクトルと圧力に依存する。
2⃣ 余談1
PINNsの文脈における、(非圧縮性流体を扱う場合の)流体力学の「支配方程式」は、ナヴィエ・ストークス方程式(NS方程式)🐾4のみならず、「連続の式」🐾5を含めることが理に適っている。便宜上、NS方程式に基づく損失関数をNS損失、連続の式に基づく損失関数をdiv損失🐾6と呼ぶ。div損失は、境界損失と定数倍(物理っぽく表現するとスカラー倍)しか違わない[*6]。
流体力学のPINNsにおける総損失関数を、NS損失+div損失+境界損失と分解した場合&流れが速い場合、NS損失は、他の2つより大きくなる。この差異は、他パラメータの大きさに影響を受けるので、ピタっと決まらないが、粗々で目安を言うと、10倍以上違う。そこで、総損失関数におけるグローバル重みを、「NS損失のグローバル重みのみ0.1(あるいは、0.1より小さい値)にして、他を1.0にする」というのは、合理的と思われる。
🐾4 物理的に述べると、運動量保存則を記述した方程式である。
🐾5 物理的に述べると、質量保存則を記述した方程式である。
🐾6 連続の式が、divu=0と表されることから。uは流速ベクトル、divは勾配演算子∇との内積を意味する。
3⃣ 余談2
[*6]では、PINNsにおけるニューラルネットワークの幅(ノード数)についても、目安を与えている。これも、ピタっとは決まらない。それを承知の上で、粗々の目安で言うと・・・NS損失上限値1%を実現するには、300~400ノード数が必要と考えられる。
【尾注】
*1 所属学科は、応用数学と理論物理学、コンピュータ科学、数学とコンピュータ科学のようである。
*2 Tamara G. Grossmann et al.、CAN PHYSICS-INFORMED NEURAL NETWORKS BEAT THE FINITE ELEMENT METHOD?、https://arxiv.org/pdf/2302.04107.pdf
査読済版は、https://academic.oup.com/imamat/article/89/1/143/7680268
*3 Aditi S. Krishnapriyan et al.、Characterizing possible failure modes in physics-informed neural networks、https://arxiv.org/pdf/2109.01050.pdf
*4 Juan Diego Toscano et al.、From PINNs to PIKANs: Recent Advances in Physics-Informed Machine Learning、https://arxiv.org/pdf/2410.13228
*5 Zheyuan Hu et al.、Tackling the Curse of Dimensionality with Physics-Informed Neural Networks、https://arxiv.org/pdf/2307.12306
*6 Tim De Ryck & Siddhartha Mishra、Numerical analysis of physics-informed neural networks and related models in physics-informed machine learning、https://www.cambridge.org/core/services/aop-cambridge-core/content/view/A059C6E13478F0F7C70EC7C976716F9F/S0962492923000089a.pdf/numerical-analysis-of-physics-informed-neural-networks-and-related-models-in-physics-informed-machine-learning.pdf

