KANのAIは勝つとは限らない
MIT他🐾1の研究者は、「深層学習モデルの基本的な構成要素である、多層パーセプトロン(MLP)の有望な代替を提案」した論文[*1](以下、本論文)を発表した(@arXiv)🐾2。有望な代替とは、コルモゴロフ・アーノルド・ネットワーク(Kolmogorov–Arnold Networks:KAN)である。コルモゴロフ・アーノルド表現定理をベースとしているので、そう名付けられている。なお、KANは「MLPとスプラインの組み合わせ」なので、MLPの代替というのは、表現としてやや不適切と思われる。
巷では、KANを、「パラメータ効率が良く、解釈可能性が高い」ニューラルネットワークと紹介していることが多い。しかし、その表現は、表層的な理解に留まり、本質的な理解を遠ざける可能性があると思われる。そこで、次のような、やや極端な質問を考えてみよう:KANは、MLPを駆逐するほどのインパクトを持っているのか? 答えはNoであろうことは、論理的に推量できる(導出とまではいかない)。KANは、科学(主に、物理学)を相手にする場面で真価を発揮する、特化型のニューラルネットワークと考えられる(☛【3】(2)2⃣参照)。
🐾1 カリフォリニア工科大学、ノースイースタン大学及びThe NSF Institute for Artificial Intelligence and Fundamental Interactions。
🐾2 ver.1は24年4月30日、最新版のver.4は6月16日公開。
ちょい足しは、こちら。
【1】本論文の主張
本論文は、以下を主張する(ここでは頭出しのみ。【4】で詳述):
(0) KANはMLPとは異なり、解釈可能である。
(1) KANはMLPよりも、優れたニューラル・スケーリング則を示す。
(2) KAN は、MLP よりも関数を表現するのに効果的である、KAN は MLP よりも特殊関数を表現するのに効率的で正確である。
(3) KAN は、MLP よりも、偏微分方程式を解くのに適している。
(4) KAN は、MLPとは異なり、「破滅的忘却」🐾3を回避できる(と予想)。
(5) KANは、科学的発見を促進できる。
(6) KAN は、MLP よりも、学習が遅い。
🐾3 破滅的忘却とは、学習モデルが新しいタスクを学習する際、過去に学習したタスクを忘れてしまう現象である。
【2】事前整理
(0) エウレカ前夜:エピソード0[*2]
MIT の大学院生 Ziming Liu(リュー)と彼の指導教官であるMax Tegmark(テグマーク、MITの 物理学者)は、ニューラル ネットワークを科学的アプリケーションでより理解しやすいものにする作業に取り組んでいた。ブラック ボックスの内部を垣間見ることを期待していたが、うまくいかなかった。リューは”絶望のあまり”、コルモゴロフ・アーノルド表現定理について調べてみることにした。「これまであまり注目されてこなかったとしても、試してみて、どのように機能するかを見てみたらどうだろう?」
テグマークは、ポッジョの論文🐾4をよく知っていて、この取り組みはまた行き詰まるだろうと考えていた。しかし、リューはひるむことなく、テグマークもすぐに同意した。リューは約1週間このアイデアに取り組み、その間にいくつかのプロトタイプKANシステムを開発した。これらはすべて2層であり、どれも、彼が考えていた科学関連タスクでうまく機能しなかった。そこでテグマークは、重要な提案をした。2 層以上の KAN を試してみてはどうか。そうすれば、より高度なタスクを処理できるかもしれない。その型破りなアイデアが、ブレークスルーだった。
🐾4 物理学者からマサチューセッツ工科大学の計算神経科学者に転身したトマソ・ポッジオが1989年に共著で発表した論文。この論文は、「KANの核心にある数学的アイデアは、学習のためのネットワークの文脈では無関係」だと明言していた。
(1) コルモゴロフ・アーノルド表現定理
「多変数連続関数は、1変数連続関数の和で表現可能」という驚くべき定理である。1変数連続関数を足し合わせる数は、多変数連続関数の変数の数をnとして、2n+1である🐾5。定理の文言を、深層学習に寄せて言い替えると、「高次元関数の学習は、1次元関数の多項式数の学習に帰着する」となる。
ただし、当該1次元関数は滑らかでなく、フラクタルになることもあるため、実際には学習できない可能性がある。つまり、数学的には驚くべき定理であるものの、深層学習の実用には向かない、と判断されていた。本論文は、創意工夫を凝らして、その障害を乗り越えた、ということになっている。
🐾5 データの構造によっては(特定の条件を満たせば)、2n+1より少なくなりであろう。
(2) Bスプライン関数・曲線
Bスプライン曲線は、CAD(Computer Aided Design)あるいは、コンピューター・グラフィックスの分野において、曲線表現のために広く用いられる曲線である🐾6。流麗な形状を誇るスポーツカーをデザインする場面をイメージすれば良いだろう。数学的には、Bスプライン基底関数と呼ばれる基底関数と「制御点」をかけて、足し合わせたものが、Bスプライン関数である。Bスプライン関数を描画すると、Bスプライン曲線である。
漸化式で構成される🐾7Bスプライン基底関数がn次のときに、n次Bスプライン関数と呼ばれる。また、Bスプライン基底関数の引数は、ノットベクトルと呼ばれる。制御点は、Bスプライン曲線が結んで欲しい点(群)であるが、Bスプライン曲線は、必ずしも制御点を通らない(通らなくて良い、という性質を持つ)🐾8。無理やり制御点を通らなくて良いので、制御点の配置が病的であっても、NTTのマークのような”くるりんぱ”、が生じない。
Bスプライン(スプラインでも同じ)は、低次元関数に対して正確で、ローカルで調整しやすく、さまざまな解像度を切り替えることができる。ただし、Bスプライン(スプラインでも同じ)には、深刻な次元の呪い問題がある。
🐾6 全くの余談であるが、CADでは、実際にはNURBS(非一様有理Bスプライン)が用いられる。NURBSは、制御点に重みを付けたBスプラインである。こうすることで、制御点を増やさずに、表現力を高めることができる。
🐾7 n次Bスプライン基底関数は、2個の「n-1次Bスプライン基底関数」の和で表される、という関係にある。0次Bスプライン基底関数は0もしくは1(ノットベクトルに依存して、異なる)。
🐾8 対して、スプライン関数が作るスプライン曲線は、制御点を必ず通る。例えば、金融におけるイールド・カーブ(本来は、ゼロ・イールド・カーブが好ましい)を構成する場合などは、スプライン曲線でなければ都合が悪い。なお、3次スプライン曲線は、曲がりによる歪エネルギーが最小になることが証明されている。つまり、物理的に最も自然な曲線であることが、数学的に保証されている(ので、通常、スプライン曲線を使う場合は、3次スプライン曲線を使う)。
(3) 誤差逆伝播法
深層学習の歴史を振り返ってみると、単層パーセプトロンは排他的論理和(XOR)を実行できなかった。これは、多層パーセプトロン(MLP)にすることで、解決できた。ただ、MLPを学習する方法(パラメータを更新する手続き)が難しかった。それは、誤差逆伝播法によって解決された。誤差逆伝播法は、2024年ノーベル物理学賞を受賞した、ジェフリー・ヒントン(トロント大学名誉教授)が考案・開発した。誤差逆伝播法は、損失関数(今の場合、コスト関数でも同じ)の勾配を計算する必要がある。つまり、損失関数は微分可能である必要がある。
コルモゴロフ・アーノルドの表現定理に従ってKANを構成すると、1次元関数が滑らかな関数でない可能性があるため、損失関数の微分可能性が保証されない。このため、誤差逆伝播法を使った学習が行えない可能性がある。この懸念は、部分的に(?)解消されたであろうと、されている。これは、以下のような意味である(これは、本論文に記述されているわけではない):確かに、滑らかでない関数をBスプラインで近似することによって、滑らかでなかった関数を"可微分にすることができる"ため、誤差逆伝播法が使えないという事態は避けられる。しかし、"無理やり強引に、可微分にしたことの代償"として、近似誤差がどれだけ悪化するか?という数学的な議論は尽くされていない。従って、(KANは、計算コストが増加するという代償を含め)MLPをKANに置き換える意味が、"無理やり強引に、可微分にした"ケースにあるか?は、未解決である(と思われる)。☛【3】(1)1⃣及び(2)2⃣も、併せて参照。
【3】KANのモデル・アーキテクチャ
(0) 概要
0⃣ 一言で言い表すと・・・
KAN はスプラインと MLP の組み合わせに過ぎない。組み合わせることで、それぞれの長所を活用し、それぞれの弱点を回避している。
1⃣ KANの特徴を、観念的に表現すると・・・
関数を正確に学習するには、モデルは外部自由度を学習するだけでなく、内部自由度(単変量関数) も適切に近似する必要がある。KAN は、外側に MLP、内側にスプラインを持つため、関数を正確に学習できるモデルと考えられる。さらに、KANは(MLP との外部類似性により)特徴量を学習できるだけでなく 、(スプラインとの内部類似性により)学習した特徴量を非常に正確に最適化することもできる。
2⃣ MLPと対比した、ステレオタイプなKANの概要説明
擦られ過ぎているステレオタイプな説明をすると、以下のようになる:
MLP→学習可能なパラメータを持つ関数による線形変換+パラメータを固定された非線形変換
KAN→ 学習可能なパラメータを持つ関数による非線形変換
なお、本論文において、「ニューラルネットワークにおける、学習可能な活性化関数の考え方は、新しいものではない」ことが、示されている。
3⃣ 同じく、ステレオタイプなアーキテクチャの概要説明
MLPと同様に、KAN は全結合構造を持っている。計算グラフでアーキテクチャを説明すると、MLPは固定の活性化関数をノードに配置している。対して、KAN は、学習可能な活性化関数をエッジに配置している。その結果、KAN には線形重み行列が全くない。代わりに、各重みパラメータは、スプラインとしてパラメータ化された学習可能な 1次元関数に置き換えられる。KAN のノードは、非線形性を適用せずに、入力信号を単純に合計する。
4⃣ 近似精度
KANは、以下の精度で、多変量関数を近似できる。
||多変量関数-KAN||≦定数×G-(k+1)+m
ここで、ノルムはCmノルム、Gはグリッド数🐾9、kはBスプライン基底関数の次数、mは0≦m≦kを満たす任意の整数である。Cmノルムは、m=0でL∞ノルムになる(ので、L∞ノルムという認識で良いだろう)。定数は、次元(多変量関数の変数の数)に依存する。この、定数の次元への依存性に関する議論は、本論文では、「今後の作業として残しておく」とされている。
例えば、k=3(通常の値)、G=100とすると、定数×10-8で抑えられることになる。Cが病的に大きな数でない限り、近似誤差は、十分な精度で抑えられると考えられる。
🐾9 ノット・ベクトルの数、ノット数。
5⃣ 為念:KANを表す記号
KANを表す記号[n, 2n + 1, 1]は、入力ノードの数nに対して、中間層のノード数が2n+1、出力ノードの数が1であることを示している。また、この[n, 2n + 1, 1]は、以下で言及される、2層2n+1幅のネットワークのことである。
(1) 本論文の創意工夫
0⃣ 創意工夫の概要
元のコルモゴロフ・アーノルド表現を、「任意の幅と深さ」に一般化した。
1⃣ 創意工夫の詳細
コルモゴロフ・アーノルド表現定理(KAT)の本質を、簡略的な「数式もどき」で表現すると、
n変量関数=∑q関数(∑別の関数(単変数)) (q=1~2n+1)
となる。ここで強調したかったことは、㊀関数・別の関数という『2層構造』の存在、㊁足し合わせの数が2n+1、ということである。この「数式もどき」をニューラルネットワーク的に表現すると、深さが2(出力層を含めると3)、幅が2n+1のネットワーク、ということになる。そして、本論文は、以下のように批判する:KATを深層学習に応用する研究は、これまで、ほとんど(オリジナルの)2層「2n + 1」幅表現に固執しており、ネットワークを学習するための、より現代的な手法(誤差逆伝播法など)を活用する機会がなかった。本論文は、2層「2n + 1」幅という縛りを破棄することで、ブレークスルーを果たした。
障害は、2層という浅いネットワークだと、「滑らかとは限らない」1次元関数(KATで言えば、単変量関数)を、Bスプライン基底関数で適切に近似することはできない、ことであった。本論文では、解決策はネットワークを深くすることだと、としている。ただし、これは数学的に証明されていない。深さ2がダメ🐾10なので、より深くしてみよう、ということ(仮説)に過ぎない。「深くすれば、滑らかに表現できる」ことは証明されていないし、「どれだけ深くすれば良いか」も分かっていない。本論文では、様々な数値実験を行って、先の仮説に対して、検証を行っている(に過ぎない)。この問題については、☛(2)2⃣。
「深くすれば、滑らかに表現できるか?」は、ひとまず置いて、「深くすれば、滑らかに表現できる」とする。その場合でも、「深くするとは、なんぞや?」を考える必要がある。思索の結果、KANのネットワークを深くするという意味は、MLPと同じで、単純にKAN層を積み重ねるだけであった。
🐾10 深さ2のコルモゴロフ・アーノルド表現では、滑らかに表現できない関数が存在することが示されているので、深さ2でダメなことは、容易に証明される。
2⃣ 実装に関する追加情報
㈠ 活性化関数
活性化関数=係数×(Swish活性化関数+3次Bスプライン関数)
活性化関数=係数1×Swish活性化関数+係数2×3次Bスプライン関数
ver1及びver2では上の式。ver3から(最新版のver4でも)下の式に変更されている。
㈡ 初期化
各活性化関数は、Bスプライン関数 ≈ 0 になるように初期化される。係数は、MLP の線形層を初期化するために使用されている Xavier 初期化に従って初期化される。
3⃣ パラメータ数
KANには、O(N2L(G + k))~O(N2LG) 個のパラメーターがある。NはKANの幅、LはKANの深さ。Gはグリッド数(🐾9参照)、kはBスプライン基底関数の次数。一方、MLPには、O(N2L)個のパラメータがある。
本論文によると、「KANのNは、MLPのNよりも遥かに小さい」。このため、パラメータ数は、KANの方が少ない、とする(☛【4】(3)参照)。
(2) KANに残された障害
1⃣ 小さな障害ー実行速度が遅い
KAN の(表面上の)最大のボトルネックは、学習が遅いことである。KAN は、同じ数のパラメータがある場合、通常 MLP より 10 倍遅い。ただ本論文には、次のような告白がある:『正直に言うと、KAN の効率を最適化するために一生懸命努力したわけではないので、KAN の学習が遅いことは、根本的な制限ではなく、将来改善されるべきエンジニアリングの問題であると考えている』。
さらに本論文では、スピードアップの施策提案もされている:『KAN の実行速度が遅い主な理由の 1 つは、異なる活性化関数がバッチ計算を活用できないことである。実際には、活性化関数を複数のグループにグループ化することで、活性化関数がすべて同じ(MLP)とすべて異なる(KAN)の間を補間できる(ので、スピードアップが可能となる)』。
2⃣ 大きな障害
実行速度が遅い、はカワイイ問題で、大問題は、「層を深くすれば、滑らかに表現できる」とは限らない、ということである。しかし、この問題に関して、本論文は楽観的である:科学において遭遇するほとんどの関数は滑らかである。従って、少なくとも科学を対象とする限り、KANは機能するというヨミがある。
そのため本論文は、KANに、特殊関数を表現させたり、偏微分方程式を解かせたり、ファインマン・データセットを使ったり、結び目理論やアンダーソン局在に応用したりしているわけである。マーケティング分野🐾11の深層学習アプリケーションや、自然言語処理(NLP)に使えるかは、疑問である(もちろん、使えるケースは、いくつかあるだろうが、その範囲がどこまで広いかは疑問)。金融は、いけるかもしれない。
本論文の著者は、KANを「AI+科学の言語モデル」とすることを目指している。言葉を替えると、KANによって基礎科学(主に、物理学)の発見を促進することを目的としている。それは、本論文の著者他によって書かれた、後続論文である”KAN 2.0: Kolmogorov-Arnold Networks Meet Science” (24年8月19日@arXiv)[*3]が、「KANと科学をシームレスに相乗させるフレームワークを提案」し、そのフレームワークを用いて「保存量、ラグランジアン、対称性、構成法則など、様々なタイプの物理法則を発見するKANの能力を実証」していることからも伺える。
ちなみに、以下の発言がある:「KAN は解釈しやすく、データから科学的ルールを抽出できる科学アプリケーションに特に役立つ可能性があります」(ジョンズ ホプキンス大学(コンピューター科学)のアラン・ユイル教授)[*2] 。
🐾11 1 ヶ月の購買状況を基に、翌月の購買金額を予測するというタスクにKANを適用した実験を行った結果が[*4]に示されている。KANと参照モデルを比較している。KANは20種類(深さ、幅に加えて、オプティマイザー、スケジューラーでバリアント作成)。参照モデルは、MLP(活性化関数がtanhとReLU)、LightGBM、XGBoost、SVM、k-近傍法。結果は、KAN優勢(汎化誤差小さい)であるが、あまり意味はないだろう。
👔ちょい足し情報👔
シンガポール国立大学の研究者がarXivにて(ver1が7月23日、ver2が8月17日に)公開した論文[*5]は、「シンボリック回帰式(表現)、機械学習(タスク)、コンピューター・ビジョン(画像認識)、自然言語処理(NLP)、音声処理」において、MLPとKANの”公正な”比較を行った。その結果は、シンボリック回帰式(表現)以外は、MLPがKANに勝った。[*5]は1ページ目に、結果を視覚的に表示しているので、一読をお薦めする。画像認識、音声処理はMLP圧勝。機械学習(タスク)とNLPは辛勝。
【4】本論文主張の詳細と、その根拠
本論文のキモは、ここに集約される。
(0) KANはMLPとは異なり、解釈可能である。
0⃣ 説明可能性
説明可能性と解釈可能性を区別すると、理解が進むかもしれない。ちなみにAIの説明可能性は、通常、2 つの手法を使用してアプローチされる: モデル固有の方法と、モデルに依存しない方法である。DeepLIFT、Grad-CAM、Integrated Gradientsなどの「モデル固有の方法」は、特定の種類のモデルの動作を説明するように設計されている。一方、LIME や SHAPなどの「モデルに依存しない方法」は、モデルの内部動作に依存せずに、あらゆる機械学習モデルの予測を説明することを目的としている。 これらの方法は、さまざまな種類のモデルに適用でき、より汎用性の高い解釈ツールを提供する。
どちらの手法も「重要な特徴量(説明変数)を抽出することで、AIを説明可能としている」。つまり、説明可能性=どの入力が、出力を支配しているか、を説明できるか?である。
1⃣ 解釈可能性
一方、解釈可能性=系全体を解釈(する手段を提供)できるか?である。KANは、「学習対象の物理系を記述する支配方程式を(適確に)書き下すことができるため、解釈可能性が高い」と主張している。学習モデルによって支配方程式を(自動的に)書き下す手法として、シンボリック回帰(SR)が知られている。本論文は、SRについて、次のように述べている(要約すると、KANはSRより優れている):「SRは、一般に脆弱でデバッグが困難である。解釈可能な中間結果を出力せずに、最終的に成功または失敗を返す。対照的に、KAN は関数空間で連続探索(勾配降下法を使用)を行うため、結果はより連続的であり、従って、より堅牢である」、「ターゲット関数がシンボリックでない場合、SRは失敗するが、KANは意味のある何かを提供できる。たとえば、特別な関数(ベッセル関数など)は、事前に提供されない限りSRが学習することは不可能であるが、KAN はスプラインを使用して数値的に近似できる」。
2⃣ とは言え・・・
説明可能性に寄せて、KANの解釈可能性が高い理由を、表現する事も可能である。曰く:
㈠ 各変数が目的変数に与える影響について、(アドオン・ツールを使うことなく)可視化することが可能という意味において、従来手法より高い解釈可能性を持っている。
㈡ ネットワーク全体は深層構造であるものの、各層レベルでは、常に単変数の計算となる。このため、解釈性が高まる。
㈢ KANでは活性化関数による非線形変換の後に総和を取る。このため、ノード間における変数の関係性に対する解釈性が高いとされる。
3⃣ 改めて、KANが意図する解釈可能性が、一般的な意味とは異なる理由
それは、KANが、科学を主な対象にしているからである。
(1) KANはMLPよりも、優れたニューラル・スケーリング則を示す。
ニューラル・スケーリング則は、モデルのパラメーター数が増えるとテスト損失(汎化誤差)が減少する現象である。パラメータ数以外の、計算量やデータセットのサイズが増えてテスト損失が減少する現象も、ニューラル・スケーリング則と呼ばれる。「数式もどき」で表すと、テスト損失∝パラメーター数-スケーリング指数である。
本論文によると、MLPは、活性化関数がk次の区分多項式である場合、スケーリング係数=(k+1)/2である。対して、KANは、Bスプライン基底関数の次数をkとした場合、スケーリング係数=k+1である。従って、結論に達する。
(2) KAN は、MLP よりも関数を表現するのに効果的である。KAN は MLP よりも特殊関数を表現するのに効率的で正確である。
1⃣ 関数
『滑らかなコルモゴロフ・アーノルド表現を持つことがわかっている』5 つの関数を対象に、KANとMLPを、合計 1800 ステップ・オプティマイザーLBFGSで学習した。KANは、200ステップ毎にノット・ベクトル(グリッド)の数を増やした❚補足1❚:G={3、5、10、20、50、100、200、500、1000}。
ニューラル・スケーリング則(つまり、パラメータ数に対するテスト損失の挙動)で、KANとMLPを比較した。テスト損失は、RMSEで測る。KANは、高次元(100次元)の1例を除いて、理論的なスケーリング則に近い挙動を示した。一方、MLPは、理論的なスケーリング則に追従することが困難であった🐾12。
🐾12 MLPは例外的に、高次元(100次元)の例だけ、理論的なスケーリング則に近い挙動を示すが、理論的なスケーリング則自体が、N-0.04とほとんどスケーリングを示さない。また、理論値含めて、テスト損失が大きい(10-1程度)ので、あまり意味はない。
❚補足1❚ グリッドの数を増して、精度を上げる
KANは、最初にパラメータの少ない KAN を学習し、次にグリッド数を増やす(粒度を細かくする)だけで、より大きなモデルを最初から再学習することなく、より多くのパラメータを持つ KAN に拡張することができる。そして、KANの優れたニューラル・スケーリング則により、パラメータ数の増加に伴って、テスト損失が減少する(という仕組みである)。
2⃣ 特殊関数
数学と物理学で一般的な 15 個の特殊関数🐾13を対象とした。MLPは、固定幅 5 または 100、深さ {2、3、4、5、6}。KAN は、「枝刈り❚補足2❚有り」と「枝刈り無し」の両方で実行する。枝刈り有りは、スパース化❚補足3❚と枝刈りを使う。枝刈り無しは、幅を 5 に設定し、深さを {2、3、4、5、6}とする。また、KAN は G = 3 に初期化され、オプティマイザーとしてLBFGS を使って学習され、200 ステップごとにグリッド数が増える。すなわち、G = {3、5、10、20、50、100、200}。
結果は、KANはスケーリング則が観察できるが、MLPは観察できない。また、(RMSEで測る)テスト損失の最小値は、MLPの場合、概ね 10ー3程度。KANの場合、概ね 10-5、もしくはそれを下回る。結論として、KANのほうが、優れていると言えるであろう。ただ、パラメータ数が102程度までなら、テスト損失は、MLPもKANも、それほど変わらない。
🐾13 ヤコビの楕円関数、第一種不完全楕円積分、第二種不完全楕円積分、ベッセル関数(1次、2次)、修正ベッセル関数(1次、2次)、ルジャンドル陪関数(3種類)、球面調和関数(5種類)。
❚補足2❚ 枝刈り(pruning)
ℓ層のノードiに対して、入力スコアと出力スコアを計算し、その両方が、しきい値10−2より大きい場合、ノードを重要と見なす。重要でないノードは全て削除される(つまり、枝刈りされる)。スコアは、活性化関数のL1ノルムで計算される。活性化関数のL1ノルムは、(本論文において)入力に対する平均振幅で定義される。入力スコアは、ℓ層のノードiに出力されるℓ-1層の全ノードに渡るL1ノルムの最大値。出力スコアは、ℓ層のノードiから出力されるℓ+1層の全ノードに渡る最大値。
❚補足3❚ スパース化
本論文曰く、「MLP では、スパース(疎)な解を優先するために、線形重みの L1 正則化が使用される(※L1正則化では、スパース性の高い解が得られる)」。この”スパース化”を、KANでも実行する。ただし、KAN に線形重みはない。線形重みは、学習可能な活性化関数に置き換えられるため、活性化関数の L1 ノルムを準備する必要がある。その上で、KANはL1正則化だけでは不十分なため、エントロピー正則化を併用する。つまり、KANのコスト関数=損失関数+係数×(L1正則項+エントロピー正則項)、となる。係数は、10−2または 10−3を使用する。
3⃣ ファインマン・データセット
ファインマン・データセットとは、ファインマンの教科書に掲載されている物理方程式に現れる関数を指しているようである。例えば、exp(-θ2/(2σ2))/√2πσ2のようなガウス型の関数が含まれている。本論文では、27個の関数に対して、3種類のKANとMLPを学習させた。KAN は G = 3 に初期化され、LBFGS で学習され、200 ステップごとにグリッド数が増加する:G = {3、5、10、20、50、100、200}。また3種類のKANとは、㊀人間が構築した KAN、㊁枝刈り無しのKAN。幅5、深さ{2,3,4,5,6}、㊂枝刈り有りのKAN。スパース化を併用。MLPは、幅20、深さ{2, 3, 4, 5, 6}、活性化関数を{tanh、ReLU、SiLU} から選択。
最小のテスト損失を達成した個数をあげると、㊀3個、㊁10個、㊂5個であり、MLPは9個であった。本論文では、ファインマン・ データセットは、KANが威力を発揮するには単純すぎる、と推測している。
(3) KAN は、MLP よりも、偏微分方程式(PDE)を解くのに適している。
PDEを解くというタスクに優劣を付ける枠組みとして、PINNs(Physics-Informedニューラルネットワーク)を利用している。具体的に言うと、MLPベースのPINNsとKANベースのPINNsとを比較し、どちらの誤差(=グランド・トルゥースとの差)が小さいか?で優劣を付ける。
本論文では、2次元ポアソン方程式を対象としている。境界条件はディリクレ条件。損失関数は、係数×PDE損失+境界損失(係数は、0.01と設定)。誤差はL2ノルムとH1ノルム🐾14で計測した。その結果は、2層10幅のKANは、4層100幅のMLPよりも、①100倍正確で、②100倍パラメータ効率が高い。①は、L2ノルムで計測した誤差が、KANでは10−7であるのに対して、MLPでは10−5でサチュるという意味である。H1ノルムでも結論は同じ。100倍程度の違いがでる。②は、次の意味である:L2ノルムで計測してもH1ノルムで計測しても、MLPはパラメータ数104で、誤差が下げ止まる。そのレベルを、KANは、パラメータ数102程度で達成する。
本論文では、「KANはPDEのモデル削減のための優れたニューラルネットワーク表現として機能する可能性があると推測している」と結論付けている。
🐾14 H1ノルム(エネルギーノルム)||・||H1は、以下で良いだろうか?[*6]
||f||H1=√(||f||2+||∇f||2)
ここで、||・||2はL2ノルム。
👔ちょい足し情報👔
1⃣ 清華大学他の研究者が、arXivにて6月(ver1、最新のver2は8月4日)に公開した論文[*7]:Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov Arnold Networksでは、「マルチスケール問題、特異点問題、応力集中問題、非線形超弾性問題、不均質問題、複雑形状問題」などに対して、MLPベースのPINNsとKANベースのPINNsを比較した。その結果、複雑形状問題を除き、精度と収束速度に関してMLPを大幅に上回ることが実証された。
2⃣ 米ブラウン大学と米パシフィック・ノースウェスト国立研究所の研究者も、PINNsとPIKAN(KANベースのPINNs)を、科学(物理学)分野の多様なケースに対して、出来る限り公正に比較した論文[*13]を発表した(24年6月5日@arXiv)。その結果は、8戦中「PINNs・DeepONet4勝、PIKAN・DeepOKAN3勝、1引き分け」である。詳しくは、こちらを参照。
(4) KAN は、MLPとは異なり、「破滅的忘却」を回避できる(と予想)。
まず、本論文では、破滅的忘却の原因を、「MLPを含むほとんどのニューラルネットワークには、局所性の概念がない」からだ、とする(あくまで推測)。ここで言う局所性とは、人間の脳のように、学習の影響が局所的な範囲に限定されるという意味である。その上で、本論文は、「KAN には局所的な可塑性があり、スプラインの局所性を活用することで破滅的な忘却を回避できる」と主張する(”局所性”推測に基づく主張)。
具体的に言うと、スプライン基底は局所的であるため、学習は近くのスプライン係数のいくつかにのみ影響し、遠くの係数はそのまま残る、とする。対照的に、MLP は通常、ReLU/tanh/SiLU などの、非局所的な活性化関数を使用するため、局所的な変更は遠く離れた領域に伝播するだろう、と推測している。
👔ちょい足し情報👔
シンガポール国立大学の研究者がarXivにて(ver1が7月23日、ver2が8月17日に)公開した論文[*5]によれば、「KANの破滅的忘却問題は、KANの論文(=本稿でいうところの本論文)で報告された結果とは異なり、標準的なクラス増加型継続学習設定においてMLPよりも深刻であることが分かった」。(※下線は、[*5]にはない。便宜上、本稿で加えた)
(5) KANは、科学的発見を促進できる。
0⃣ 概要
「KANは、科学的発見を促進できる」の意味は、「ヒトとKANがコミュニケーションをとり、KANがヒトに示唆を与える形で、物理系の理解が促進される」という意味である。何度も述べているようにKANは、科学をメインターゲットにしている。KANは元々、「ニューラル ネットワークを科学的アプリケーションでより理解しやすいものにする」という目的から生まれている。そして、データから科学的ルールを抽出して、ヒトによる科学的発見を促進することを、(最終的な)目的としている。本論文では、露払いとして、結び目理論とアンダーソン局在を、扱っている。
1⃣ 結び目理論
㈠ 前説
グーグル(ディープマインド)が、2021年の論文[*8]で扱ったので、結び目(正確には、3次元球面の双曲結び目🐾15)を取り上げたのであろう。分類タスクに殉じれば、結び目理論は、柔らかい幾何学とも呼ばれる位相幾何学(トポロジー)に分類できる。トポロジーは、理論物理学の様々な分野に応用されている(もちろん、数学の様々な分野でも使われている)。結び目理論も、御多分に漏れず、様々に応用されている。例えば、環状のDNAは、結び目や絡み目を構成する。暗号分野(秘密計算)の分野でも結び目は使われている。結び目・絡み目→組紐(braid)群は、量子誤り訂正にも応用されている。
🐾15 結び目の補空間が双曲多様体の構造をもつとき、その結び目を双曲結び目と呼ぶ(らしい)。また、「感覚的には。ほとんどの結び目は双曲結び目である](らしい)[*9]。
㈡ 検証課題のセットアップ
具体的には、結び目不変量の一つである、符号数❚補足4❚を予測する問題(以下では、単に”同問題”と呼称する)で、KANが解釈可能な良好な結果を達成できるかどうかを検証した。同問題は、[*8]で扱われている。ザックリ言えば、MLPを使ったグーグルの結果を、「KANは遥かに小規模なネットワークと、遥かに高度な自動化で再発見した」。さらに、新しい結果を提示した。
❚補足4❚ 符号数
低次元位相幾何学には、3次元多様体上の双曲構造から導かれる不変量と、4次元多様体への接続を持つ不変量の2つの非常に異なるタイプの不変量がある。後者のタイプのうち、最も基本的な不変量の1つは結び目の符号数である[*10]。3次元球面の双曲結び目のカスプ幾何は、結び目の符号数に関する情報を符号化する。
結び目の符号数を文章だけで説明するのは、やや難しい。流れだけ述べると、1次元の絡み目=結び目L、に対する対称化行列Mを作り、Mを適当に対角化する。この対角化行列における、「正の対角成分」と「負の対角成分」の差が、符号数である。例えば、[*11]を参照。
㈢ 具体的な比較結果
[17, 1, 14] KANは、テスト・データセットに対して81.6% の精度(accuracy)を達成できた。一方、グーグルの4 層300 幅MLP は 精度78%であった。[17, 1, 14] KAN(G = 3、k = 3)には、≈ 200 個のパラメーターがあるが、MLP には ≈ 3 × 105 個のパラメーターがある。KAN が MLP よりも正確で、同時にパラメーター効率がはるかに高い。
㈣ 新しい結果
グーグルの結果(MLPの結果)は、メリディオナル❚補足5❚μの虚部(μi)が符号数の予測において重要な役割を果たしている、ことを示していた。一方、本論文の結果は、μの実部(μr)が符号数の予測において重要な役割を果たしている、ことを示していた。
KANは、符号数の表現式を(シンボリック回帰のように)自動出力して🐾16、本論文の結果である「μの実部が符号数の予測において重要な役割を果たしている」ことを確認した。正確には、μiを含まない表現式でも、そこそこの精度(77.8%)であることを確認した。[*8]で、科学者が発見した(μi、μr、λ🐾17を含む)符号数の表現式の精度は、83.1%であった。
❚補足5❚ 子午線(経線)を意味するmeridionalである(本論文ではmeridional distance、[*8]ではmeridional translationと表記されている)。おそらく、適当な日本語訳はない。双曲結び目の最も重要な幾何学的特徴の1つはカスプであり、このカスプの境界は、(ユークリッド)トーラスである。トーラスの子午線≃カスプの幾何学的特徴であり、「カスプ幾何は、結び目の符号数に関する情報を符号化している(❚補足4❚参照)」ので、子午線が符号数の予測に関わってくる。
🐾16 具体的には、[c1-c2(1-c3μr)2]/[c4(c5-μr)2+c6(1-c7λ)2+c8]。ここで、ciは定数。λは、下記🐾17を参照。
🐾17 μは経線(子午線)であり、λは緯線(ロンギチュード)である。
2⃣ アンダーソン局在
㈠ 前説
アンダーソン🐾18局在は、量子システム内の無秩序が電子波動関数の局在化につながり、すべての輸送が停止する基本的な現象である。1 次元と 2 次元では、スケーリングの議論により、すべての電子固有状態は、無限小量のランダム無秩序に対して指数関数的に局在される。対照的に、3 次元では、臨界エネルギーが、拡張状態と局在状態を分離する相境界を形成する。これは移動度端と呼ばれる。移動度端を理解することは、固体における金属絶縁体転移や、フォトニックデバイスにおける光の局在化効果などのさまざまな基本現象を説明するために不可欠である。具体的には、移動度端を示す微視的モデルを開発する必要がある。
🐾18 フィリップ・ウォーレン・アンダーソンが、その可能性を指摘した(1958年)。アンダーソンは1977年ノーベル物理学賞を受賞している。
㈡ 問題のセットアップ
移動度端を示す微視的モデルの開発は、ランダム無秩序の代わりに準周期性を導入することで、局在相と拡張相を分離する移動度端が得られる低次元でより実用的になることが多い。本論文では、準周期強束縛模型から生成された数値データに KAN を適用して、その移動度端を抽出する。移動度端の学習は、秩序パラメータの学習にかかっている。
検討するモデル・クラスは、モザイク・モデル(MM)、一般化オーブリー・アンドレ・モデル(GAAM)、修正オーブリー・アンドレ・モデル (MAAM)の 3 つである。全てにおいて、「ヒトとKANがコミュニケーションをとり、KANがヒトに示唆を与える形で、物理系の理解が促進される」という絵が描かれている。しかし、中身(展開される物語の台本)は全くピンとこないので、省略する。
㈢ 結果
モザイク・モデルでは、KANは秩序パラメータの表現式を正確に抽出できる。抽出できるの意味は、理論式を精度よく近似する多項式を(シンボリック回帰のように)出力する、という意味である。GAAMでは、(グランドトルゥースに対して)99.0%の精度(理論式に対してなら、99.8%の精度)で抽出できる。GAMMの理論式はαE+2(λ-1)。KANの出力は、21.06αE+45.13λ-54.45、であった。
MAAMの場合は、(グランドトルゥースに対して)97.1%の精度(理論式に対してなら、99.5%の精度)であった(ヒトの手を加えると、97.1%が97.7%に上がった)。
3⃣ そしてKAN2.0[*3]
今のところ、とりあえず省略。
👔ちょい足し情報👔
量子アプリケーションにKANを適用した論文KANQAS: Kolmogorov-Arnold Network for Quantum Architecture Searchが、arXivにて公開された(24年7月22日)[*12]。為念:KANに量子化(機械学習の文脈における量子化ではなく、量子力学の意味での量子化)するという方向の論文ではない。具体的には、量子回路設計と量子化学タスクにおける、量子アーキテクチャ探索(QAS)アルゴリズムをMLPベースからKANベースに変更して、その効果を分析した。つまり量子アプリケーションで使われる機械学習アルゴリズムをMLPベースからKANベースに替えた、という話である。
量子回路設計の結果は、(ノイズのないシナリオにおいて)「多量子ビットの最大もつれ状態を生成するための最適な量子回路構成の成功確率と数は、MLPベースのアプローチよりも、2倍から5倍高いことが示された」とする。量子化学タスクでは、「2量子ビットゲートが少なく、深度が浅いアンザッツを設計することができ、基底状態を求める効率が向上した」、とする。
(6) KAN は、MLP よりも、学習が遅い。
【3】(2)1⃣を参照。
【5】展望とか感想とか
(1) 本論文は、「PINNs、フーリエ・ニューラル演算子、PINO(Physics-Informed ニューラル演算子)、DeepONetのすべてで、MLP を KAN に置き換える可能性がある」という期待を述べているが、PINNsに関しては”少なくとも[*7]では”良い結果が出ている。
また、「KAN は AI と人間のコミュニケーションを可能にする、最初の言語の 1 つになる」という野望も、実現の可能性は高いかもしれない。
(2) 一方、「トランスフォーマーにおいて、MLPをKAN に置き換える"カンスフォーマー"を提案することもできる」という野望も描いているが、こちらはどうだろうか?
(1) 課題と制限
① KANは、学習が遅く、多くの計算リソースを必要とする傾向がある。その傾向は、複雑で高次元のタスクにおいて顕著である。
② KANは学習データ内のノイズに特に敏感である。ノイズ低減には、カーネル・フィルタリングやオーバーサンプリングといった高コスト手法が必要であり、計算効率を悪化させる。
③ スケーラビリティが制限される❚補足❚。
④ KANは、その複雑で多層的な構成が、解釈可能性を低下させている。高次元データや非線形データを扱う場合は、特に、SHAP†1やLIME†2を援用することが望ましい。
†1 為念:SHApley Additive exPlanations
†2 為念:Local Interpretable Model-Agnostic Explains
⑤ PIKAN(KAN)は、偏微分方程式(PDE)を解く際の精度と収束速度で、PINNs(MLP)を上回る(ケースが存在する)が、複雑な境界条件では苦戦する可能性がある。
❚補足❚
ここで言うスケーラビリティは、いわゆる「次元の呪い」から逃れ(られ)る能力を意味している。KANは、教科書的には、MLPに比べてスケーラビリティに優れているとされる。ここでの主張は、「実際は、関数近似に使用されるスプライン補間の複雑さから、スケーラビリティが制限される」という主張である。ただし、関数近似に、スプライン関数を使わないKANのバリアントは数多く存在する。それらを使った場合のスケーラビリティ制限に関する議論は[*22]において、行われていない。
(2) 最適化に関する課題と解決策
0⃣ 問題の整理
KANにおける最適化は、高次元関数近似の複雑さゆえに不可欠である。KANの強みは、多変数関数を単変数スプライン関数に分解する能力にある†3が、このプロセスの有効性は、これらのスプラインの最適化に依存する。最適化では、スプライン基底関数の制御点とノット・ベクトルを調整することで、予測出力と実際の出力間の誤差を最小化する。しかし、これらの近似の高次元性と複雑さは、㈠、㈡のような課題をもたらす。
†3 つまり、オリジナルのKANが想定されている。
㈠ 非線形パラメータ空間
MLPと異なり、KANではスプライン・パラメータの調整が必要となるため、最適化地形は非線形になり、最適化が困難になる。
㈡ 計算オーバーヘッド
学習可能なスプラインの柔軟性は、学習中の計算負荷を増加させ、最適化の速度とリソース消費を増加させる。
1⃣ KAN固有ではない一般的な解決策
KANの最適化における課題を踏まえ、収束性と性能を向上させるためにいくつかの手法が採用されてきた。
① 確率的勾配降下法
モメンタムを用いた確率的勾配降下法(SGD)などの勾配降下法の派生法は、モメンタムを用いて鞍点を回避することで、非線形最適化の難しさを軽減する。
② Adamオプティマイザ
Adamは、モメンタムと適応学習率を組み合わせたオプティマイザである。各パラメータの学習率を個別に調整できるAdamは、KANの複雑なスプライン関数の最適化に有益である。
③ 過学習の防止
KANでは、スプラインの柔軟な性質により、過学習は一般的な問題となる。高次元空間における過学習を防ぐためKANでは、L2正則化とドロップアウトが一般的に用いられる。これらの手法は、スプラインの柔軟性を制限し、学習データ内のノイズへの適合を防ぐのに役立つ。なお、スパース正則化も過学習を防ぐために、有用とされている。
④ バッチ正則化及び勾配クリッピング
学習を安定化し、収束を高速化するために、KAN層ではバッチ正則化がよく適用される。この手法は、深く複雑なネットワークでよく見られる勾配消失や勾配爆発の解決に有用である。
勾配クリッピングは、学習中の勾配のサイズを制限することで、逆伝播中に勾配が爆発する問題を防止する。これにより、学習プロセスが安定し、モデルが過学習しやすい鋭い解に収束するのを防ぐ。
⑤ 初期化
スプライン・パラメータの初期化が不十分だと、収束が最適でなくなったり、最適化が局所最小値で停滞したりする可能性がある。He初期化やXavier初期化などは、最適化のためのより良い出発点を提供することで、これらの問題を軽減できることが研究で示されている。
⑥ 収束性の向上
KANは学習可能なパラメータの数が多いため、特に高次元データを扱う場合、最適化の収束が遅くなる。さらに、スプライン基底関数の形状と位置の両方を最適化する必要があるため、MLPよりもプロセスが複雑になる。その対応策として、損失地形の曲率情報を活用することで、収束を高速化するL-BFGS等が提案されている†4。
†4 ②のAdamとバッティングしており、どっちを選ぶのか問題が発生する。PINNsと同様に、Adam+L-BFGSが推奨されるかもしれない。
⑦ 最適化の不安定性防止
スプライン・ベースのアーキテクチャを扱う場合、最適化アルゴリズムは、大域的最小値ではなく局所的最小値に収束する傾向がある。この問題に対処するために、早期停止と学習率スケジュールが推奨されている。
2⃣ KANに固有の解決策
❶ スプラインベースの学習可能な重み
KANの重みは、MLPのように固定の線形変換ではなく、学習可能なスプライン関数である。これらの重みは、MLPと同様に、逆伝播などの勾配ベースの手法を用いて最適化される。ただし、KANで使用されるBスプライン関数を扱うには、特別な調整が必要である。
具体的には、学習中にスプライン・グリッドの更新を実施し、Bスプラインのノット・ベクトルの位置を調整することで、ネットワークの学習に合わせてスプラインを動的に適応させる。
❷ 分散保存初期化†5
KANモデルでは、安定した学習を保証するために、スプライン係数を慎重に初期化する必要がある。分散保存初期化は、層間の活性化関数の分散を維持するためによく用いられる。これにより、最適化中にモデルが勾配消失や勾配爆発の影響を受けないことが保証される。
†5 Variance-Preserving Initialization。正式な訳語はないと思われる。ちなみに、CNNはランダム初期化、RNNは直交初期化または恒等初期化を採用することが多い、とされる。
❸ 残差活性化関数†6
KANは学習中の収束性を向上させるために、残差活性化関数を用いることがある†7。これは、普通の活性化関数†8と学習済みスプライン関数の組み合わせである。この構造は、収束の加速と勾配消失の問題の軽減に効果があることが実証されている(CNNで使用される)残差接続に着想を得ている。
この構造は、活性化関数によって非線形性を導入し、スプライン関数はデータ内のより複雑で細粒度の関係をモデル化する。これらを組み合わせることで収束性が向上し、KANは学習中にスムーズに学習し、両方の要素を効果的にバランスさせることができる。
†6 Residual Activation Function。正式な訳語はないと思われる。
†7 KAN は、タスク(の複雑さ)に応じて、活性化関数を調整できることも、長所としてあげられる。
†8 [*22]では、例として、SiLU(Sigmoid-weighted Linear Unit)が上げられているが、ReLUでも何でも良い(はず)。 普通の活性化関数は残差活性化関数において、バックボーンとして機能する(という理解)。なお、SiLUは、Swishとも呼ばれる。
➍ 計算を高速化するための基底関数
Bスプラインは計算コストが高い場合があるため、FastKANなどのKANの派生型では、Bスプラインが、効率的なRBF(Radial Basis Function:動径基底関数)に置き換えられている(正確には、ガウシアンRBF)。これにより計算の複雑さが軽減され、高速化される。
(3) KANのバリアント
1⃣ チェビシェフKAN(cKAN)
関数近似において、Bスプライン関数の代わりにチェビシェフ多項式を用いたKAN。非線形関数の近似精度と収束性が向上する、とされる。チェビシェフPIKAN(cPIKAN)については、こちらを参照。
2⃣ テンポラルKAN(TKAN)及びMTKAN
TKANは、時系列データ処理向けに開発されたKANである。単変量時系列データ用に設計されたTKANは、非線形関係に動的に適応して複雑な時間的パターンを捕捉する、学習可能な単変量活性化関数を利用しており、時間の経過に伴う変化を効果的に処理できる。財務予測やエネルギー需要予測で有用とされる。
MTKAN は、多変量時系列データを処理できるように拡張されたTKANである。TKAN を基盤として、関連するタスク間でのマルチタスク学習を可能にする共有ネットワーク構造を導入している。MTKANは、電力負荷予測や大気質モニタリングなど、多変量依存関係が不可欠なアプリケーションにおける予測で有用とされる。
3⃣ Wav-KAN
Wavは、ウェーブレットの意味である。Wav-KAN は、学習可能な活性化関数としてウェーブレット関数を組み込むことで、入力特徴量の非線形マッピングを可能にし、マルチスケールの空間スペクトル・パターンを効果的に捕捉する。このアプローチにより、Wav-KAN はさまざまなスケールで重要なパターンを分離し、重要な特徴を保持しながらノイズを除去する能力を高めることができる。
また、Wav-KANは連続ウェーブレット変換と離散ウェーブレット変換を用いることで、高周波成分と低周波成分の両方を捉え、MLPと比較して解釈性と堅牢性を向上させることができる(らしい)。
4⃣ FastKAN
関数近似において、Bスプライン関数の代わりにガウシアンRBFガウシアンRBF を用いたKAN。ガウス・カーネルを活用することでパターン認識などの分野で近似プロセスを加速する、とされる。また、グラフや表形式のデータを扱うタスクでは、解釈可能性とパラメータ効率において、MLPよりも優れていることが実証されている(らしい)。
5⃣ グラフKAN(GKAN)
GKANは、KANをグラフ構造データに拡張する。グラフ・エッジに学習可能な単変数関数を導入することで、GKANは、グラフ畳み込みネットワーク(GCN)の固定された畳み込み構造を置き換える。GCNは、グラフ内の局所近傍から特徴量を反復的に集約および変換することで動作し、特徴量とグラフ・トポロジの両方を効果的に捕捉する。しかし、GCN は固定の畳み込みフィルタに依存しているため、複雑で異種のグラフを処理する際の柔軟性が制限される。
GCNの柔軟性に対する制限に対処するために、GKAN は 2 つアーキテクチャを導入する:アーキテクチャ1 は、KAN層を適用する前にノードの特徴量を集約し、学習可能な活性化関数が複雑な局所関係を捕捉できるようにする。アーキテクチャ 2 は、特徴量集約の前に、各層のノード埋め込みの間に KAN層を配置し、グラフ構造の変化に動的に適応できるようにする。この設定により、GKANは時間発展するグラフ構造全体にわたって、特徴量表現を最適化することで、大規模で異種混合のグラフデータに効果的に適応できる(らしい)。
6⃣ 有理KAN(rKAN)
rKANは、有理関数基底(具体的にはパデ近似と有理ヤコビ関数を採用)を使用して拡張されたKANである。rKANは、最適化された活性化関数と、より効率的なパラメーター更新メカニズムにより、モデルの精度と計算効率が向上する、とされる。
7⃣ SigKAN
SigKANは、時系列パスの重要な幾何学的特徴を捉えるパス・シグネチャ†9を組み込むことで、時系列データ予測機能を強化したKANである。SigKANのコア・アーキテクチャには、各入力シーケンスのパス・シグネチャを計算する学習可能パス・シグネチャ層が含まれている。このアーキテクチャにより、ネットワークはシーケンスの依存関係と複雑なパス構造を捉えることができる。金融モデリングや多変量予測などのタスクで効果を発揮する、とされる。
†9 パス・シグネチャに関しては、こちらを参照。
8⃣ ベイズKAN(BKAN)及びCoxKAN
KANの範囲を医療に拡大するベイズKAN(BKAN)は、医療診断に不可欠な、解釈可能で不確実性を考慮した予測を提供する。不確実性は、各ベイズ層に伝播して確率的な出力を生成し、医療診断における堅牢な意思決定をサポートする。
生存分析におけるCox比例ハザードモデルに特化したKANベースのフレームワークであるCoxKANは、自動特徴量選択と記号式抽出による高性能生存分析を容易にし、医療データセットにおける効果的なバイオマーカー同定と複雑な変数相互作用の発見を可能にする、とされる。
Ⅱ MLPベースPINNsとKANベースPINNsの比較
米ブラウン大学と米パシフィック・ノースウェスト国立研究所の研究者は、KANベースPINNs及びKANベース・ニューラル演算子(正確には、DeepONet🐾0)を、MLPベースPINNs及びMLPベース DeepONetと「可能な限り公正に」比較した論文[*13](以下、本論文)を発表した(24年6月5日@arXiv)。本論文では、KANベースPINNsはPIKAN、KANベース DeepONetは DeepOKANと呼称されている。また、MLPベースPINNsはバニラPINNsと呼んでいる。
〇×方式で結果を述べると、8戦中『PINNs・DeepONet4勝、PIKAN・DeepOKAN3勝、引き分け1』と思われる。ちなみに、[*1]で扱われたPINNsは、2次元ポアソン方程式を対象としており、結果は以下の通り:PIKANのL2相対誤差は10−7、PINNsのL2相対誤差は10−5。
🐾0 ニューラル演算子としてDeepONetが選ばれた理由は、本論文の著者がブラウン大学だからであろうと推測される。
❚❚ 事前整理
(1) モデルの略語
RBF・KAN=Bスプライン基底関数の代わりにガウシアン放射基底関数(RBF)を使用したKAN。レイヤー正規化を適用する。
チェビシェフ KAN=Bスプライン基底関数の代わりに、チェビシェフ多項式を使用したKAN。
cPIKAN=PINNsとチェビシェフKANの組み合わせ
LPIKAN=ルジャンドルPIKAN
JPIKAN=ヤコビPIKAN
HPIKAN=エルミートPIKAN
BーcPIKAN=ベイジアンcPIKAN
DeepOKAN=DeepONetと チェビシェフKANの組み合わせ
(2) RBAスキーム:残差ベースの注意(Residual Based Attention)に基づく重み更新スキーム
本論文では、以下のような問題意識の下、 「残差ベースの注意(RBA)に基づく重み更新スキーム(以下、RBAスキームと呼称)」を併用している:
問題意識⇒ ニューラルネットワークの学習における本質的な課題の1つは、累積損失関数を計算する際に、残差が見落とされる可能性があることである。ここで、累積損失関数は、残差の総和または平均を指す。残差とは、コロケーション点単位の誤差を意味する。
RBAスキームは、[*14]で導入されている。具体的には、コロケーション点iにおける、反復回数k+1回目の重みwik+1は、以下のように更新される:
wik+1=γ×wik+η|ri|/max(ri)
ここで、γは減衰率、ηは学習率(オプティマイザーの学習率とは別の値)、riはコロケーション点iにおける残差である。RBAスキームは、誤差が大きいコロケーション点の重みが大きくなるようなスキームとなっている。[*14]によると、L2相対誤差で10-5を達成できるらしい(本当?)。
(3) 人工粘性率
☞【3】(2)を参照。
❚❚❚ 比較結果
【0】不連続関数の近似
(0) 問題セットアップ
次のような不連続関数を対象に、MLPベースのニューラルネットワーク(以下、単にMLPと表記)とKANベースのニューラルネットワーク(以下、単にKANと表記)の近似能力を比較する。アーキテクチャの堅牢性を評価することが目的である。
y = 5+∑sin(kx)、x<0 (k=1~4)
y = cos(10x)、 x≥0
(1) 比較対象となったモデルのアーキテクチャ及び比較指標
1⃣ モデルのアーキテクチャ
MLPと、「KAN、チェビシェフKAN、修正チェビシェフKAN」を比較する。KANとは、Bスプライン基底関数を使ったオリジナルのKANを意味している。 修正チェビシェフKANとは、チェビシェフ層のフォワード パスが、y = (Φ◦tanh◦Φ)(x)と表現されるチェビシェフKANである。 Φは、チェビシェフ層である。修正チェビシェフKANを用意した理由は、チェビシェフ KANが学習中に、不安定性を示したためである(代替を用意した)。なお、Bスプライン関数、チェビシェフ多項式の次数は、3である。オプティマイザーは、Adam 。
比較の公正性を担保するために、MLPとKANにおいて、ニューラル ネットワーク・アーキテクチャは、「40 個のニューロンを含む 2 つの隠し層」で、共通させる。ただし、このアーキテクチャでは、チェビシェフ KAN と MLP の学習可能パラメーターの数は同桁であるのに対し、KANではパラメーターの数が 1 桁増加する。公平な比較を確実にするために、2 つの KAN アーキテクチャ(KAN-I と KAN-II)を使用している。KAN-I は MLP およびチェビシェフKAN と同じ数の層とニューロンを持つ。KAN-II は MLP およびチェビシェフ KAN と同じ数のパラメーターを持つ。
2⃣ 比較指標
L2相対誤差(%)と反復回数1回あたりの学習時間(ミリ秒)である。
(2) PINNsとPIKANとを比較した結果
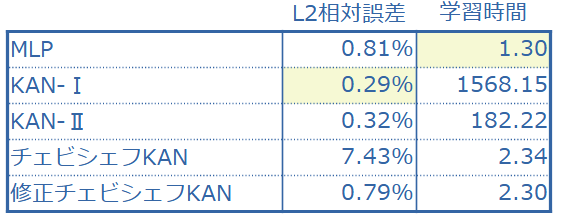
修正チェビシェフKAN と MLPは100,000 回の反復で学習を実施した。KAN-I と KAN-II については、それぞれ 20,000 と 25,000 回の反復で学習を停止した。
(3) 評価ーまとめ
チェビシェフKANを除いて、L2相対誤差のオーダーが10-3であり、まずまずといったところ。誤差だけを見ると、KAN-Ⅰが最良であるが時間がかかりすぎる。KAN-Ⅱでもまだ時間がかかりすぎる。総合評価では、MLPになるのではないだろうか。
結論◣ わざわざKANを選択する理由はないだろう。
【1】エネルギーを保存する動的システム
(0) 問題セットアップ
チェビシェフ KANが動的システムの位相空間をそのエネルギー(ハミルトニアン)を保存しながら効果的に予測できるかどうかを調査する。MLPは、このタスクに苦労している(らしい)。対応策として、MLP の学習プロセスにハミルトニアンを組み込むことが提案されている。そのような枠組みに対するチェビシェフ KAN の可能性を示すために、理想的な「ばね質量系」という、単純な例を採用する。
(1) 比較対象となったモデル及び比較指標
1⃣ 比較モデル概要
MLP の学習プロセスにハミルトニアンを組み込んだHNNと、HcKANとを比較した。HcKANとは、HNNのMLPをチェビシェフKANで置き換えたニューラルネットワークである。ただし、ここで言う
チェビシェフKANは【0】で導入された”修正チェビシェフKAN”であることに注意。学習中の不安定さから、導入された。チェビシェフ多項式の次数は3。学習率は1×10ー3で、オプティマイザーはAdam。
2⃣ 比較指標
定量的な比較指標はない。 ばね質量系の状態空間(q,p)をプロットした図、損失関数の収束履歴で(定性的に)比較している。qは位置、pは運動量を表している。
(2) PINNsとPIKANとを比較した結果
HNNによって予測された状態空間と実際の状態空間は、良好に一致している(汎化誤差が小さい)。一方、HcKANはHNNほど一致が良好ではない(汎化誤差が大きい)。それは、損失関数の収束履歴からも示唆される。
(3) 評価ーまとめ
結論◣ MLPの代わりにKANを選択する理由はないだろう。
【2】(2次元)ヘルムホルツ方程式
(0) 問題セットアップ
外力項を、波数a1、a2とsin(a1πx)、sin(a2πy)から生成されるある多項式の形で設定すると、2次元ヘルムホルツ方程式は、u(x,y)=sin(a1πx)sin(a2πy)という解析解を持つ。境界条件は、u(−1, y) = u(1, y) = u(x, −1) = u(x, 1) = 0とする。
(1) 比較対象となったモデルのアーキテクチャ及び比較指標
1⃣ 比較モデルのアーキテクチャ
2次元ヘルムホルツ方程式の分析は、下記3つの枠組みで、PINN(RBAスキーム採用、不採用)を、以下のPIKANと比較する:PIKAN(RBAスキーム採用、不採用)、cPIKAN(RBAスキーム採用、不採用)及びマルチグリッドPIKAN(Bスプラインのグリッド点を増やしたPIKAN)。
3つの枠組みとは、「パラメータ・ベースの分析、計算時間ベースの分析、複雑性ベースの分析」である。なお、マルチグリッドPIKANは、パラメータ・ベースの分析、でのみ使用される。
㈠ パラメータ・ベースの分析
すべてのモデル間でパラメータの数を、ほぼ一致させるアーキテクチャを採用する。PINNには16個のニューロンを持つ「2つの隠し層」があり、PIKANには10個のニューロンとk = g = 5を持つ「1つの隠し層」がある。ここで、kはBスプライン関数の次数。gは、グリッド点(あるいはノットベクトルと呼ばれる)の数。cPIKANには、8つのニューロンとk = 5を持つ「2つの隠し層」がある。この場合のkは、チェビシェフ多項式の次数である。
マルチグリッドPIKANで、グリッド点を増やす方法は以下の通りである:次数kは3に設定し、グリッド点の数gの初期値は5である。学習プロセスを3つのステージに分割して、600回の反復ごとに、グリッド点の数を2倍にする。
51 × 51 のコロケーション点のサンプル空間で、LBFGオプティマイザーを使用する。境界損失の重みは1、PDE損失の重みは0.01と設定する。RBAスキームは、重みの初期値を1に設定し、学習率は、1×10-4とする。
㈡ 計算時間ベースの分析
ここでは、より深いネットワーク (隠し層数4) と、より多くのコロケーション点(100 × 100)について PINN および cPIKANモデルを分析する。 パラメータ・ベースの分析では、 隠し層数2であった。
PINN および cPIKAN では、それぞれ隠し層あたり 100 および 32 のニューロンを使用する。
オプティマイザーは学習率スケジューラを備えたAdamを使用。学習率は、1×10-3 で開始し 1×10-4で終了する。2×105回の反復でネットワーク パラメーターを更新する。境界損失の重みは1、PDE損失の重みも1と設定する。PDE損失にのみRBAスキームを使用する。RBAスキームは、重みの初期値を0に設定し、学習率は、1×10-3とする。
㈢ 複雑性ベースの分析
問題の複雑性を高めるために、ヘルムホルツ方程式をより高い波数で解く。具体的には、a1 = a2 = 6とする。a1及びa2は、(0)1⃣を参照。なお、㈠及び㈡では、a1 =1、a2 = 4であった。
PINN では、1 層あたり 128 個のニューロンを持つ 6 つの隠し層を使用。cPIKAN では、5 層、32 個のニューロン、チェビシェフ多項式の次数k = 5 を使用する。オプティマイザーはAdamでスケジューラ付き。1×10-3で開始し、5×10-5で終了する。5×105回の反復でネットワーク パラメーターを更新する。境界損失の重み=PDE損失の重み=1と設定し、PDE損失にのみRBAスキームを適用する。RBAスキームの、重み初期値は0で、学習率は、1×10-3 である。
2⃣ 比較指標
L2相対誤差(%)と反復回数当たりの学習時間(ミリ秒)で比較する。
(2) PINNsとPIKANとを比較した結果
(3) 評価ーまとめ
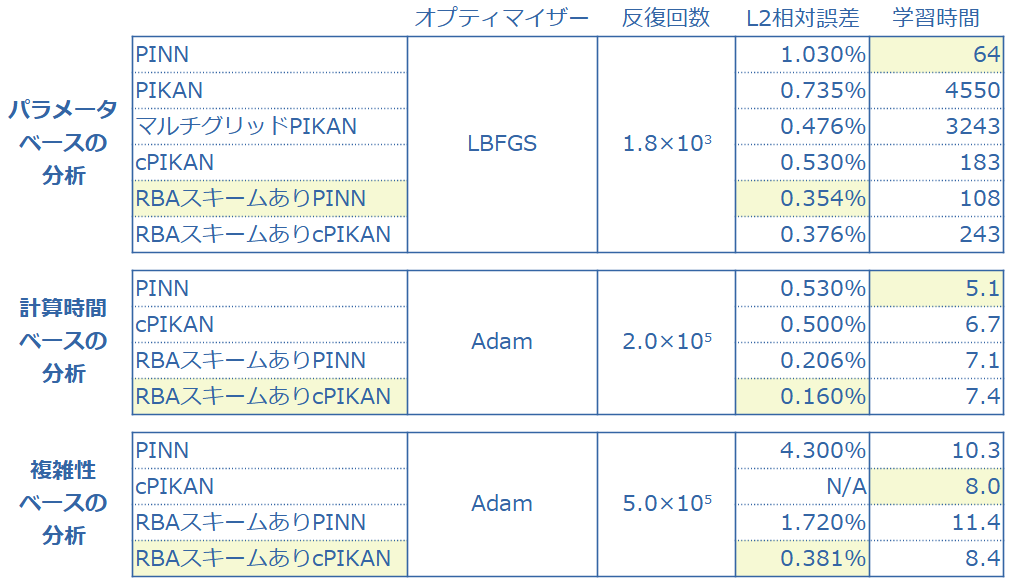
水準のみの総評:PIKAN系のL2相対誤差のオーダーは、概ね(1例を除いて)10-3であり、まずまずといったところ。
㈠ パラメータ・ベースの分析
まず、PINNのL2相対誤差のオーダーが10-2なので、不満足な結果。PIKANで10-3になるが、学習時間がかかり過ぎるのでダメ。そこでcPIKANにすると、計算時間とL2相対誤差も、いい感じになる。ただ、RBAスキームを使うとPINNのL2相対誤差が0.354%と最良になる。つまり、ベストパフォーマーはRBAスキーム採用PINNということになる。
㈡ 計算時間ベースの分析
コロケーション点を増やし(約4倍)、反復回数を増やし(約100倍)、隠し層の数を増やし(2倍)た、ので、全体的に良い結果が出て当然。ただ、ベストパフォーマーがRBAスキーム採用cPIKANに交代した。
㈢ 複雑性ベースの分析
高い波数でヘルムホルツ方程式を解くというケースである。このケースでは、RBAスキーム採用cPIKANのL2相対誤差が最良で、唯一10-3のオーダーである。つまり、複雑性の高いケースでは、RBAスキームは必要であるものの、cPIKANが唯一使えるモデルということになる(本論文では、それを示したかったと思われる)。ただ、RBAスキームなしのcPIKANは発散しているという結果は、不安を招くだろう。
(4) 感度分析
ただ、RBAスキームなしのcPIKANは発散しているという結果は、不安を招くだろう・・・と本論文の著者も思ったのだろう。cPIKAN感度分析を実施している。具体的には、隠れ層の数 nℓと多項式次数 k の影響を調べている。
その結果は、「k または nℓを増やすと cPIKAN のパフォーマンスは向上するものの、モデルが不安定になる」。ただ、この不安定性は倍精度(float 64)を使用することで、回避されるとする。回避の意味は、モデルが不安定になる傾向は変わらないが、より大きいk または nℓを使ってモデルを学習できるという意味である。ただし、その場合、計算コストが増加することは言うまでもない。
結論◣ 2次元ヘルムホルツ方程式に関しては、RBAスキーム採用cPIKANがベストパフォーマーということで良いのだろう。つまり、MLPをKANで置き換える価値がある。
【3】(2次元定常非圧縮)ナヴィエ・ストークス方程式ーNS方程式
(0) 問題セットアップ
蓋駆動キャビティ流れ。この流れは、よく知られたベンチマークケース(定番)であり、数値計算の検証で頻繁に使用される。
レイノルズ数(Re) = 400 および Re = 2000 でシミュレーションを実行した。Re = 2000 は、教科書的には層流から乱流に遷移する境目であり、(流体力学的には)特別な意味を持つ。コロケーション点の数は、Re = 400で1×104、Re = 2000で2×104。エポック数は、Re = 400で9×105、Re = 2000で4×105。
(1) 比較対象となったモデルの概要及び、比較された量と比較指標
1⃣ 比較モデル概要
ガウス基底ベース及び、「チェビシェフ、ヤコビ、ルジャンドル、およびエルミート」多項式ベースの PIKANを、バニラPINNと比較した。ルジャンドル多項式やチェビシェフ多項式は、ヤコビ多項式の特殊な場合である。なお、ヤコビ多項式 {Pn(α,β)(x)}のα,βは、ともに1と置いている。 オプティマイザーはAdamを使用。
2⃣ 比較量と比較指標
比較された量は、流速(x方向の流速uと、y方向の流速v)と圧力p、並びに反復回数1回あたりの学習時間(ミリ秒/回)。流速と圧力の、比較指標はL2相対誤差(%)である。グランドトルゥースは、高性能ソルバーによる数値解である。
人工粘性率の導入は、形の上ではシンプルであり、(NS方程式上も、PDE損失上も)動粘性率を、「動粘性率+人工粘性率」で置き換える。理論的な根拠は、「人工粘性率は、(数値計算における離散化を原因とする)エントロピー等式🐾2の破れを補償している」[*16]ということらしい。
本論文では、学習可能パラメータとして、人工粘性率を具体的に推論する式が提示されている([*15]における式とは異なる)。
🐾1 [*15]で具体的に言うと、Re=1000。
🐾2 ここでいうエントロピー等式とは、∂tS + ∇・(uS)= 0であり、一般的には不等式(≥)で表される。Sはエントロピーで、uは適当な流速ベクトルである。速度ベクトル場と運動量ベクトル場が滑らかな場合は、等式が成り立つ(らしい)。
(3) PINNsとPIKANとを比較した結果
(4) 評価ーまとめ
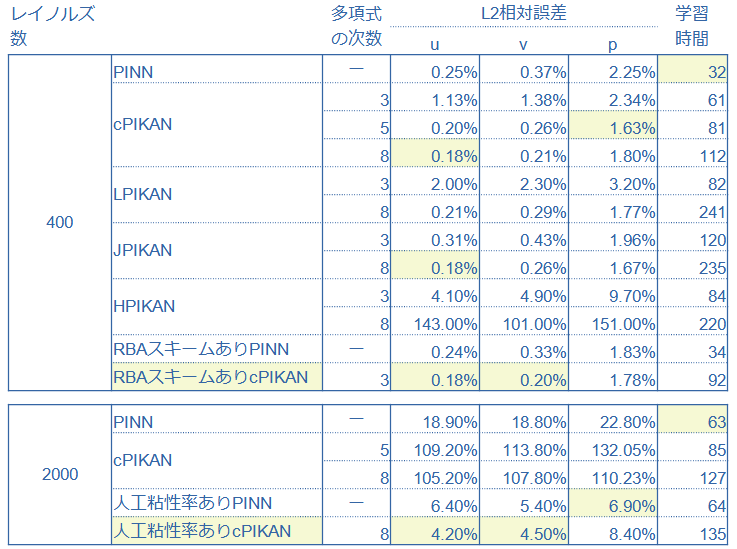
㈠ 概ね、多項式の次数が上がるにつれて、L2相対誤差は小さくなる(例外あり、特にエルミートPIKANは顕著)。なお、エルミートPIKAN(次数8)のL2相対誤差は、100のオーダーなので、真剣にヤバい。
㈡ RBAスキームは、PINNsにはあまり効かない。一方、PIKANには、効いている。
㈢ PINNsもcPIKANも、Re=2000では使い物にならないが、PINNsの方がマシ。L2相対誤差で言うと、PINNsが10-1のオーダーで、cPIKANが100のオーダー。高Re数(非線形性が強い)で性能が低いというPINNsの性質が増大している。ただし、人工粘性率を導入すれば、cPIKANのL2相対誤差は、10-2のオーダーと劇的に改善する。
㈣ (反復回数1回あたりの)学習時間は、PIKANが数倍多くかかる(その程度で済んでいる)。一方、パラメータ数は数分の一に抑えられる。
結論◣ L2相対誤差及び、学習時間の両軸で評価したとき、チェビシェフPIKANが最も優れている。人工粘性率の導入は、効く。特にPIKAN(cPIKAN)には劇的に効く。
【4】(空間次元1+時間次元1の2次元)非線形アレン・カーン方程式
(0) 問題セットアップ
アレン・カーン方程式は、Raissi他によるPINNsのオリジナル論文[*17]にも登場する由緒正しき方程式である。[*17]でアレン・カーン方程式は、「反応拡散系の分野でよく知られた方程式である。この方程式は、秩序-無秩序転移を含む多成分合金系における相分離の過程を記述する」と説明されている。
本論文で扱うアレン・カーン方程式は、[*17]と全く同じである🐾3。
∂tu-D∇2u+5(u3-u)
D = 1 × 10-4、t ∈ [0, 1]、x ∈ [−1, 1]
初期条件:u(x,0)=x2cos(πx)
境界条件:u(-1,t)=u(1,t)=-1
🐾3 [*17]では、ディリクレ境界条件に加えて、ノイマン境界条件∂xu(t, −1) = ∂xu(t, 1)、も課されている。単なる誤植?
(1) 比較対象となったモデル概要及び比較指標
1⃣ 比較モデル概要
PIKANは、以下の3種類:PIKAN(Bスプラインを使ったオリジナルKANベースのPIKAN)、(RBAスキームを使わない)cPIKAN、RBAスキームを使ったcPIKAN。PINNsは、RBAスキームを使ったPINNs。
学習率5×10−4のAdamオプティマイザーを使用。学習は、150,000回の反復まで単一のバッチ学習として実行された。
2⃣ 比較指標
L2相対誤差(%)と反復回数1回あたりの学習時間(ミリ秒)。
(2) PINNsとPIKANとを比較した結果
(3) 評価ーまとめ
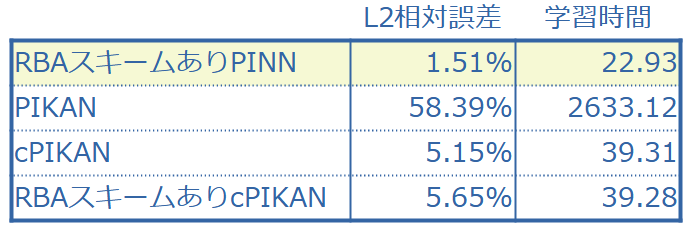
PIKANは全くダメ。他もL2相対誤差が10-2なので、宜しくない。学習時間も長い。ザックリ言って、本論文の結果を見る限り、非線形アレン・カーン方程式は難しいということになるだろう。しかし・・・
全く同じセットアップのはずである[*17]の結果は、PINNのL2相対誤差が6.99×10−3である。本論文では、RBAスキーム採用PINNのL2相対誤差が1.51×10−2であり、非常に不思議である。
結論◣ PINNs(ただしRBAスキーム採用)がベストパフォーマー。つまり、MLPをKANで置き換える価値はない。([*17]の結果は、この結論に影響しない)
【5】不確実性定量化を伴う微分方程式
(0) 問題と計算環境
1⃣ 問題セットアップ
ここでは、「不確実性定量化(UQ)を伴う微分方程式を解く」という、これまでの事例とは異なったケースを扱う。微分方程式自体は、1次元定常反応拡散方程式
D∂xxu+κ×tanh(u) = f
D:拡散係数=0.01
κ:反応率 ・・・未知(なので要推定)
f:ソース項
であるが、ノイズの多いデータで解くというセットアップである。具体的には、ノイズの多いuとfのデータが与えられた場合に、不確実性を伴うuとκを推定することである。つまり、PINNsが得意な逆問題、となっている。
処方箋は、以下の通りである:cPIKANにベイジアン・フレームワークを装備し、ハミルトニアン・モンテカルロ法(HMC)を使用して、データDが与えられたときのパラメータθの事後分布p(θ|D)を推定する。
2⃣ ノイズの多いuとfのデータ生成
u(x) = sin3(6x), x ∈ [−0.7, 0.7]をサンプリングして、1次元定常反応拡散方程式に代入することで、ノイズなしのfを生成する。u(x)には、「平均0、標準偏差0.05」の加算性ガウスノイズが加えられてノイズの多いuが生成される。ノイズなしのfには、「平均0、標準偏差0.1」の加算性ガウスノイズが加えられてノイズの多いfが生成される。
(1) 比較対象となったモデル概要及び比較指標
1⃣ 比較モデル概要
ベイジアンPINNとベイジアンcPINN(B-cPIKAN)。チェビシェフ多項式の次数は3。B-cPIKANの事前分布は、「平均0、標準偏差0.5」の独立ガウス分布になるように選択され、B-PINNの事前分布は、「平均0、標準偏差1」の独立ガウス分布である。
ベイジアンPINNとB-cPIKANの事後分布からサンプリングするためにHMCが使用される。HMCは、初期ステップサイズ0.01、リープフロッグのステップサイズが50。バーンイン期間のサンプル数を2,000、事後サンプル数を1,000に設定されている。
2⃣ 比較指標
uはL2相対誤差(%)、κは絶対誤差(%)を使用。加えて、反復回数1回あたりの学習時間(ミリ秒)。
(2) PINNsとPIKANとを比較した結果

(3) 評価ーまとめ
ベイジアンPINN、B-cPIKANともにL2相対誤差及び絶対誤差が10ー1なので、全く不十分。逆問題へのケアが足りないのか?
結論◣ (いずれにしても)MLPベースをKANベースに置き換える価値はないだろう。
【6】(1次元)バーガース方程式|ニューラル演算子
(0) 問題セットアップ
これまでは、ニューラルネットワークを扱っていたが、ここからはニューラル演算子を扱う。ここでは、周期境界条件付き(1次元)バーガース方程式の解演算子を学習する。解演算子とは、ニューラル演算子が学習する、関数空間間の非線形演算子(しばしばGというアルファベットが割り当てられる)のことを言う。具体的には、時刻t=0における任意の初期関数u0を、時刻t = 1におけるバーガース方程式の解u1に写像する非線形演算子Gを学習する。
さらに、ノイズの多い入力関数に対する堅牢性をテストする。ネットワークはクリーンな(ノイズのない)データで学習され、ノイズの多いデータでテストされる。
(1) 比較対象となったモデル及び比較指標
1⃣ 比較モデル
DeepONetとDeepOKAN。DeepOKANのKANは、チェビシェフKANでチェビシェフ多項式の次数は 3。DeepOKANはネットワーク・アーキテクチャが異なる2種類が用意されている。DeepONetのネットワーク・アーキテクチャは、ブランチ ネットが[128, 100, 100, 100, 100]、トランク ネットが[4, 100, 100, 100]。どちらも tanh活性化関数を備えている。DeepOKAN1は、ブランチ ネットが[128, 100, 100, 100, 100]、トランク ネットが[4, 100, 100, 100]。つまり、DeepONetと同じ。DeepOKAN2は、ブランチ ネットが[128, 50, 50, 50, 50]、トランク ネットが[4, 50, 50, 50, 50]。
2⃣ 学習について
学習とテストには、1000個のu0と200個のu(・,t=1)が使用される。学習データの平均と標準偏差に基づいて、演算子ネットワークの出力が正規化される(データ正規化)。
オプティマイザーはAdamで、DeepONet の学習率は、10 万回の反復で 1×10-3、さらに 10 万回の反復で1×10-4。DeepOKANでは(1、2ともに)、10 万回の反復で1×10-4、さらに 10 万回の反復で1×10-5である。また、過学習対策として、重み1×10-5 のL2 正則化器が、 DeepONetとDeepOKANの両方に、追加されている。
3⃣ 比較指標
L2相対誤差(%)と反復回数1回あたりの学習時間(ミリ秒)。
(2) DeepONetとDeepOKANとを比較した結果
ノイズは、平均0のガウス・ノイズを加えたu0(xi)を考えることによって導入する。xiは、入力関数と出力関数が解かれる一様なグリッド点である。

(3) 評価ーまとめ
L2相対誤差の水準が10-2であり、宜しくはない。優劣をつけるとDeepOKAN1のL2相対誤差が最も小さい。堅牢性は、DeepONet及びDeepOKANともにあるという結論であろう。比較して優劣を付けると、DeepONetの方が、ノイズにはより堅牢であると思われる(本論文は、DeepOKANの方が堅牢と主張している)。それは、ノイズを追加したことによるL2相対誤差の悪化は、DeepONetの方が小さいからである。ノイズなしのL2相対誤差自体、DeepONetは大きいが、変化率は小さい。
結論◣ L2相対誤差の水準に不満は残るが、MLPベースをKANベースに置き換える価値はある、と言って良いだろう。
【7】多孔質媒体を通る 2次元定常流れ|ニューラル演算子
(0) 問題セットアップ
1⃣ 概要
ここでは、定常ダルシー則で記述される、多孔質媒体を通る 2次元定常流れについて検討する。透水係数λ(x,y)の対数log(λ)を、水頭u に写像する解演算子Gを学習する。
2⃣ 式で表すと・・・
式で表すと、次のようになる。
∇(フラックス)=ソース項
フラックス=透水係数×水頭勾配 ≐ λ(x,y)×∇u(x,y)、x, y ∈ (0, 1)
ソース項=ー30
境界条件:u(0, y) = 1, u(1, y) = 0 ※uは、水頭。
∂nu(x, 0) = ∂nu(x, 1) = 0
3⃣ log(λ)のサンプリングについて・・・
透水係数の対数log(λ)は、平均が0でガウシアン・カーネルK(x,x’;y,y’)を持つガウス過程のカルーネン・レーベ展開からサンプリングされる。ちなみに、ガウシアン・カーネルのハイパーパラメータ(ここでは相関長)は0.25である。
(1) 比較対象となったモデル及び比較指標
1⃣ 比較モデル
解演算子 G を学習するために、DeepONet と DeepOKAN をそれぞれ 1 つずつ使用する。
DeepONet 及びDeepOKAN のネットワーク・アーキテクチャは、ブランチ ネットが[961, 100, 100, 100, 100]、トランク ネットが[2, 100, 100, 100] である。DeepONet は活性化関数として tanh を持つ。DeepOKAN におけるチェビシェフ多項式の次数は 3 である。
2⃣ 学習について
log(λ) と u を表すために 31 × 31 の均一グリッドを使用し、カルーネン・レーベ展開の最初の 120 個の主要項は保持される。学習とテストを実行するために、10,000 個のlog(λ) と 1,000個のu が使用される。パフォーマンスを向上させるために、学習データの平均と標準偏差に基づいてネットワークの入力と出力の両方を正規化する。
オプティマイザーは、ともにAdamを採用。DeepONet の学習率は 10 万回の反復で1×10-3、さらに 10 万回の反復で1×10-4。DeepOKAN の場合は 10 万回の反復で1×10-4、さらに 10 万回の反復で1×10-5。過学習を避けるために、DeepOKANに重み係数1×10-4のL2正則化を適用する。
(2) DeepONetとDeepOKANとを比較した結果

(3) 評価ーまとめ
L2相対誤差は、10-2オーダーであり、宜しくはない。比較するとDeepONetの方が優れている(学習時間は言うまでもない)。ただ、堅牢性に関しては、DeepOKANの方が優れている。
結論◣ MLPベースをKANベースに置き換える価値はない、と言えるだろう。
❚❚❚❚考察
(1) MLPとKANの比較では、例えば、シンガポール国立大学の研究者による研究[*5]がある。「シンボリック回帰式(表現)、機械学習(タスク)、コンピューター・ビジョン(画像認識)、自然言語処理(NLP)、音声処理」において、MLPとKANの”公正な”比較を行った結果は、「シンボリック回帰式(表現)以外は、MLPがKANに勝った」(と主張)。※既述
MLPベースPINNsとKANベースPINNsの比較では、例えば、中国・清華大学他の研究者による研究[*7]がある。「マルチスケール問題、特異点問題、応力集中問題、非線形超弾性問題、不均質問題、複雑形状問題」などに対して、MLPベースのPINNsとKANベースのPINNsを比較した結果、「複雑形状問題を除き、精度と収束速度に関してMLPを大幅に上回ることが実証された」(と主張)。※既述
本論文の結果をザックリ言うと、4勝3敗1分けでMLPベースPINNsが勝った、という内容であった。これをもって、KANは大したことないと見限るのは合理的ではないだろう。
(2) 例えば、高波数の2次元ヘルムホルツ方程式を解くケース(複雑性ベースの分析)で、cPIKANは収束すらしない。しかし、RBAスキームを使うと劇的に改善し、RBAスキームを使ったPINNsより(RBAスキームを使ったcPINKANの)L2相対誤差が小さくなる。乱流域のNS方程式を解くケースでも、cPINKANはPINNsより低性能であるが、人工粘性率を導入すると、人工粘性率を導入したPINNsより(人工粘性率を導入したcPIKAN)のL2相対誤差が小さくなる。
つまり、KANベースのPINNsを考える→つまづく→解決策をひねり出す→より良い方法が見つかる、という好循環が生まれた。広く言えばPINNsのフレームワークというか、広義のPINNsファミリー(物理学ベースのデータ駆動型モデル)の性能がアップした、と言えるだろう。研究とは、まさに、そういうものであろう。
(3) 本論文では、PINNsに拡張した情報ボトルネック法を使って、(RBAスキーム採用・不採用)PINNs、(RBAスキーム採用・不採用)cPIKANの学習ダイナミクスを分析している。対象は明示されていないが、2次元ヘルムホルツ方程式(複雑性ベースの分析)であろう。RBAスキーム採用cPIKANが最も早く全拡散段階に移行し、L2相対誤差が最も小さい事実と符合する。また、RBAスキーム採用・不採用に関わらずPINNsは、全拡散段階でもSNR(信号対雑音比)の振動が激しい。
IEEE🐾1のメンバー及びフェローを名乗る研究者が、「電力システム・アプリケーション向けに(初めて)PIKANを適用」した論文[*18](以下、本論文)を発表した(24年8月13日@arXiv)。PINNsと比べて、「より小さなニューラル ネットワーク・サイズで、電力システムの微分代数方程式を解く際の精度が向上した」と主張する。数理的に言うと、動揺方程式と呼ばれる微分代数方程式が支配方程式である対象系に、PIKANを適用する。
🐾1 Institute of Electrical and Electronics Engineers。
【1】本論文の主張
本論文は、PIKANとPINNの比較において、以下を主張する🐾2。尚、❶一機無限大母線(SMIB)、❷4母線2発電機(4B2G)🐾3である:
(1) 動揺方程式🐾4のパラメータが変動しないケース➡ 電気角🐾4の相対予測誤差(中央値)は、❶約21%、❷約79%改善した。
(2) パラメータ(慣性定数と制動定数)が変動するケース、かつ❷のみ➡ 慣性定数の相対予測誤差(中央値)は、50~60%改善。制動定数の相対予測誤差(中央値)は、40~50%改善した🐾5。
さらに、以下を主張する:
(3) PIKANはPINN のネットワークサイズの、❶41%、❷58%、のみを使用したにも関わらず、より高い精度を達成した。
(4) PIKANは、従来の深層ニューラルネットワークと比較して、学習データ ポイントのわずか 10% しか必要とせずに、同等またはそれ以上のパフォーマンスを達成できる。
(5) 境界値に加えて、境界値の時間微分値🐾6を併せて、(PINNsフレームワークにおける)境界損失を構築すると、PINNs及びPIKANの精度が向上する。
🐾2 本論文の結果を、そのまま掲示しているわけではないことに注意。本論文で得られた結果を要約するために、簡単な計算を行って、その計算結果を書いた。
🐾3 【2】(1)参照。なお、本論文中に、4B2Gという略語は使用されていない(本稿で便宜上、使った)。
🐾4 【2】(2)参照。
🐾5 本論文中には、箱ひげ図が描かれているだけなので、図から読み取って計算結果を書いた。
🐾6 境界値は電気角。境界値の時間微分値は、電気角速度になる。なお、(この文脈で)境界値と言及した場合は、初期値を含む。
【2】事前整理
(1) 母線(busあるいは bus line)
母線とは、受変電設備の主回路となる電器導体である。無限大母線とは、大容量の電力系統を表現するモデルである。無限大母線では、電圧及び周波数は、常に一定と仮定される。一機無限大母線(SMIB)とは、発電機1機と無限大母線で構成される電力系統モデルで、最も基本的な系統構成である。
(2) 動揺方程式(swing方程式)
1⃣ 数理的な説明
発電機回転子の運動方程式を動揺方程式と呼ぶ。動揺方程式は、
慣性定数×電気角の2階時間微分+制動定数×電気角の1階時間微分=機械的入力🐾7ー電気出力🐾8
である(表現上のバリアントあり)。 電気角の1階時間微分=電気角速度である。
発電機による発生する交流電力は正弦波形で表現できる。正弦波形は単位円上の回転運動としても表現できるので、正弦波形を表現するパラメータとして、角度を導入することもできる。交流電力の正弦波形を表現する角度パラメータを電気角と呼ぶ。
🐾7 機械的入力=蒸気タービンや水車などからの機械的なトルク。
🐾8 電気出力=電気的なトルク。
2⃣ 実用的な説明ー動揺方程式が何の役に立つのか?
今後さらに系統連系されると予想される再生可能エネルギーには、発電機が持っている、慣性や同期化力(同じ速度で回ろうとする力)などの機械特性はない。このため、系統セキュリティ🐾9を保持することが技術的に難しい。そこで、数理的に、「仮想発電機」を構築するという解決策が考案された。動揺方程式で記述される数理モデルが、「仮想発電機」である。
要するに、ザックリ言えば、動揺方程式のパラメータ(慣性定数と制動定数)を求め、変数(電気角)を制御することは、スマートグリッドの実現に資するいうことになる。
🐾9 (落雷などによる自然災害由来の停電といった)系統事故時に周波数を一定に保つ、電圧を一定に保つ、系統安定度を維持することを、系統セキュリティと呼ぶ[*19]。系統安定度維持とは、供給側と需要側とのトルクを一定の幅でマッチさせることを意味する。
【3】本論文のセットアップ
(1) データセット
0⃣ 環境
PIKAN の学習と性能テストは、64 GB RAM を搭載した Intel Xeon(R) Gold 6248R CPU @3.00 GHz × 48 Windows ベース サーバーで PyTorch で実施した。SciPy を使用して実装された時間領域シミュレーションを利用して、データセットは生成された。
1⃣ SMIBの学習及びテスト・データセット
電気角と電気角速度の初期値がそれぞれ 0.1 rad と 0.1 rad/s であると想定した。機械的入力の値は 0.08 p.u. 🐾10から 0.18 p.u. の範囲である。データは、時間ウィンドウ [0, 20(秒)] にわたって 0.1 秒の時間ステップで生成される。このケース設定では、100 のデータセットを生成した。
🐾10 本論文においては、母線電圧の大きさを1とした場合の相対値を表す、相対単位。
2⃣ 4B2Gの学習及びテスト・データセット
システムは t = 0 で平衡状態にあると想定する。次に、t > 0で、一定の入力信号 = a × [0.1, 0.2, −0.1, −0.2] p.u. でシステムを摂動する。aは0.5 から 9.5 まで、0.5 刻みで変移させる。各データセットについて、学習データとテストデータは、0.1 秒刻みで 0 秒から 5 秒までの時間間隔で構成される。データセットには、各時間ステップにおける、(各バスに対する)電気角と、対応する入力信号が含まれる。
(2) モデル・アーキテクチャ
1⃣ 動揺方程式のパラメータが変動しないケース✚❶SMIB
[2、5、1]形状の2層 KANを採用したPIKANを適用する。各学習ステップでは、ランダムにサンプリングされた時間と機械的入力が KAN に入力され、損失関数を最小化するように学習される。ノット・ベクトル(あるいはグリッド)は10に設定され、Bスプライン多項式の次数は3 に設定された。境界値を与える点の数は40、コロケーション点の数は800。オプティマイザーは定かではないが、AdamかLBFGS。
2⃣ 動揺方程式のパラメータが変動しないケース✚❷4B2G
[5, 10, 4]形状の2層KANを採用したPIKANを適用する。各学習ステップでは、ランダムにサンプリングされた時間と機械的入力がKANに入力され、損失関数を最小化するように学習される。グリッドは5に設定され、次数は3 に設定された。境界値を与える点の数は80、コロケーション点の数は4000。オプティマイザーは定かではないが、AdamかLBFGS。
3⃣ 動揺方程式のパラメータが変動するケース✚❷4B2Gのみ
2⃣と同じ。ニューラル ネットワークの重みはランダムに初期化される。推論(予測)は、20 回実行される。
(3) 損失関数による違い
本論文では、境界損失を電気角のみで構築した場合と、電気角に加えて電気角速度で構築した場合の2パターンを考える。前者の損失関数を採用したPINNsをPINN-Ⅰ、PIKANをPIKAN-Ⅰと呼称している。後者の損失関数を採用したPINNsをPINN-Ⅱ、PIKANをPIKAN-Ⅱと呼称している。
【4】比較結果
(0) 評価指標
電気角の相対予測誤差は、(実測値ー予測値)/実測値を、L2ノルムで計算する。パラメータ(慣性定数と制動定数)は、L1ノルムで計算する。
(1) 動揺方程式のパラメータが変動しないケース
1⃣ SMIB
PIKAN-Ⅰの電気角の相対予測誤差は、最大値1.06%、最小値0.014%、中央値0.688%である。PIKAN-Ⅱは、最大値1.53%、最小値0.184%、中央値0.633%である。最大値・最小値だけを見れば、PIKAN-Ⅰの方が優れているが、中央値では、若干PINN-Ⅱが勝る。
PINN-Ⅰは、最大値2.30%、最小値0.057%、中央値1.96%。PINN-Ⅱは、最大値1.48%、最小値0.206%、中央値0.800%である。PINN-Ⅰのパフォーマンスは低いが、PINN-Ⅱはそれほど悪くはない。PINNsは、損失関数の違いによる効果が大きい。
【1】主張(1)における(相対予測誤差の)改善率❶約21%は、0.800%と0.633%から計算している。改善率=(PINNsの相対予測誤差中央値-PIKANの相対予測誤差中央値)/PINNsの相対予測誤差中央値、である(以下、同じ)。
2⃣ 4B2G
PIKAN-Ⅰの電気角の相対予測誤差は、最大値4.85%、最小値0.043%、中央値4.64%である。PIKAN-Ⅱは、最大値1.94%、最小値0.040%、中央値0.538%である。最小値はPIKAN-ⅠとPIKAN-Ⅱで、ほぼ変わらないが、最大値は、大きく変わる。中央値に至っては、およそ1桁違う。SMIBではPIKAN-Ⅰの方がバランスがとれているという見方も出来るだろうが、4B2Gでは、話にならない。両者の違いを見ると、PIKANは信頼性に欠ける、という見方もできるだろう。
PINN-Ⅰは、最大値6.35%、最小値0.151%、中央値5.03%。PINN-Ⅱは、最大値5.98%、最小値0.076%、中央値2.59%である。PINN-Ⅰのパフォーマンスは(やはり)低いが、PINN-Ⅱはそれほど悪くはないように思える。また、SMIBと4B2Gの比較において、損失関数の違いが与える影響はコンシステントであるように思える(最小値に関しては、やや苦しい主張になるが・・・)。
【1】主張(1)における改善率❷約79%は、2.59%と0.538%から計算している。
(2) 動揺方程式のパラメータが変動するケース、かつ❷のみ。
箱ひげ図から読みとった値から計算した改善率を、平均して、最終的な改善率を算出している。慣性定数に対する【1】主張(2)における(最終的な)改善率50~60%は、以下のように算出した:2つの改善率30.8%(M1)と78.3%(M2)の平均値54.5%から幅をもたせて、50~60%とした。繰り返しになるが、30.8%や78.3%は、箱ひげ図から読みとった値から計算していることに注意(本論文中に数字は明示されていない)。
制動定数に対する【1】主張(2)における(最終的な)改善率40~50%は、以下のように算出した:4つの改善率47.1%(D1)、42.9%(D2)、56.7%(D3)、25.0%(D4)の平均値42.9%から幅をもたせて、40~50%とした。
(3) 学習時間
1⃣ SMIB
PIKAN-Ⅰ=87.5ミリ秒/回、PIKAN-Ⅱ=130ミリ秒/回。 PINN-Ⅰ=0.54ミリ秒/回、PINN-Ⅱ=3.41ミリ秒/回。系統セキュリティ保持には時間制限がある。この時間差はナンセンスではないか。時間差を抜きにしても、SMIBでPINN-Ⅱの代わりにPIKANを使うメリットはないように思える。
2⃣ 4B2G
PIKAN-Ⅰ=1225ミリ秒/回、PIKAN-Ⅱ=1390ミリ秒/回。 PINN-Ⅰ=2.89ミリ秒/回、PINN-Ⅱ=3.78ミリ秒/回。系統セキュリティ保持を念頭に置けば、時間差は許容範囲外か?
【5】考察
(1) 【4】(1)2⃣で記述した通り、PIKANは信頼性に欠ける、という見方もできるだろう。つまり、本論文で示された少ないシミュレーション事例からは、PIKANがPINNsより精度が良いという判断は出来ないように思える(たまたまの可能性を、排除できないように思われる)。
ちなみに、本論文は、アプリオリには次のような当たりをつけている(後付けの理屈かもしれないが・・・):MLP(多層パーセプトロン)は、ReLU などの従来の活性化関数を使用した場合、指数関数と正弦関数を効率的に近似することが困難な場合がよくある。対照的に、KAN は指数関数と正弦関数を効率的に近似できる。正弦関数と余弦関数は電力システム・ダイナミクス・モデルの基本関数であるため、KAN は MLP よりも電力システムのダイナミクスをより効果的に表現できる可能性がある。
(2) なお、本論文は、次のような「制限」にも言及している。
① 解釈可能性に関連して・・・PIKANモデルは、グリッド・ダイナミクスを正確に予測している。一方で、十分に学習された PIKAN によって提供される記号式は、ダイナミクスを正確に捉えていない。
本論文では、この矛盾の原因について、「現バージョンの KAN パッケージで利用できる記号式のライブラリが限られていることに起因している可能性がある。または、グリッド・ダイナミクスの式が、本質的に記号的ではない可能性がある」と説明している。
② 破滅的忘却について・・・安定したシナリオのデータで最初に学習された、十分に学習されたPIKANは、不安定なシナリオのダイナミクスでさらに学習すると、以前に学習したダイナミクスを忘れる傾向がある。
(3) 支配方程式の変数を、電気角から電気角速度に変えた場合は、どうなるのだろうか。もちろん数理的には変化しないはず。PINN-ⅠやPIKAN-Ⅰと同じ精度になるのだろうか。
また、単に、境界値を与える点の数を2倍に増やしたPINN-ⅠとPIKAN-Ⅰの精度は、PINN-ⅡとPIKAN-Ⅱの精度と、どの程度異なるのだろうか。
Do
中国ハルビン工業大学と豪ロイヤル・メルボルン工科大学の研究者は、「多頭注意(MHA🐾1)機構を備えたPIKANは、翼型周りの流れ場特性を高精度に予測できる」と主張する論文(以下、本論文[*20])を発表した(25年5月1日@Journal of Computational Physics)。言わずもがな、PIKAN=MLP(多層パーセプトロン)をKAN(コルモゴロフ・アーノルド・ネットワーク)に変えたPINNsである。
翼型(airfoil)とは”翼の断面形状”のことであり、ここで言う翼は、風力発電機の風車ブレードを指している。翼型は、ブレードの空力性能を決めるので、翼型周りの流れ場特性の理解は、ブレード設計において重要である。ここで言う流れ場の特性とは、速度分布、圧力分布、圧力係数、空力係数(=揚力係数、抗力係数、モーメント係数)を指している。
本論文のモデルが、”より良く予測できる”理由は、良く分からない(☞【6】)。
🐾1 Multi Head Attention
【1】本論文の主張
本論文は、翼型周りの流れ場特性予測において、以下を主張する:
(1) KAN+MHAは、学習損失・テスト損失、収束速度及び安定性の観点から、他モデル(☞【4】(1)0⃣)よりも優れている(☞【4】(1))。
(2) KAN+MHAは、他モデルよりも汎化性能に優れている(☞【4】(2))。
(3) KAN+MHAは、仰角に対する翼の性能を正確にシミュレートしている(☞【4】(2)4⃣)。
(4) KAN+MHAにおけるMHA機構は、「非線形性が強い領域に多くの注意を払うことで、強い非線形性下での予測値の精度を高める」(☞【5】)。
【2】為参考
[*21](25年6月24日@arXiv)は、PINNsの収束と学習効率を主要な焦点として、空力と流体力学におけるPINNsの最近の進歩を整理している。以下、簡単にまとめる。
(1) 適応型損失重み、学習率スケジューリング、活性化関数チューニングなどの手法は、収束を大幅に高速化する。
(2) 無次元化と、異なる学習タスクに重み付けするための定分散不確実性の利用により、PINN のパフォーマンスが大幅に向上する。
(3) 保守型PINNs(cPINN)は解が保存則に従うことを保証する。拡張型PINNs(XPINN)は、各部分ドメインにカスタマイズ可能なニューラルネットワークを用いることで、効率的な学習と堅牢な解の提供を可能にする。
(4) 影響関数の適用は、PINNsの解釈可能性と信頼性を高める。
(5) 物理法則と拡散モデルを組み合わせた、PiFusion(Physics-informed difFusionモデル)と呼ばれる物理学に基づく深層学習手法がある。モデルは、㊀プロセス+㊁プロセスで構成される:㊀流体力学シミュレーションにガウス・ノイズを追加する拡散プロセス。㊁物理学に基づくスコア関数に基づいて、速度場と圧力場を再構築するプロセス。
【3】本論文における技術的差異
(1) マルチソース・データ
0⃣ 概要
本論文はモデル学習に、「風洞実験データ、XFOILデータ、および数値流体力学(CFD)データ」で構成されるマルチソース・データセットを使用する。風洞データは、高精度の流れ場の測定を提供する。XFOIL🐾2は「小さな仰角と低レイノルズ数」という場合の分析に適している。CFD(シミュレーションの出力)データは、高レイノルズ数流れを学習するために準備されるから、CFDシミュレーションには、乱流解析用のモデルが使用される。
マルチソース・データを学習データとして使用する事で、モデルの予測精度が向上するだけでなく、複雑な流れの特徴を捕捉する能力も向上する(と、本論文は主張する)。
🐾2 下記1⃣㈡を参照。
1⃣ 補足
㈠ 風洞実験データ・・・ 本論文で使用した風洞実験データは、米国立再生可能エネルギー研究所とオハイオ州立大学が共同で実施した風洞試験プロジェクトから得られた、公開データセットである。翼型周りの流れ場に関する情報は提供せず、翼表面からの圧力係数データのみを提供する。データ数は、1520。
㈡ XFOIL・・・ XFOIL は、亜音速域における単独翼型の設計及び解析フリーソフト(GNU GPLライセンスの下で公開)。MITの教授が開発した。元のコードはフォートランで開発されたが、Python版も存在する。なお、XFOILデータのデータ数は、10,072。
XFOILは、主にパネル法と境界層理論に基づいている。パネル方法を使用して翼面を離散化し、噴出しと渦を分散することにより非圧縮性の流れをシミュレートする。粘性効果を説明するために、境界層理論を使用して、付着した境界層を修正し、流れの剥離と再付着を考慮する。
XFOILは、小さな仰角と低レイノルズ数で高精度を達成するが、その精度は高レイノルズ数と大きな仰角で減少する。これは、高レイノルズ数における乱流効果と、大きな迎角における複雑な流れの剥離を、XFOILモデルで正確に捉えることが困難であるためである。
㈢ CFD(乱流モデル)・・・ 乱流解析用のモデルには、レイノルズ平均モデル(Reynolds Averaged Navier-Stokes: RANS)が使用されている。レイノルズ応力の近似に用いられる乱流モデルは、k-εモデルである。なお、CFDデータのデータ数は、3,792。
2⃣ データの統合
マルチソース・データの統合は、①クラス/形状関数変換(Class/Shape Transformation:CST)法を用いた翼型のパラメータ化、②派生翼型の作成。を通じて行われた。様々な仰角およびレイノルズ数の下で、下記②で生成された様々な派生翼型を計算することにより、合計15,384のデータ・サンプルが生成された(およそ12,000が学習データセットに、およそ3,000がテスト・データセットとして使用された)。
① パラメーター化により、翼型の複雑な形状を、いくつかのパラメーターのみを使用して完全に説明することができる。これにより、ニューラルネットワークの複雑さを軽減し、派生翼型の生成を促進するのに役立つ。 CST法は、主にバーンスタイン多項式を使用して、翼型上部と下部を表現する。
本論文では、5次CST法がパラメーター化に使用される。この方法では、翼型の複雑な形状は、14個(上部6個+下部6個+後縁の厚さに2個)のCSTパラメーターのみを使用して表現できる。5次のCSTメソッドの最大絶対誤差は、4.23×10–4であり、翼型設計における5×10–4の許容要件を満たしている。
② イリノイ大学Urbana-Champaign(UIUC)翼型データセットには、約1,600の翼型のみが含まれている。深層学習方法では、多数のラベル付きサンプルが必要であり、UIUCデータセットだけではこの需要を満たすことができない。この制限に対処するために、データセットを拡張する。具体的には、ラテン超立方体サンプリング(LHS)メソッドを使用して、新しいCSTパラメーターをサンプリングし、派生翼型を生成する。
新たに生成された翼型が信頼性の高い空力性能と許容可能な幾何学的形状の両方を備えることを保証するために、特定の制約条件式🐾3を適用する。さらに、生成された翼型の厚さと輪郭の変化は、派生翼型形状の連続性と妥当性を維持するために、元の設計と一定レベルの整合性を維持しなければならない。上記プロセスを通じて、合計8,000セットの翼型を取得した。
🐾3 具体的な式は、本論文を参照(9頁の式(31)を参照)。本稿では、割愛。
(2) KAN+MHA
本論文では、単にKANと記述されているが、正確にはPIKANである。しかし、本稿でもPIKANとは書かずに、単にKANと表記する。KANの基底関数は、オリジナル通り、B スプライン関数である。KAN+MHAの入力は「2次元位置座標(つまり、xとy)🐾4、レイノルズ数、仰角、CST🐾5パラメータ」である。出力は、「x方向の流速ux及びy方向の流速uy、圧力p」🐾6である。空力係数と圧力係数は、流速と圧力から算出される。
ネットワークはマルチタスク学習アプローチを採用し、3 つの異なる予測ターゲット(出力)が個別に処理される。3つの出力(すなわち流速×2+圧力)のそれぞれに対して、アテンション・ヘッドが計算を実行する(ので、多頭注意となる)。
為参考:学習は、2つのNvidia Tesla 40GB A100 PCIE GPUを使用して、深圳のハルビン工科大学の施設で実施された。
🐾4 ちなみに、代表長さで無次元化されている。
🐾5 上記(1)2⃣①を参照。
🐾6 ちなみに、代表値で無次元化されている。代表速度は、自由流れの流速(自由流速)。代表圧力は、自由流れの静圧。
(3) 損失関数
流れのダイナミクスの支配方程式は、連続の式とナヴィエ・ストークス方程式であるから、それぞれの損失関数が計算される。境界損失・初期損失に加え、本論文では、風洞実験データを使った損失関数も考慮している。
ローカル重みは、”適応型重みを使う”などという、高級なことはしていない。驚くべきことに、全ての損失関数で同じ固定値を使う、という雑な扱いをしている。なお固定値とは、バッチ・サイズを使用している。また、グローバル重みについての記述はないが、単純に足しているのだろうか。MHAのお陰で、グルーバル重み・ローカル重みともに、雑な扱いをしても、高い精度が出るということなら素晴らしいが、やや腑に落ちない(☞【6】)。
【4】他モデルとの比較結果及び、KAN+MHAの汎化性能評価
(1) 比較結果
0⃣ 比較対象モデル等
❶MLP(実際は、PINNs)、❷MLP+MHA(つまりMHA付きのPINNs)、❸KAN(実際は、PIKAN)を⓪KAN+MHAと比較した。以下は、すべてのモデルで共通である:オプティマイザはL-BFGS。学習率初期値は0.20。学習率スケジューラは、StepLR🐾7を使用。バッチサイズは、236,000。学習エポック数は2000。
🐾7 一定のエポック数ごとに、学習率を定数倍減衰させるスケジューラ。
出所:https://docs.pytorch.org/docs/stable/generated/torch.optim.lr_scheduler.StepLR.html
1⃣ 学習損失の定量的・定性的比較、及びテスト損失の定量的比較
最終的な学習損失(以下、単に学習損失とする)の定量的な比較は以下の通りである:⓪KAN+MHAの最終的な学習損失は2.0×10–3である。本論文で示されている、KAN+MHAの学習損失に対する他モデルの学習損失の比率を使って、他モデルの学習損失を計算すると🐾8、❶9.52×10–2、❷3.92×10–2、❸5.49×10–3である。つまり、⓪KAN+MHAが優れている。
テスト損失は、x方向の流速uxについては、❶2.1×10–2、❷1.1×10–2、❸7.1×10–3、⓪2.5×10–3である。流速uyについては、❶1.6×10–2、❷1.2×10–2、❸9.5×10–3、⓪3.0×10–3である。圧力については、❶3.1×10–2、❷9.8×10–3、❸4.3×10–3、⓪1.4×10–3である。全てにおいて、⓪KAN+MHAが優れている。
定性的な比較は、以下の通り。総論としては、「KAN+MHAモデルは、最終的な学習損失、収束速度、および安定性の観点から、他3モデルよりも優れている」旨が述べられている。各論としては、次のように述べられている(が、議論がやや強引に思える):エポック数に対する学習損失の推移において、MLPやMLP+MHAは、顕著な振動🐾9及び収束が遅い🐾10ことを示している。対照的に、KAN+MHAは、最初の数百エポック内で急速に安定する。これは、データの分布を効率的に学習し、過学習を回避できることを示している🐾11。
メカニズム的には、次のように説明されている:KAN+MHAは、KANに多頭注意機構を組み込むことで、最も関連性の高い特徴量に選択的に注意を払うことができる。そのおかげで、ノイズが減り、最小限の変動で安定した状態に到達し、安定性と収束が強化される。
「最も関連性の高い特徴量に選択的に注意を払うことができる」を流体力学の文脈で解釈すると、「複雑な流れ場パターンを、効率的に捕捉することができる」ことを意味する(だろう)。
🐾8 ちなみに、MLP+MHAとKANに関しては、本論文中においても最終的な学習損失の値が示されている。具体的には、MLP+MHA→3.9×10–2、KAN→5.5×10–3である。
🐾9 KANやKAN+MHAに比べて、顕著な振動があるようには見えない。
🐾10 MLPの収束は、確かに遅いかもしれない。しかし、MLP+MHAは、KANやKAN+MHAに比べて、”全体的な傾向”として、収束が遅いようには見えない。ただし、初期(最初の数百エポック)における収束の速さ(下降の急峻さ)という意味であれば、確かに、劣っているかもしれない。
🐾11 初期(最初の数百エポック)における挙動は、KANとKAN+MHAで同じに見える。すると、KANも「データの分布を効率的に学習し、過学習を回避できる」ことになるだろうか。
2⃣ 勾配ノルムの時間発展
本論文は、勾配ノルムの時間発展を評価軸にして、KAN+MHAの収束の安定性と速さについて、以下のように分析している。
MLPとMLP+MHAは学習プロセス全体で比較的高い勾配ノルムを維持する一方、KANとKAN+MHAは低勾配ノルムを示す。これは、MLPが最適化のためにより大きな勾配更新に依存しているのに対し、KANは勾配の変動が少ない、より安定した最適化軌道に従うことを示している。特に、学習初期段階では、KANとKAN+MHAは、MLPよりも著しく高い勾配ノルムを持っている。さらに、高い勾配ノルムは、最初の10エポック内で急速に減少する。これは、KANモデルが最初により急な最適化パスに従い、迅速なパラメーターの調整とより速い損失削減を可能にすることを示唆している。学習が進むにつれて、KANとKAN+MHAの勾配ノルムはすぐに低下して安定するが、MLPは比較的高い勾配ノルムを維持し、その最適化プロセスが一貫した大きな勾配更新に依存することを示している。
3⃣ 流速及び圧力の定性的な比較
予測値とグランドトルゥースとの差を指標として定性的にモデル間比較を行っているが、割愛。結論は、KAN+MHAのパフォーマンスが優れている。
4⃣ 流れ場の予測についての比較
具体的なケースを使って、モデル間の”俯瞰的な”比較を行っている。具体的なケースとは、「Re = 1×105及び仰角 = 0°の条件で、AG19翼型🐾12」の流れ場の予測、である。なお、流速、圧力共に、無次元化していることに注意(☞🐾6)。もちろん、結論は、KAN+MHAが優れている、である。
x方向の流速uxにおける予測値とグランドトルゥースとの絶対値でとった差異の最大値(最大絶対誤差)は、❶1.8×10–1、❷5.8×10–2、❸3.5×10–2、⓪9.7×10–3である🐾13。
y方向の流速uyは、❶1.2×10–1、❷4.1×10–2、❸6.9×10–2、⓪1.8×10–2である。つまり、❷が❸よりも小さい。
圧力pは、❶1.2×10–1、❷7.2×10–2、❸3.4×10–2、⓪9.8×10–3である。
🐾12 イリノイ大学Urbana-Champaign(UIUC)翼型データセットに含まれている翼型。形状はhttps://m-selig.ae.illinois.edu/ads/afplots/ag19.gifを参照。
🐾13 ❶、❷、❸、⓪の意味は、0⃣を参照。
(2) KAN+MHAの汎化性能評価
1⃣ 流速
ここでは、流速=√ux2+uy2、を使用する。ザックリと結論を述べると、KAN+MHAは、さまざまなデータセット(つまり、XFOILデータとCFDデータの双方における、様々な条件下)で、高い予測精度を示している。 汎化性能が高い、という評価で良いだろう。
様々な条件下とは、異なる翼型、広いレイノルズ数(Re)範囲、広い仰角範囲を意味している。正確に述べると、XFOIL、CFDそれぞれで3つの翼型を採用している🐾14。Reは、XFOILが1~10×104であり、CFDが1~505である。仰角は、XFOILが-5~10°で、CFDが-10~25°である。
細かく言えば、XFOILデータは仰角が大きくなると、誤差が大きくなる🐾15。本論文では分析されていないが、Reに関しては、明確な傾向は見られない(と思われる)。CFDデータは、Re、仰角ともに、明確な傾向は見られないと思われる。翼型の違いによる影響が最も大きい。
🐾14 具体的には、XFOILについて、NACA0021、NACA2415、SD7032。CFDについて、DU20、DU40、NACA64-618。NACA翼型は、アメリカ航空諮問委員会(NACA、NASAの前身)が開発した翼型の総称。SDは、UIUC翼型データセットに含まれている翼型。DUは蘭デルフト工科大学によって開発された翼型。
🐾15 ただし、翼型による。
2⃣ 圧力
分析”結果”は、本質的に流速のケースと同じなので、割愛。
3⃣ 圧力係数及
Re = 1 × 106、仰角 = 0°におけるSD7032翼型の流れ場を予測し、翼型の上面および下面の圧力係数を算出した。KAN+MHAによって予測された圧力係数曲線が、グランドトルゥース(=数値シミュレーションから得られた圧力係数曲線)の良い近似になっていることから、本論文では、KAN+MHAは翼型周りの流れ場情報を効果的に捉えている、と結論している。この傾向が、翼型の前縁(x < 0.2)及び後縁(x > 0.8)において特に顕著であるこ、とが指摘されている。
前縁及び後縁は、境界層の剥離や再付着といった複雑な現象のために、予測が困難な場合が多い。それにもかかわらず、最大絶対誤差はわずか9.8 × 10–3であるため、KAN+MHAの性能は優れている、と結論されている。
4⃣ 空力係数
圧力係数と同じ「Re = 1 × 106、仰角 = 0°におけるSD7032翼型」というセットアップで、空力係数を算出した。揚力係数(CL)、抗力係数(CD)、およびモーメント係数(CM)の予測曲線は、グランドトルゥース(=数値シミュレーションから得られた予測曲線)と良く一致している。定量的に言うと、3つの係数における絶対誤差は、CL:2.71×10–2、CD:2.93×10–2、およびCM:2.68×10–2である。
定性的に言うとKAN+MHAは、仰角増加→ストール(失速)発生→CL上昇→CL急低下、という傾向を良く捉えられている。つまりKAN+MHAは、仰角に対する翼の性能を正確にシミュレートしており、ストールの臨界発生点を効果的に捕捉できることを示している。
【5】注意機構の有効性評価
1⃣ 総論
MHAの有効性を評価するために本論文では、「Re = 1 × 105、仰角0°および-10°及び AG19 翼型」というセットアップに対して、翼型周り流れ場の「注意重み」を計算している。
uxに対する注意重みは、KAN+MHAが『翼型上の高速領域と翼型周囲の気流変化に、より注意を払っている』ことを示している。uyに対する注意重みは、KAN+MHAが『翼型下面と後縁に、より注意を払っている』ことを示している。圧力に対する注意重みは、KAN+MHAが『前縁の高圧領域と後縁の低圧領域に、より注意を払っている』ことを示している。これらは、流体力学的ドメイン知識と一致するので、MHAは、翼型周り流れ場の特徴を適確に捕捉していると考えられる。
2⃣ 個別論
さらに本論文は、 翼型流れ場が大きな変化を遂げる仰角−10°の場合について、議論している。uxは、-10°の場合、翼端で顕著な高速領域が現れる。uyは、-10°の場合、翼型下端に大きな下向きの流れが現れる。圧力は、-10°の場合、前縁に顕著な負圧領域が流現れる。
MHA(多頭注意)機構は、これらの流れ場の変化を効果的に捕捉している。ux及びuyで注意機構は、前縁と後縁など、大幅な流れ場の変化を伴う領域に、大きな注意重みを割り当てている。さらに、仰角0°と比較して、注意重みが大きい領域が増えており、この注意重み分布の変化は、流れ場の実際の変化に対応している。特に、圧力予測では、注意機構は負圧領域の重みを大幅に増加させている。
本論文は、上記の結果について、以下のようにまとめている:多頭注意機構が、より複雑な流れ場の変動を備えた領域に焦点を合わせてネットワークを効果的に導き、それにより、高度に非線形な領域における予測精度を高めることを示している。
【6】考察
(0) ちなみに、本論文では【2】で整理した手法は、(少なくとも陽的には)使われていない。
(1) 本論文の手法(KAN+MHA)が高い性能を示した理由の一つは、学習にマルチソース・データを使ったことであろうか。これは、レイノルズ数に対して、一種のカリキュラム学習になっていると考えられる。ただし、マルチソース・データの使用は、他3つのモデルに対しても同様である。
(2) KAN+MHAは、マルチタスク学習を採用している。そして、マルチタスク学習とマルチヘッド注意機構が対応している。マルチタスク学習は、収束の加速や精度向上に貢献しているであろうか。[*22]には、「マルチタスク学習は、KANの汎化性能を向上させる可能性がある」旨の記述がある。従って、汎化性能の向上に貢献しているのかもしれない。
(3) MHAが、翼型周りの流れ場の特性を正確に捕捉していることは、間違いないのだろう(☞【5】)。MHAの採用が結果的に、ローカル重みを「実質的な意味」で、適応型にしているという解釈が可能であろうか。ただ、MHAが大きく効いているというのなら、MLP+MHAがKANより精度が低いという結果は、腑に落ちない・・・MLP+MHAがKAN単体よりも精度が高いのなら、肚落ちしただろう。つまり、KAN+MHAが他モデルよりoutperformする理由は、良く分からない(ように思われる)。
(4) 良く分からない、という結論に達したところで、次のように考えれば、全て得心がいく:KANが「翼型周りの流れ場予測」に上手くハマった。本論文のケースでは、(KAN+MHAではなく)KANがMLPよりも適していたと盲目的に🐾16、と考えれば諸々のモヤモヤは解消する。MHAはブースターであり、MLPもKANのどちらに対しても、性能アップに貢献すると整理すれば良い。
🐾16 盲目的という表現は、ややキツイかもしれない。教科書的には(=雑に言うと)、「KANはMLPよりも、偏微分方程式を解くのに適している」。つまり、流れ場を高精度に予測しても、何ら矛盾は生じない。
(5) 本論文では(PINNs、PIKANともに)、損失関数のグローバル重み及びローカル重みは”雑に”扱われている。正則化も行われていない。MHAが結果として、自動的に適応型の重み付けを実行しているのであれば、MHAはブースター以上の役割を果たしていると言えるだろう。
❚為参考❚
[*23]では、NACA0012翼型周りの遷音速流れにPINNsやPIKANを適用したケースが示されている。驚くべきことに、PDE損失のグローバル重みは、2×104と設定されている。そんな値に意味があるのだろうか? 境界損失のグローバル重みは、1である。
【尾注】
*1 Ziming Liu et al.、KAN: Kolmogorov–Arnold Networks、https://arxiv.org/pdf/2404.19756
ちなみに、上記はver4に該当する。末尾にv1をつける(つまり、https://arxiv.org/pdf/2404.19756v1とする)とver1を表示させることができる。ver2,ver3でも同様。
*2 https://www.quantamagazine.org/novel-architecture-makes-neural-networks-more-understandable-20240911/
*3 Ziming Liu et al.、KAN 2.0: Kolmogorov-Arnold Networks Meet Science、https://arxiv.org/pdf/2408.10205
*4 新美潤一郎、Kolmogorov–Arnold Network のマーケティング解析への応用可能性の検討、https://jxiv.jst.go.jp/index.php/jxiv/preprint/view/893
*5 Runpeng Yu et al.、KAN or MLP: A Fairer Comparison、https://arxiv.org/pdf/2407.16674
*6 中西賢次、2019年度(第41回)数学入門公開講座テキスト(京都大学数理解析研究所,2019年7月29日~8月1日開催)|関数不等式とエネルギー集約、https://www.kurims.kyoto-u.ac.jp/~kenkyubu/kokai-koza/R1-nakanishi.pdf
*7 Yizheng Wang et al.、Kolmogorov–Arnold-Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov–Arnold Networks、https://arxiv.org/pdf/2406.11045
*8 Alex Davies et al.、Advancing mathematics by guiding human intuition with AI、https://www.nature.com/articles/s41586-021-04086-x
*9 合田洋、第64回トポロジーシンポジウム|結び目の体積とアレキサンダー多項式、https://www.mathsoc.jp/section/topology/topsymp/2017/ts2017Goda.pdf
*10 Alex Davies et al.、THE SIGNATURE AND CUSP GEOMETRY OF HYPERBOLIC KNOTS、https://arxiv.org/pdf/2111.15323
*11 岡田幸平・橋口徳一、絡み目理論の符号数と退化次数、https://www.cst.nihon-u.ac.jp/research/gakujutu/56/pdf/P-4.pdf
*12 Akash Kundu、KANQAS: Kolmogorov-Arnold Network for Quantum Architecture Search、https://arxiv.org/pdf/2406.17630
*13 Khemraj Shukla et al.、A comprehensive and FAIR comparison between MLP and KAN
representations for differential equations and operator networks、https://arxiv.org/pdf/2406.02917
*14 Sokratis J. Anagnostopoulos et al.、Residual-based attention and connection to information bottleneck theory in PINNs、https://arxiv.org/pdf/2307.00379
*15 Yichuan HE et al.、An artificial viscosity augmented physics-informed neural network
for incompressible flow、https://link.springer.com/article/10.1007/s10483-023-2993-9
*16 JEAN-LUC GUERMOND et al.、ENTROPY VISCOSITY METHOD FOR NONLINEAR CONSERVATION LAWS、https://people.tamu.edu/~guermond//PUBLICATIONS/MS/non_stationnary_jlg_rp_bp.pdf
*17 Raissi M, Perdikaris P, Karniadakis GE、Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations、https://www.sciencedirect.com/science/article/pii/S0021999118307125
*18 Hang Shuai & Fangxing Li、Physics-Informed Kolmogorov-Arnold Networks for Power System Dynamics、https://arxiv.org/pdf/2408.06650
*19 北内義弘、解説|電力系統の安定運用のために 再生可能エネルギー大量導入時の基幹系統への影響、日本原子力学会誌,Vol.61,No.7 (2019)、pp.535-539、https://www.jstage.jst.go.jp/article/jaesjb/61/7/61_535/_pdf
*20 Siyao Yang et al.、The KAN-MHA model: A novel physical knowledge based multi-source data-driven adaptive method for airfoil flow field prediction、https://www.sciencedirect.com/science/article/pii/S0021999125001299
*21 Afila Ajithkumar Sophiya et al.、PHYSICS-INFORMED NEURAL NETWORKS FOR INDUSTRIAL GAS TURBINES: RECENT TRENDS, ADVANCEMENTS AND CHALLENGES、https://arxiv.org/pdf/2506.19503
*22 SHRIYANK SOMVANSHI et al.、A Survey on Kolmogorov-Arnold Network、https://arxiv.org/pdf/2411.06078
*23 Guoqiang Lei et al.、Discontinuity-aware KAN-based physics-informed neural networks、https://arxiv.org/pdf/2507.08338

