そこ曲がったら、量子坂？(上り) Appendix

【0】はじめに
　インド工科大学マドラス校と印ITサービス企業タタ･コンサルタンシー･サービシズは、DNN-VQEアプローチについて、幅広く検討した論文[*A-8](以下、本論文)を発表した(23年12月4日)。DNN-VQEアプローチとは、計算精度(予測精度)を上げるために、VQE^†1を深層学習(DNN)で支援したアプローチである(詳細は後述)。
　本論文では、NISQデバイス^†2を含めて、DNN-VQEアプローチの評価が行われている。｢NISQデバイスを使用して実行されるVQE の結果は、ノイズのない状態ベクトル･シミュレータや、古典コンピュータで得られた結果から大きく乖離することがよくある｣ため、実機であるNISQデバイスを含めている。
†1　Variational Quantum Eigensolver：変分量子固有ソルバー法。ただし、和訳は数種類存在する。また、VQA(Variational Quantum Algorithm)と言ってもほぼ同じ意味。
†2　Noisy Intermediate-Scale Quantumデバイス。量子誤り訂正が施されていない｢量子コンピュータ｣。誤り訂正の代わりに、誤り軽減が適用される。

【1】本論文から導かれる結論　
(1)　DNN-VQEアプローチは、VQEアプローチよりも、高い精度で予測できる。
(2)　誤り緩和策を使っても、NISQデバイスで予測できるのは、H₂分子まで。

【2】事前整理
(1)　DNN-VQE
　分子の結合距離とパラメータθで構成されるデータセットで、学習された深層ニューラルネットワーク(DNN)の出力θを、初期パラメータとして使用するVQEを、DNN-VQEという。ここで、θは特定の結合距離における分子の基底状態エネルギーを与えるパラメータである。本論文で扱う分子は、 H₂及びLiHであるから、｛H-H及びLi-Hの結合距離、θ｝がデータセットとなる。学習済モデルは、学習データにはない結合距離における最適なパラメータを予測できる。
　本論文では、 2 つの異なるDNN-VQE、DNN1とDNNFを用いている。DNN１は、VQEで最適化されたパラメータと学習済DNNの出力を同一視する。つまり、学習済DNNが予測したパラメータθをそのまま使って、基底エネルギーを計算する(VQEは実行しないため、厳密に言えば、DNN-VQEという表現はおかしい)。DNNFは、学習済DNNが予測したパラメータθを初期パラメータとしてVQEを行なう、いわゆる普通のDNN-VQEである。通常のVQEは、ランダムな値を初期パラメータとして使用する。

(2)　結合クラスター法
　電子に対する平均場近似であるハートリー･フォック(HF)近似に、電子相関(HF波動関数と厳密な波動関数との差)を取り込む手法には、配置間相互作用法(CI法)、摂動法、結合クラスター法(Coupled Cluster：CC法)などがある。本論文では、CC法が取り上げられている。
　CC法は、HF基底配置から、励起配置を作る励起演算子を導入することで、電子相関を取り込むという戦略を採用する。CCD(Coupled Cluster Double.他にもあるが省略。以下、同。また、日本語では、2電子励起結合クラスターと呼ばれる)というCC法は、2励起演算子のみを、考慮する。CCSD( Coupled Cluster Single and Double)は、1励起演算子及び2励起演算子を考慮する。CCSD(T)は、 Coupled Cluster Singles, doubles and perturbative Triplesの略であり、CCSD計算の結果に、3電子励起の効果を、摂動的に加える。Tに付いている()は、一般的に用いられる()よりも、ちゃんとした意味を持っている。分かり辛いが、Tに付いている()は、｢3電子励起の効果は、摂動的に取り込んだ｣ことを意味している。故に、CCSDTも存在するし、CCSD[T]というCC法もある(が、説明省略)。
　精度はCCSD(T)が最も高いが、計算コストも高い。精度と計算コストのバランスを取ることは重要であり、CC法では、CCSD(T)が代表的手法(Gold Standard)と呼ばれている。本論文では、CCSD法が採用されている。

(3)　アンザッツ及び、鈴木･トロッター分解
　VQEでは、アンザッツとよばれるパラメータ付き量子回路を導入し、古典的にパラメータを最適化することで、計算対象の基底エネルギーを求める。アンザッツは、参照波動関数と呼ばれる初期状態にユニタリー演算子を作用させることで構成することができる。CCSD法を採用した場合のアンザッツ、つまり 1励起演算子及び2励起演算子を考慮する場合のアンザッツは、2つの励起演算子を考慮したユニタリーCCSD演算子(UCCSD演算子)を参照波動関数に作用させることで構成できる。
　NISQデバイスも誤り耐性量子コンピュータも、ゲート形式量子コンピュータであるが、ゲート形式の量子コンピュータは、通常、1量子ゲートと2量子ゲートで構成される。従って、ゲート形式量子コンピュータを使用する場合、UCCSD演算子も1量子ゲートと2量子ゲートに分解する必要がある。この分解は、鈴木･トロッター近似を使用して実行される。鈴木･トロッター近似では、演算子の指数和が指数演算子の積に分解される。UCCSD 演算子を正確に分解するには、多数の近似次数(ステップ) が必要である。多数のステップは、量子回路の深さを、深くする。
　本論文には、以下の先行研究を引用している：小分子であれば、トロッター･ステップが1回であっても、基底状態エネルギーが正確に計算できる。本論文て扱う分子は、H₂ やLiHのように小分子であるため、トロッター･ステップは1回を採用している。

(4)　ジョルダン･ウィグナー(Jordan-Wigner)変換
　反対称性を考慮した多体量子系(多粒子系)の計算を、系統的かつ効率的に行うためには、第2量子化の手法は便利である。つまり、多電子系の電子状態を求める量子化学では、第2量子化の手法が有効である。ただし、第2量子化の基本要素である｢消滅演算子及び、生成演算子｣は、量子コンピューターで使用される量子ビット演算子(パウリ演算子)と、直接的に＝何らかの｢変換｣を施すことなく、置き換えることはできない。消滅演算子及び、生成演算子をパウリ演算子に｢変換｣する手法は、ブラヴィ･キタエフ変換とジョルダン･ウィグナー変換等が存在するが、本論文では、最も単純と言われるジョルダン･ウィグナー変換を選択している。
　なお、ブラヴィ･キタエフ変換を使ったほうが、ハードウェア効率が高いことが知られている。つまり、量子ビット数やゲート数が少なくて済む。ただし、本論文では、ジョルダン･ウィグナー変換後に、パリティ･マッピングとZ₂対称性を使用して、量子ビット数を減らしている。ちなみに、これらの変換を自動で行ってくれるPythonライブラリ(OpenFermion[例えば、*A-9])がある。

(5)　Twirled Readout Error eXtinction(T-REX)誤り緩和策
　誤差を軽減した平均値を推定するために、測定回路と校正回路を追加することによって、測定ノイズを低減する、一般的かつ効果的な手法である[*A-10]。IBM発の量子コンピュータ用SDKであるQiskitに実装されている。
　測定直前にXゲートを介して量子ビットをランダムに反転させ、Xゲートが適用された場合は対応する測定ビットを反転させることにより、測定に関連するノイズチャネルを対角化することで測定誤差を低減する。対角化されたノイズ・チャネルからのリスケーリング項は、ゼロ状態で初期化されたランダム回路のベンチマークによって学習される。これにより、読み出しノイズに起因する期待値のバイアスを除去することができる[*A-11]。

【3】DNN-VQEの検証結果　
(0)　セットアップ
1⃣　計算環境　
❶　状態ベクトル量子シミュレータ　⇒　ibmq_qasm_simulator
❷　NISQデバイス　⇒　 ibm_brisbane(127量子ビット)
2⃣　ニューラルネットワーク環境　
❶　VQEのオプティマイザー　→　L-BFGS_B(Broyden-Fletcher-Goldfarb-Shannon Bound)　
❷　DNNのオプティマイザー　→　Adam　
❸　DNNの活性化関数　→　ReLU　
❹　コスト関数　→　平均絶対パーセント誤差(MAPE)　
❺　基底関数　→　STO-3G　
❻　ショット数(量子回路の測定回数)　→　4,000　

(1)　検証の概要
　 グランドトルゥース(正解)は、古典コンピュータ上でCCSD法使い計算した結果である。評価指標は、基底エネルギー(の差)である。比較対象は、シミュレータ(ノイズなし、ノイズあり)とNISQデバイスを使って、実行されたVQE、DNN1、DNNFの結果である。H₂は、結合距離0～3Åにわたり計算した。量子回路として、1量子ビット量子回路(深さ1)を選択している。LiHは、0.7～3.7Åにわたって計算した。量子回路は、6量子ビット量子回路(深さ482)である。
　VQEは、UCCSDアンザッツを使用している。シミュレータに取り込んだノイズは、NISQデバイスibm_brisbane のデバイス･ノイズである(今は、そういうことが、出来るようになっている[らしい])。

(2)　検証結果の詳細
1⃣　ノイズがない状態ベクトルシミュレータでの結果
❶　H₂分子
　DNN1による基底状態エネルギーの予測値とグランドトルゥースとの差(偏差)は、結合距離に対して変動するが、変動幅は、1 × 10^–7から 1 × 10^–5ハートリーの範囲に収まっている。結合距離が伸びるにつれて、差は、横這い～やや減少傾向にある。DNNFの偏差は、VQEの偏差と区別がつかない程、同じである。結合距離に対して変動するが、変動幅は、1 × 10^–10から 1 × 10^–7ハートリーの範囲に収まっている。結合距離が伸びるにつれて、差は、減少傾向にある。
　3者の比較は、VQE≒DNNF＞DNN1、である(VQEとDNNFの予測精度は同程度。DNNFは、DNN1より予測精度が高い)。ただ、VQE/DNNF/DNN1の全てで、偏差は許容できる。
❷　LiH分子
　DNN1の偏差は、変動幅は、1 × 10^–6から 1 × 10^–5ハートリーの範囲に収まっている。結合距離が伸びるにつれて、差は、減少傾向にある。DNNFの偏差と、VQEの偏差は、結合距離およそ3Å以上の範囲を除いて、同じである。変動幅は、1 × 10^–10から 1 × 10^–7ハートリーの範囲に収まっている。結合距離が伸びるにつれて、差は、減少傾向にある。
　比較は、VQE≒DNNF＞DNN1、であり、偏差は全て許容できる。
2⃣　ノイズがある状態ベクトルシミュレータでの結果
　ノイズがある状態ベクトルシミュレータでの結果は、NISQデバイスでの結果と一致することは、示されている。
❶　H₂分子
　DNN1と DNNFの偏差は、1 × 10^–4から 1 × 10^–2ハートリーだけズレている。VQEの偏差は、ほぼ1 × 10^–1ハートリーだけズレている。この結果は、結合距離に、ほぼ依存しない。
　なおDNN1とDNNFとを比較した場合、結合距離の全範囲において、DNNFの精度が高い。その傾向は、結合距離が短いと顕著である。結合距離が長くなると、差は、ほぼない。また結合距離が長くなると、DNN1の偏差は、やや縮小する傾向がみられる。一方、DNNFでは、やや増大する傾向がみられる。
　また、まとめ的に3者を比較すると、DNNF≒DNN1＞VQE、である。
❷　LiH分子
　DNN1、DNNF、VQEのいずれも、偏差は1.1～1.6ハートリーと大きくズレている。この差は、許容範囲を超えており、シミュレーション結果として使えない。細かくみることは、ほとんど意味がないが、結合距離が短い範囲ではDNNF≒VQE、長い範囲ではDNN1≒VQE、という傾向がみられる。
　本論文では、この原因は、量子ビット数の増加と、量子回路の深さが深くなったことにある(ことを実証している)。

[参　考]　計算時間
　T-REX誤り緩和策を用いた、ノイズありシミュレータでの計算時間を以下に示す[*A-12]。なお、結合距離によって計算時間が変わるので、値には幅がある。
1⃣　H₂分子
❶　VQE　→　15～34分　
❷　DNNF　→　14～32分　
❸　DNN1　→　およそ1分　
2⃣　LiH分子　
❶　VQE　→　3～8日　
❷　DNNF　→　3～6日　
❸　DNN1　→　23～26分　

【4】感想など・・・
(1)　本論文の趣旨は、DNN-VQEの検証。しかし、デバイス･ノイズが存在する実機である｢NISQデバイス｣での計算が、使い物にならないという衝撃が大き過ぎる。ノイズがありだと、水素分子以外は、使い物にならない。LiH分子では、量子誤り緩和策を適用しても、NISQデバイスは使えない。従って(ノイズがありで、水素分子の場合)、DNN-VQE＞VQEであるものの、そのインパクトは、ほぼない(イメージ)。
(2)　NISQデバイスでも有用ですよ！という趣旨の論文は、実際は、古典シミュレータの結果から判断している。実際どうなの？ということで、検証してみたら･･･案の定という結果。ノイズの影響を公平に比較するために、ノイズありシミュレータとノイズなしシミュレータで比較している。NISQデバイス＝ノイズありシミュレータは、担保されている(実機固有のデバイス･ノイズをシミュレータに反映できる)。
(3)　直ぐに浮かぶ試行策は、以下のようなものだろう：㊀CCSD(T)を使ったらどうか。㊁トロッター･ステップを増やしたらどうか。㊂ブラヴィ･キタエフ変換を使ったらどうか。㊃誤り緩和策として、ZNEやPEC等を適用したらどうか。
(4)　各種試行しても、NISQデバイスでは、水素分子以外はダメとなったら、誤り耐性量子コンピュータを待つしかない、という結論だろうか。

【0】はじめに
　ゲート方式の量子コンピュータで、忠実度＝1を満たす最小の量子回路規模を、事前に知っておくことは、非常に価値がある。いわゆる、量子リソース推定という作業である。量子リソース推定はスパコンを使った量子シミュレーションによって行われるが、推定できるのは、量子ビット数が小さい場合に、現状、限られている。
　情報通信研究機構他[*A-13]の研究者は、量子ビット数が大きい場合でも、｢忠実度=1の量子回路を探索する方法を構築｣し、その手法の｢有効性を実証した｣と主張する論文[*A-14](以下、本論文)を発表した(24年5月6日@arXiv)。

【1】本論文の主張
　本論文は、以下を主張する：
(1)　量子ビット数nを与えた場合に、 忠実度=1を達成する最小CNOTゲート数を推定することができた。推定の対象は、状態準備とトランスパイルである。
(2)　忠実度=1を達成するために必要な最小CNOTゲート数を超えると、忠実度=1の量子回路の割合が急速に増加する。

【2】事前整理
(1)　状態準備　
　量子コンピュータにおいて任意の操作を行う(演算を実行させる)には、量子状態を作成する必要がある。量子実験のデータをそのまま量子コンピュータの入力として使用するような場合を除けば、入力データは古典状態にある。従って量子演算を実行するには、なんらかの量子操作が必要となる。この操作を、(初期)状態準備と呼ぶ。
　なお、量子複製不可能原理が存在するため、量子演算の場合、演算する度に状態準備が必要となる。量子計算は、演算速度は速いと目されている一方で、演算(を繰り返す)回数は多い。従って、状態準備にかかる計算コストが過大であると(＝長い準備時間を要すると)、量子計算の魅力の一つとされる演算に要するトータル時間が、相対的に長くなってしまう。これが、いわゆるデータ･ローディング問題である。データ･ローディング問題のため、量子アルゴリズムは2次加速では不足で、指数加速が必要と考えられている。

(2)　トランスパイル　
　量子演算におけるコンパイルは、しばしばトランスパイルと呼ばれる。本論文では、ユニタリー演算子の合成と呼ばれている。トランスパイルは、ユニバーサルゲート･セットの中から、特定の量子演算を実行する、量子ゲート･シークエンスを構築する手続きである。量子ゲート･シークエンスの構築は、特定の量子演算を、ユニタリー演算子で分解･再構築することと等価である。(基本的な)量子ゲート･シークエンスは、しばしば量子回路と呼ばれる。
　ユニバーサルゲート･セットは、一意に定まらない。特定の量子演算を実行する量子ゲート･シークエンスも、一意ではない。最も少ない量子ゲート数で、特定の量子演算を実行する、量子ゲートの組み合わせを見つけることが、トランスパイルの目的である。本論文では、ユニバーサルゲート･セット^✒1として、{適当な1量子ビットゲート＋CNOTゲート}を選択している^✒2。CNOTゲートを選択した理由は、｢CNOTゲートは、超伝導方式量子デバイスにとって、自然な2量子ビットゲート｣であるため、とされている。
　なお、Bゲート^✒3及び、トフォリ･ゲートについての議論は、割愛する。
✒1　ユニバーサルゲート･セットが実装されていれば、任意の量子計算が可能である。
✒2　ソロヴェイ･キタエフの定理より、適当な1量子ビットゲート＋CNOTゲートは、ユニバーサルゲート･セットを構成する。
✒3　Bゲートは、次のように表される[*A-15]：exp(π/2･i/2･σ¹_xσ²_x)･exp(π/4･i/2･σ¹_yσ²_y)　ここで、σ¹_xσ²_xは、σ_xⓍσ_xを意味する(添え字yでも同じ意味)。σ_xは、パウリのx行列である。B ゲートを使用すると、CNOT ゲートよりも効率的に任意の 2 量子ビット ゲートを合成できることはよく知られている。しかし、B ゲートを実装する際の実験上の困難さは、B ゲートが提供する利点を上回る可能性がある、とも言われている。

(3)　忠実度　
　忠実度(fidelity)Fは、量子状態の類似度を表す指標である。状態準備の場合は、初期量子状態|0⟩にユニタリー演算子を作用させてた準備した量子状態と、ターゲット量子状態の類似度を表す。ターゲット状態は、機械学習の言葉を使えば、グランドトルゥースである。状態準備のFを式で表せば、
　　　F＝tr[ρ_FU(T)ρ₀U^†(T)]
となる。trはトレース。ρ₀は、初期密度演算子(すべての量子ビットが状態|0⟩)である。ρ_Fは、ターゲット量子状態を表す密度演算子である。U(T)は、量子回路によって生成されるユニタリー演算子(時間発展演算子)で、U^†(T)はU(T)のエルミート共役(一般にh.c.と略される)である。U(T)ρ₀U^†(T)は、初期密度演算子が時間発展した密度演算子を表すから、
　　　F＝tr[ρ_Fρ(T)]
と表すこともできる。こちらの方が、見た目上、ユニタリー演算子合成の場合と平仄が合うかもしれない。
　ユニタリー演算子合成の場合は、
　　　F＝|tr[U_F^†U(T)]/2ⁿ|²
で表される。U_Fは、ターゲットとなるユニタリー演算子である。
　なお、Fは、1 − F < 10⁻⁸で1とみなされる。10⁻⁸が選択された理由は、この値を下回る F = 1 からの偏差が数値誤差に起因すると考えられるほど十分に小さいためである。

(4)　先行研究による知見　
　 n 量子ビットを使って構成可能な全てのCNOT ゲートを考える。ユニタリー演算子の合成の場合、nが3から4に増加すると、ゲート構成の数は、約 10⁴¹倍増加する。このような超指数関数的な増加のため、｢忠実度＝1｣を達成するCNOT ゲートを、総当たり方式で探索することは不可能である。ちなみに状態準備でも、nが6から7に増加すると、約 10⁴⁵倍増加する。
　幸いなことに、構成可能なCNOTゲートの”わずか”20％を探索することで、忠実度＝１で量子演算を実行できるCNOTゲートを見つけられることがわかった。この発見の重要な帰結は、CNOTゲートをランダムにいくつか作成して忠実度を調べる、という確率的なアプローチでも、忠実度＝１を達成するCNOTゲートを見つけられるだろうという仮説である。☛本論文は、この仮説を検証している。

【3】本研究の結果　
(1)　最小CNOTゲート数N_minの推定　
　状態準備の場合、忠実度=1を達成する最小CNOTゲート数N_minは、⌈(2ⁿー1ーn)/2⌉と推定される。ここで、nは量子ビット数、⌈x⌉は、 x以上である最小の整数を表す。ユニタリー演算子合成の場合は、⌈(4ⁿー1ー3n)/4⌉と推定される。

(2)　状態準備　
　先の式を使うと、4 量子ビット(n = 4)の場合、忠実度= 1を達成するために必要な CNOT ゲートの最小数は N_min = 6 と推定される。つまり⌈(2⁴ー１ー４)/2⌉＝⌈(16ー１ー４)/2⌉＝⌈5.5⌉＝6となる。N_min = 6でも、量子回路の 8%は、忠実度= 1 である。N を増やすと、この確率は急激に増加し、N_min = 10 では、量子回路の 94% が 忠実度 = 1 である。言い換えると、n = 4 かつN_min = 10 の量子回路を(乱数生成器を使って)ランダムに生成すると、量子回路は、ほぼ確実に(94%の確率で)忠実度が1である。ただし、1量子ビットの回転パラメータは、最適化済みとする^✒4。
　n=5の場合、N_minは、⌈(2⁵ー１ー5)/2⌉＝13となるが、ランダムな量子回路を100個作成しても、忠実度＝1は実現できなかった！　ただし、N_min＝14にすると、 量子回路の 13%で、忠実度= 1が達成された。つまり、推定値は1だけズレていた。この微妙なズレは、n ≥ 5 では常に発生し、n=6ではズレ1。n=7,8だとズレ2となる。
✒4　最適制御アルゴリズムである、GRAPE(Gradient Ascent Pulse Engineering)アルゴリズムの修正バージョンを使用して最適化されている。最適化手順は最大 10⁵回繰り返される。忠実度が 1 − 10⁻¹² を超えるか、10³ 回の反復で 10⁻¹²未満しか増加しない場合、アルゴリズムは早期終了する。

(3)　ユニタリ演算子
　n=4の場合、忠実度= 1を達成するために必要な CNOT ゲートの最小数N_minは ⌈(4⁴ー1ー3×4)/4⌉＝⌈60.75⌉＝61と推定される。しかし、ランダムな量子回路を100個作成しても、忠実度＝1は実現できなかった！N_min＝62にすると4%、65にすると76%で忠実度＝1が達成された。
　n=5の場合、N_minは ⌈(4⁵ー1ー3×5)/4⌉＝⌈252⌉＝252であるが、259で初めて、忠実度＝1が達成された。266では80%の量子回路で忠実度＝1が達成された。

【4】考察　
(1)　本論文によると、状態準備の場合かつn=5の場合、１つのゲート配置に係る時間は約5分でゲート配置の数は10¹³である。1年は365日×24時間×60分なので、およそ5×10⁵分である。ゲート配置にかかる時間(分)＝5×10¹³を年換算すると、5×10¹³/(5×10⁵)≃10^８＝１億年となる。
　ユニタリー演算子合成の場合は、n=3でも、10×4.8×10⁶/(5×10⁵)＝2×4.8×10≃100年かかる。n=4になると 60×10⁴⁷/(5×10⁵)＝12×10⁴²年となって、実際の意味はないほど大きな数字になる。
(2)　本論文の方法では、忠実度= 1を達成するために必要な CNOT ゲートの最小数がピッタリは算出されない(ズレが発生する!)。しかし、目安を与えるだけでも、十分意味がある。地味であるが、重要な研究成果だと思われる。

【0】はじめに
　量子技術研究界隈は、人工知能研究(を襲った冬の時代)を他山の石[*A-16]とすべく、大言壮語を避け、合理的な予測を語り始めた。マイクロソフト･テクニカルフェロー兼量子部門バイスプレジデントMatthias Troyerが、｢量子コンピュータが優位性を示せるのは『計算化学と材料科学』のみ｣と該社公式ブログに投稿したのは、ほぼ1年前の23年5月1日であった(内容は、こちらを参照)。ここまで強い主張に対しては議論の余地ありだろうが、量子加速に関する研究が、｢主に、暗号解読と量子化学の2つの分野に集中している｣であれば、ほぼ肚落ちであろう。そこに一石を投じた研究が以下である。
　東京大学他[*A-17]の研究者は、｢物性シミュレーションでは、暗号解読や量子化学よりも少ない物理量子ビット数で、量子優位性が発現する｣と主張する論文[*A-18](以下、本論文)を発表した(24年4月29日@npj quantum information)。ちなみに、些細な誤植が若干存在する。

【1】本論文の主張
　本論文は、物性シミュレーションのお題¦P¦において、古典アルゴリズム¦C¦の実行時間と、量子アルゴリズム¦Q¦の実行時間を比較する。その上で、以下を主張する：¦Q¦の実行時間が、¦C¦の実行時間を下回る、物理量子ビット数は、10⁵のオーダーである。もちろん、付帯条件¦S¦が付く。具体的な¦P¦、¦C¦、¦Q¦、¦S¦の内容については、後述する(☛【3】(0))。
　いわゆる量子優位性が発現する規模(物理量子ビット数)を、量子化学で10⁶、暗号解読で10⁷とすれば、物性シミュレーション(¦P¦)で、量子優位性が真っ先に発現する、と結論付けている。量子化学の議論は”微妙”で、暗号解読の議論は”やや強引”と思われるが、結論は揺るがないだろう(☛【7】(1)及び(2)を参照)。

【2】事前整理
(0)　ゲート複雑性^⚔1
　特定の量子状態、またはユニタリー演算子を生成する^⚔2ことが、どの程度複雑であるかを示す尺度である[*A-19]。従って、特定の量子状態、または特定のユニタリー演算子を生成する^⚔2(再)ために、量子回路内で必要なプリミティブ量子ゲートの最小数によって与えられる。プリミティブ量子ゲートとは、入出力数が 1 または 2 となるゲートのことであり、量子回路の量子コストは、その構成に使われたプリミティブ量子ゲートの数である[*A-20]。
⚔1　量子回路複雑性とも呼ばれる。
⚔2　ある程度の誤差で近似する、でも良い。

(1)　古典アルゴリズム：テンソルネットワーク法　
0⃣　テンソルネットワーク法　
　テンソルネットワーク(TN)法の本質は、情報圧縮にある。TN法では、特異値分解(シュミット分解)を利用した、少数の”支配的な”特異値を抽出する。波動関数は、それら特異値に対応する基底関数を用いて、高精度に近似できる。量子状態は、当該基底関数を使って生成する縮約した密度演算子によって表現される。テンソルネットワークによる表現には、EPS(Entangled Plaquette State)やSBS(String Bond State)など、他にも沢山ある。
1⃣　DMRG( Density Matrix Renormalization Group：密度行列繰り込み群)　
　1次元系に最適と評価されるDMRGは、行列積状態(MPS)ベースの変分量子回路上で、変分最適化を実行する。縮約した密度演算子を使って基底状態のエネルギー期待値を表現し、変分法を使って(変分パラメータを最適化することによって)基底状態のエネルギー期待値を求める。縮約とは、テンソル間の積である。
　MPSは、1次元の境界則もつれ量子状態を効率的に捉えるように設計されているが、2次元系を含む、1次元を超える量子多体系にも適用できる。
2⃣　PEPS(Projected Entanglement Pair State)
　PEPSは、TPS(Tensor Product State：テンソル積状態)とも呼ばれる^⚔3。ちなみに、PEPSに和訳はないと思われる。DMRGとPEPSの違いはMPSとTPSの違いである。つまり本質的には、1次元と2次元の違いに過ぎない。
　DMRGは、2次元系にも適用可能であるが、基底状態エネルギーの精度を(同一に)保ちながら、系の サイズを増やすと、計算コストが指数関数的に増加する可能性がある。PEPS の計算コストは、系のサイズが増加するにつれて、多項式に増加すると予想される。このため、系のサイズが大きい場合には DMRG よりも効率的になる可能性がある。逆に言うと、系のサイズが小さい場合には、DMRGが効率的であると考えられる。
⚔3　テンソルネットワークは、さまざまな物理系に対して、多くの研究者が独立して、発見を繰り返していることもあり、呼び名が様々あったりする。

(2)　量子アルゴリズムー量子位相推定法　
　量子位相推定法(Quantum Phase Estimation：QPE)は、ユニタリー演算子の固有値を効率的に推定できる量子アルゴリズムである。波動関数の時間発展をシミュレートし(ハミルトニアン･シミュレーション)、時間発展で生じる位相差を補助量子ビットに書き込む。この位相差を、逆量子フーリエ変換で読み出すことで、与えられたユニタリー演算子の固有値の位相ϕを取得するように設計されている。なお、QPEは、古典アルゴリズムに対して、｢指数加速｣が保証されている。ただし、この場合の古典アルゴリズムは、完全配置間相互作用法(Full-CI法)である。
　QPEをエンド･ツー･エンドで、ステップに分解すると、次のようになる：状態準備→ハミルトニアン･シミュレーション(制御されたユニタリー演算子のべき乗演算)→逆量子フーリエ変換→測定(及び位相推定)。量子操作の文脈で、”制御された(controlled)”とは、量子ビット(制御量子ビットと呼ばれる)が、特定の状態にある場合にのみ、当該(制御)量子ビットに操作を実施することを言う。

【3】本論文のオリジナリティ
(0)　お題等の整理　
1⃣　¦P¦　
　本論文における物性シミュレーションとは、｢強相関量子多体模型において、基底状態エネルギーを求めること｣である。強相関量子多体模型は、2種類取り扱っている。❶2次元J₁-J₂ハイゼンベルグ模型と、❷2次元フェルミ･ハバード模型である。
　❶は、2次元正方格子上の最近接サイトと次近接サイトの相互作用のみを考慮したモデル(反強磁性モデル)で、幾何学的フラストレーションの効果が表現されている。量子スピン液体相が発現すると期待されているモデルでもある。
　❷は、量子物質における電子的･磁気的挙動の本質を捉えたフェルミオン模型の一つと評価されている。｢電子が固体中を量子力学的に運動できるという効果と、電子間に非線型な反発力の相互作用が働いている効果だけをギリギリ取り入れた、いわば極小モデル｣[*A-21]でありながら、超流動･超伝導、量子磁性など、さまざまな特徴を示す。極小モデルでありながら、2次元以上で、厳密解は得られていない。
2⃣　¦C¦　
　¦P¦に適用する古典アルゴリズムは、テンソルネットワーク(TN)法である。計算アルゴリズムとしてのTN法は、特異値分解(シュミット分解)を利用した、少数の”支配的な”特異値による近似というアプローチを採用する。量子(多体)系への適用であれば、少数の”支配的な”特異値に対応する基底によって生成される密度演算子を使った期待値に対して、変分法を適用する。具体的には、㊀DMRGと㊁PEPSが適用されている。
3⃣　¦Q¦　
　QPEである。反復量子位相推定法やベイジアン量子位相推定法ではなく、逆量子フーリエ変換を用いる、正統的なQPEである。
4⃣　¦S¦　
　㊀系のサイズ(格子サイズ)と㊁計算精度が限定された上での結論である。㊂状態準備と㊃測定の複雑性に関しては、ここでは、結論･頭出しだけ行う：他ステップの複雑性で抑えられる特定の物理系を対象とすることで、結果的に無視する。また、㊄古典計算には、高速化の余地が残されている。
㊀　系のサイズN_site(格子サイズは、N_site×N_site)は、❶に対して{4,6,8,10,12}、❷に対して{4,6,8,10}が考慮されている。結論が導かれるサイズの上限は❶❷ともに、10×10まで^❚補遺❚。
㊁　計算精度は0.01と設定されている。
㊂　状態準備の複雑性に関する詳細は、【5】(2)を参照。
㊃　測定の複雑性に関する詳細は、【7】(3)を参照。
㊄　比較対象となる古典計算には、どこまでのチューンが許されるのだろうか。GPUも使い、CPUも複数使って並列化し、イン･メモリー計算を行い･･･というセットアップだと、本論文の結論は成立しない可能性がある。
❚補遺❚
　❷に対して、厳密対角化の限界は20サイト前後で現れる。すなわち数値計算でも、近似なしでは、20サイト前後で限界が来る。本論文で考慮した格子サイズ{4,6,8,10}で言うと、6以上なら、6×6＝36＞20であり、近似あり数値計算が必要になる。つまり、格子サイズ10×10は、十分意味があることになる。

(1)　本論文のオリジナリティと論理構成　
　誤り耐性量子計算を前提に、量子アルゴリズムの実行時間をエンド･ツー･エンドで評価している。本論文での実行時間解析は、演算時間のみならず、状態準備に要する時間まで含めた”込み込み”時間を算出し、古典アルゴリズムと比較している。また演算時間(run time)も、いわゆるelapsed timeを使用している。elapsed timeとは、CPU稼働時間＋CPU及びCPU以外の待機時間、であり、本当の run time と見做されている。日本語では、経過時間と訳される。
　状態準備に要する時間まで含めた古典アルゴリズムとの比較が実施されていなかった理由は、状態準備に要する時間の解析が難しかったからである。本論文では、特定の(強相関)量子多体模型では、状態準備を効率的に行える(要する時間を多項式時間で抑えられる)ことを、数値シミュレーションの結果として示すことで、この壁を越えている。ここが、本論文のキモである。
　本論文の論理構成は、次のようなものである：(強相関)量子多体模型に対して、古典アルゴリズムと量子アルゴリズムの実行時間が同程度になる模型サイズを求める。そして、その模型サイズに対応する物理量子ビット数を算出する。この物理量子ビット数が、10⁵のオーダーであることを示し、量子化学計算や暗号解析に必要と見做されている物理量子ビット数よりも少ないことを確認する。
　物理量子ビット数の推定には、魔法状態工場の数や魔法状態工場の”床面積”も考慮されている(ので、最先端なのだろう。☛【6】参照)。

【4】古典アルゴリズムの実行時間解析　
　古典アルゴリズム(DMRGとPEPS)の実行時間は、実際にシミュレーションを実行して推定された。尚、GPUの使用及び複数CPUによる並列化は採用されていないが、採用すれば、高速化が可能であると推測されている(10倍程度の高速化を合理的に予想している)。
(1)　DMRGシミュレーションの実行時間推定　
　シミュレーションのハードウェア実行環境は、以下の通り：東大のスパコン(CPUは、AMD EPYC 7702。4コア)を使用して、マルチスレッド並列化を実施。クロック周波数は、２.0GHz。ソフトウェア実行環境は、ITensor^⚔4。
　系のサイズN_siteと結合次元の最大値D_max及び計算精度εによって、実行時間は異なる。計算精度εは、シミュレーションで得られる基底状態のエネルギー(以下、計算値)と、正確な基底状態のエネルギー(以下、厳密値)との差＝エネルギー誤差、に対して設定される。
❶　J₁-J₂ハイゼンベルグ模型　
　この模型に現れるパラメータは、J₁とJ₂である。エネルギー誤差ε＝0.01は、J₁(=1)に対して定められている(ようである)。
　㊀J₁=1.0、J₂＝0.0、㊁J₁=1.0、J₂＝0.5の場合が取り上げられている(㊁は量子スピン液体相の実現が期待されるモデルに相当する)。㊀㊁ともに、N_site＝10(つまり格子サイズは10×10)に対しては、D_maxが3000と設定されており、経過時間は10⁴秒オーダーと考えられる(㊀3.7、㊁7.9)。なお、N_site＝12及びD_max＝2500では、経過時間は10⁶秒オーダーと考えられる(㊀0.96、㊁1.3)。
❷　フェルミ･ハバード模型　
　この模型に現れるパラメータは、ホッピング係数tと、クーロン反発を表す係数Uである(一般的に、当該アルファベットが用いられる)。エネルギー誤差ε＝0.01は、t(=1)に対して定められている(ようである)。
　㊀t=1、U＝１、㊁t=1、U＝4、㊂t=1、U＝8の場合が取り上げられている(が㊀は規模が小さいので割愛)。㊁㊂ともに、N_site=10とすると、D_maxは㊁4500、㊂5000と設定されている。経過時間は、㊁7.1×10⁹秒、㊂3.7×10⁸秒である。
⚔4　量子多体系を、テンソルネットワークを使って解析するためのツールを提供してくれる、C++ライブラリ。

(2)　PEPSシミュレーションの実行時間推定　
　(厳密な)実行には、＃P困難問題を解く必要があるなど、PEPSシミュレーションの実行時間推定は難しい。一方で、先述の通り、系のサイズが小さい場合は、DMRGの実行時間が短いと考えられる。それを利用して、PEPSの実行時間が考える必要がない小さいサイズを対象にしている、と考えられる。
　念の為、環境だけ記しておく。シミュレーションのハードウェア実行環境は、以下の通り： 東大のスパコン(CPUはIntel Xeon Platinum 8280。28コア)を使用してマルチスレッド並列化を行った。クロック周波数は、2.7GHz。ソフトウェア実行環境は、 QUIMB^⚔5。
⚔5　量子多体系を、テンソルネットワークを使って解析するためのツールを提供してくれる、Pythonライブラリ。

【5】量子アルゴリズムの実行時間解析　
(1)　問題の在処ー状態準備のコストが問題である　
　本論文では、QPEを3つのステップに分解し、それに併せて、QPEを実行する量子回路のゲート複雑性Cを3つの項に分解する：C ～ C_SP＋C_HS＋C_QPE†。初項は、(量子)状態準備のコスト。次項は、制御されたハミルトニアン･シミュレーション^⚔6のコスト。最後の項は、逆量子フーリエ変換^⚔7のコストである。
　最後の項C_QPE†はO(log(N))であり、最も複雑性が低いとして無視される。ここで、Nは、物理量子ビット数である。第2項も、多くの場合^⚔8、 C_HS = O(poly(N))として評価されるため、ひとまず無視される。
　本論文は、第2項及び第3項に比べて『第1項のC_SPのスケーリングは、非自明である』として、その解析に全精力を注ぐ。
⚔6　所与のハミルトニアンHによる時間発展シミュレーションは、ハミルトニアン･シミュレーションと呼ばれる。つまり、exp(－iHt)で与えられるユニタリー時間発展演算子を使ったシミュレーションである(tは、時間変数)。
⚔7　量子フーリエ変換(QFT)・逆量子フーリエ変換を使わないQPE(例えば、ベイジアンQPE)も存在する。それは、｢QFTは、多数のゲート操作が必要であるため、量子誤りの蓄積を惹起｣し、｢量子誤り訂正を施した誤り耐性量子コンピュータ(FTQC)でなければ実行できない(と考えられている)｣ためである。つまりNISQマシン前提の議論である。ここでの議論は、FTQCが前提であるし、さらにQFTのコストが最も軽いので、QFTを使わないQPEという議論には意味がない。
⚔8　ハミルトニアンが疎であったり、局所的であったり、多項式で構成されている場合。

(2)　状態準備のコスト評価　
　本論文では、状態準備スキームとして一般的である、断熱状態準備(ASP)スキームを採用している。このスキームは、時間間隔t_ASPの時間発展を通して、基底状態を準備する決定論的方法である。具体的には、基底状態が、時間依存のシュレディンガー方程式によって、準備されるスキームである。
　まず、｢物性問題で重要な基底状態の多くは、多項式コストで容易に準備できると広く信じられている｣と身も蓋もないことを持ち出して来る(とは言え、そう信じられていることの物理的な理由は、物理的に重要な物性問題は｢平均場近似が、極めて良い近似である｣ことに由来している(はず))。本論文では、J₁-J₂ハイゼンベルグ模型並びにフェルミ･ハバード模型に対し｢数値的な発見｣を使って、この広く信じられている”コンセンサス”の裏付けを取っている。これは、あくまで数値的な発見を使って得られた結論であって、理論的に導出された結論ではない(ことは、明記されている)。
　上記した｢数値的な発見｣とは、ハイゼンベルJ₁-J₂グモデルに対してt_ASPの数値計算を行い、t_ASPにおけるスケーリング則が成立していることを、発見したことを指している。少し具体的に言うと、スケーリング係数β≒1.5が、J₁-J₂ハイゼンベルグモデルにおけるt_ASPのスケーリングに対して正確な予測を与えていた。
　このスケーリング係数を真とすれば(正確にはβ<2であれば)、C_SPはC_HSを越えないと考えられる(らしい)。正確には、β<2であればO(N^β/2) < O(N) ≤ O(poly(N))が言えるので、これを使って、C_SP < C_HSを主張していると考えられる。なおフェルミ･ハバード模型に対しては、β<2が明示されていないと思われるが、成立しているのだろう。

(3)　制御されたハミルトニアン･シミュレーションのコスト｜準備　
　特定の強相関量子多体系では、状態準備のコストは支配的ではないことが、数値的な発見により示された。従って、残りは、制御されたハミルトニアン･シミュレーションのコストである。つまり、以降は、制御されたハミルトニアン･シミュレーションの量子リソース推定を細かく行うステージである。量子リソース推定を行う前提は、以下の通りである：ユニバーサルゲート･セットは、クリフォード･ゲート＋Tゲート。量子誤り訂正符号は表面符号で、符号距離17～25(→21～25?)。論理演算は、ツイスト･ベースの格子手術^⚔9に基づいて構築される。物理誤り率は10^-3(標準的な設定値)。計算精度は10^-2。
　制御されたハミルトニアン･シミュレーションを実行するには、ユニタリー演算子のべき乗を計算する必要がある。教科書的に言うと、このべき乗計算には、鈴木･トロッター分解が使われる。本論文では、より新しい方法を含めた複数の手法を比べて、リソースを最も要しない手法を選択している。複数の手法とは、(ランダム化)トロッター積公式、qDRIFT、Taylorization法、qubitization法である(ここは、深堀しない)。また、この場合の量子リソースはTゲートの数である。
　いくつかの格子サイズにわたり、J₁-J₂ハイゼンベルグ模型(J₁=1.0、J₂=0.5)及びフェルミハバード模型(t=1、U=4)に対して、量子コンパイル(トランスパイル)を行い、Tゲートの数を計測した結果、qubitization法は最も、Tゲートの数が少なかった。qubitization法に対する和訳は、未だないと思われる(Taylorization法も同様)。
⚔9　格子手術は、誤り耐性量子コンピュータでマルチ量子ビットの論理演算を効率的に実現するための、最も有望な戦略であることが知られている。格子手術では、マルチ論理量子ビットの論理パウリ測定は、対応するブロックを適切な円周で接続することによって実現され、すべての論理クリフォード演算は、格子手術と論理アダマールおよび位相ゲートを使用した論理測定を介して、実行される。

(4)　制御されたハミルトニアン･シミュレーションのコスト｜実行時間の評価　
　適切な実行時間の見積もりは、ハードウェア構成^⚔10とコンパイル設定に大きく依存する。妥当なコストで実際の実行時間を推定するには、2 つの方法がある： ヒューリスティックな方法と、シミュレーションを用いる方法である。前者は、TカウントやT深さ^⚔11等の重要なパラメーターからヒューリスティックに実行時間を推定する方法。後者は、誤り耐性量子コンピューターのソフトウェア･シミュレーションを使用して、実行時間を計算する方法である。本論文では、後者つまり、シミュレーションを用いる方法が採用されている。
　格子手術演算用に論理量子ビットを再配置した量子回路に対して、シミュレーションを実行し、実行時間解析を行った^⚔12。その結果は、格子サイズ10×10のJ₁-J₂ハイゼンベルグ模型及びフェルミ･ハバード模型で、経過時間(elapsed time)は、概ね10^-4秒である。
⚔10　量子モダリティによって、大きく変わることは、容易に理解できる。
⚔11　Tカウントは、文字通りTゲートの数。T深さは、並列化可能なTゲートをグループと見做した時の、グループの数である。
⚔12　格子手術演算には、ターゲット論理量子ビットを接続する補助論理量子ビット セルが必要であるため、格子手術演算のスループットは、論理量子ビットの割り当てや、補助量子ビット･パスの配線などのトポロジ上の制約によって決まる。

【6】物理量子ビット数の評価　
　qubitization法を使ってTゲートの数を絞り、さらに格子手術用に論理量子ビットを再配置した量子回路を対象に物理量子ビット数の評価を行う。論理量子ビットの数をO(10²)、魔法状態工場^⚔13の数をO(1)、符号距離を≃20とする。さらに、本論文で行われている通り、魔法状態工場の床面積を176とすれば、物理量子ビット数はO(10⁵)となる。
⚔13　Eastin-Knillの定理より、量子誤り訂正符号はユニバーサルゲート･セット(本論文の場合は、Ｔゲート)を、トランスバーサルに実装できない。表面符号も例外ではない。表面符号で符号化した論理量子ビットにTゲート操作(非クリフォード演算)を行うためには、｢魔法状態｣を量子テレポーテーション回路を用いて、量子ゲート･テレポーテーションを実行する必要がある。この｢魔法状態｣の準備を繰り返すためだけに、量子ビット平面割り当てられた領域を、魔法状態工場と呼ぶ。
　なお、トランスバーサルとは、物理量子誤りが論理量子誤りに広がらない(あるいは、｢量子誤りが、量子回路全体に、制御不能に拡散しない｣)という意味である。

【7】考察　
(1)　暗号解読の議論について　
　暗号解読について、大規模×短時間であれば、2,000万量子ビット×8時間で2048ビットのRSA暗号(RSA2048)を解読できるらしい[*A-22]。小規模×長時間であれば、1万量子ビット×104日間でRSA2048を解読できるらしい[*A-23]。もちろん、2,000万、8時間、1万、104日という数字は、丸めた数字である。
　さて、暗号解読の量子優位性は、量子アルゴリズムが、2048ビットのRSA2048を古典アルゴリズムよりも速く解読できるという意味になる。スパコンでRSA2048を解読するのに10⁸年かかるらしい[*A-24]。本論文のロジックと平仄を併せると、比較すべきは、8時間でRSA2048を解読できる古典アルゴリズムである。そんな古典アルゴリズムは存在しないから、それ自体は無理である。一方、1万量子ビット×104日間と比較することは、可能である。つまり、2,000万～10⁷ではなく、少なくとも1万＝10⁴量子ビットで量子優位性が発揮される！そうすると、物性シミュレーションが最初に量子優位性を発現するという結果が覆る。しかし、それだと、10⁴量子ビットだと104日＝10³時間もかかるため、｢物性シミュレーションが『数時間で』量子優位性発現｣と平仄が合わない。
　『数時間』に相当する10⁷と比較するのが妥当とも言えないが、無理やり外挿して10⁵量子ビットに対応する時間を求めても、10²時間を要するから、物性シミュレーションが最初に量子優位性を発現すると言っても良いのだろう。
❚蛇足に近い、アップデート❚
(1)　RSA2048解読に要する物理量子ビット数に関して新しい動きがあるものの、上記(というか本論文)の結論は変わらないだろう。[*A-72]では、猫符号＋繰り返し符号で、{3.5×10⁵,4日}で解読と推定。[*A-73]では、猫符号＋LDPC符号で、{1.0×10⁵,7日}で解読と推定。[*A-74]では、yoked表面符号＋魔法状態培養で、{1.0×10⁶,7日未満}で解読と推定。
※　無理やり外挿した、10⁵物理量子ビットに対する10²時間(4日＝96時間、7日＝168時間)は、それほど悪くない推定であった。
(2)　加Photonic^🍁1は、自社開発したqLDPC符号｢SHYPS｣を使ったショアのアルゴリズムを実行するために必要な量子リソース推定(QRE)を行った(25年12月10日)[*A-110]。結果は{7.0×10⁶,3.9日}と一見平凡な結果である。ただし『初めて』分散型量子演算を想定してQREを行った。これまでは全て、モノリシック(＝分散型ではない)アーキテクチャを想定していた。Photonicはモノリシックは現実的でない(蛇足ながら、当社も同意見)から、該アーキ前提のQREも現実的ではない、と主張する。
　分散型で100万物理量子ビットの到達は、いつだろうか：1万×100(3～5年？) or 10万×10(5～7年？)
🍁1　シリコンにリン原子をドープして作成した欠陥＝T中心を量子ビットとして使う。T中心は、通信波長の光を放出する。つまりPhotonicは、シリコンT中心を光ネットワーク(実際には、量子もつれを形成する光子ペア)で繋ぐ、分散型量子コンピューティングを当初から志向している。ちなみに、マイクロソフトが投資している。

(2)　量子化学との比較について　
1⃣　本論文において量子化学計算に必要とされている物理量子ビット数10⁶については、一先ず深堀しない。本論文で扱った物性シミュレーションに必要な物理量子ビット数が、量子化学計算のそれより少ないことに、違和感はないと思われる。本論文で取り上げている量子多体模型は、シンプルなミニマム･モデルである。シンプルでミニマムであるにも関わらず、豊かな表現力を有するという、まさに物理好みのモデルである。故に、状態準備コストが小さいという結論にも、驚きはないだろう。
2⃣　ただし、その分、商業的価値は量子化学計算に劣るであろう。J₁-J₂ハイゼンベルグ模型は、量子スピン液体相を議論するには有用であろうが、商業的な価値を有する材料を作り出すモデルとはならないだろう。
3⃣　本論文でも言及されている通り、計算環境次第で、古典アルゴリズムはずっと速くなるだろう。そうなると、量子優位性が発現する問題のサイズ(格子のサイズ)は、大きくならざるを得ない。そうすると、量子化学に必要な物理量子ビット数10⁶に近接して、結論が微妙になるかもしれない。もっとも、古典計算の実行環境をバキバキにチューンする影響は、量子化学にとっても同様に作用するはずだから、順番自体に影響はないのかもしれない･･･
4⃣　ちなみに、量子化学計算に量子位相差推定法を使った場合、物理量子ビット数10⁶は、どういう影響を受けるのであろうか？
5⃣　量子化学計算と言っても、カバー範囲は広い。337頁に及ぶ量子アルゴリズムに関する広範なレビュー論文[*A-25]によると、必要と考えられる論理量子ビット数は、FeMo-Co^⚔14で200～2000程度。200とすれば、物性シミュレーションの論理量子ビット数と変わらない。シトクロームP450^⚔15、クロム2量体、ルテニウム触媒^⚔16、イブルチニブ^⚔17で10³なので、物理量子ビット数は10⁶ということになる。リチウムイオン電池材料や遷移金属触媒だと、おおよそ10⁴～10⁵なので、物理量子ビット数は10⁷～10⁸ということになるだろう。
⚔14　農業における窒素固定を担う｢土壌生態圏における生物窒素固定系｣で中心的な役割を果たす、真正細菌･古細菌が持つ窒素固定酵素｢ニトロゲナーゼ｣の活性中心に含まれる｢鉄とモリブデンを含む補助因子｣。
⚔15　一般的に、肝臓において解毒を行う酵素として知られている。
⚔16　様々な化学反応に用いられる触媒。例：医薬品の合成、アンモニア合成及びアンモニア(の窒素への)分解、NOx等の排ガス浄化、燃料電池電極など。
⚔17　B細胞性腫瘍の治療に用いられる、経口投与可能な抗がん剤。経口投与可能＝低分子＝必要な量子ビット数が少なくて済む。B細胞性腫瘍 ∊ 非ホジキンリンパ腫 ∊ 悪性リンパ腫。

(3)　測定(の複雑性)に関して
　【2】(2)で分解したQPEのステップは、状態準備、ハミルトニアン･シミュレーション、逆量子フーリエ変換、測定の4つであった。エンド･ツー･エンドを謳うのであれば、測定のコストも明示すべきである。結果だけ述べると、このコストはO(1/γ･1/ε)で与えられる。ここでγ＝|⟨ψ_ini|ψ_exact⟩|。|ψ_ini⟩は準備した初期状態、|ψ_exact⟩は厳密な量子状態(波動関数)。すなわちγは、｢厳密な量子状態｣に対する｢準備した初期状態｣の一致度(によって決定される数値)である。εは計算精度である。つまり、Nには依存しない。γ≃1、ε＝0.01としてO(10²)となる(し、その結果、無視できる)。
　ただし、これはポスト･セレクション^⚔18が効率的に行えることが前提であろう。そして、本論文で扱われた強相関量子多体模型❶及び❷は、該当するという理解で良いのだろう。いずれにしても、状態準備と併せて、｢10⁵オーダーの物理量子ビット数で、量子優位性が発現｣という結論の成立は、特定の物理系に限定されるということになるのであろう。
　なお、イコール･フッティングという意味で述べると、量子化学計算にも、状態準備と測定の議論は必要となる。状態準備と測定を考慮すると、10⁶は、益々限定的であろう。それどころか、エンド・ツー・エンドだと、現実的でない可能性もあるだろう。
⚔18　誤差のある測定結果を優先的に拒否し、誤差の少ない測定結果の部分を特定すること。

(4)　物性シミュレーション以外の物理的アプリケーションについて　
　為念･･･[*A-26]は、量子化学計算のQPE適用先として、固有振動数解析を提案している論文である。解析対象は、1次元に配置された質点が、バネでつながれた物理系である。量子演算を行う前提を『表面符号、符号距離23～27、格子手術に基づく論理演算、物理誤り率10^-3、計算精度10^-2』と設定した場合、質点数が{32,64}というサイズで、物理量子ビット数は10⁵オーダーになる(と推定されている)。先にあげた前提『･』は、本論文の前提と"全く"同じである(qubitization法が採用されている点も同じ)。なお、質点数が128になると、物理量子ビット数は10⁶オーダーになる(と推定されている)。

(5)　古典アルゴリズムについて　
　本論文で採用されている古典アルゴリズム｢テンソルネットワーク法｣の代替え手段としては、制限付きボルツマン･マシンが考えられるが、結論に影響は与えないだろう。

【0】はじめに
　大規模言語モデル等のバックボーンである生成AIモデルは、莫大なエネルギーを消費することが問題視されている。ChatGPT-3 の(事前)学習には電気代だけで、推定1億ドルを要する(とOpenAIのCEOが語ったらしい)。さらに、モデルの学習にかかるコストは10 か月ごとに倍増すると予測されている(らしい)。この問題解決につながる研究成果を、西マルチバース･コンピューティング他[*A-27]の研究者が示した。具体的に言うと、｢テンソルネットワークを利用することで、正解率(accuracy)を保ったまま、大規模言語モデル(LLM)のサイズ等を大幅に圧縮できた｣と主張する論文[*A-28](以下、本論文)を発表した(24年5月13日@arXiv)☛正確な意味は【1】を参照。マルチバースは、この圧縮技術をCompactifAIと名付けた(マーケティング、ブランディング)。なお本論文の成果は、量子LLMでもなく、量子インスパイアードLLMでもない。あくまで古典の範疇に留まる(故にAppendix)。テンソルネットワークを”量子にインスパイアされた古典的アルゴリズム”と呼ぶグループも存在する。
　この成果に対して、マルチバースは「AI-BOOST^†1による大規模 AI グランド･チャレンジにおいて、(マルチバースの成果を適用することで大幅に圧縮されることが期待される)LLM構築に、スパコンを使用する時間80万時間を獲得した｣と発表した(24年6月27日)[*A-29]。最低300億個のパラメータを持つ大規模LLMを開発する。
†1　AI-BOOSTは、欧州の人工知能(AI)コミュニティのベンチマークとなるよう設計された、オープン チャレンジ･プログラム。AI-BOOST の全体的な目的は、EU および関連諸国全体から才能ある人材を集め、AI の科学的進歩を推進することである。

【1】本論文の主張
　本論文は、以下を主張する：
(1)　テンソルネットワーク(TN)と量子化^†2を組み合わせることで、LLMのサイズ等を大幅に圧縮した。
(2)　(1)のサイズ等を大幅に圧縮したLLM(以下、本論文LLMと呼称)は、
　　　⓵　学習時間を、50%高速化
　　　⓶　推論時間を、25%高速化
する。
　TNとは、具体的には、行列積演算子(Matrix Product Operator：MPO)である。LLMは、具体的には、米メタが開発したLlama-2 7Bである(☛【2】を参照)。サイズ等の(大幅な)圧縮とは、以下⓷及び⓸を意味している。
　　　⓷　メモリサイズを、93%削減
　　　⓸　パラメータ数を、70%削減
(3)　LLMのサイズ等を大幅に圧縮した一方、正解率の低下は、⓹2～3%に抑えられた。
　なお、⓵及び⓶は、⓷及び⓸により、GPU-CPU転送時間が大幅に短縮されるために生じる(と説明されている)。
†2　深層学習の文脈における量子化とは、モデルの軽量化を目的として、計算機上で高精度表現されている数値を、低精度の数値で置き換えることを言う。とびとびの離散的な値しか取らない、前期量子論における”量子化”概念を踏襲している。現状一般的に使われる、古典⇆量子の意味での、量子化とは異なる。

【2】事前整理
(1)　Llama及び他LLMのパラメータ数　
　Llamaは、米メタが開発したLLMであり、オープンソースでところに、他LLMとの違いがある。Llama-2は、Llamaの第2世代である。2 兆を超えるトークンで事前学習されており、コンテキストの長さは 4096、100 万を超える人間の注釈による再学習が行われている。Llama-2には、パラメータ数が異なる3つのサブ･モデルが存在する。パラメータ数70億のLlama-2がLlama-2 7Bである(つまり最軽量モデル)。他には、パラメータ数130億の13Bと、700億の70Bがある。最新のLlamaはLlama-3で24年4月に公開された(パラメータ数は80億と700億)。
　参考までに、GPT-4のパラメータ数は5,000億～1兆と推測されている。NTTのtsuzumiは6億と70億、PFN(プリファード･ネットワークス)のPLaMo-13Bは130億と公表されている。ソフトバンクは、3,500億パラメータのLLMを開発する意向と報道されている。なお、サカナAIは、自社開発したパラメータ70億のLLMが、パラメータ数700億のLLMを凌駕したことを発表している^†3。
†3　https://sakana.ai/evolutionary-model-merge-jp/　

(2)　LLM用ベンチマーク　
1⃣　MMLU　
　MMLU＝Massive Multi-task Language Understanding(マルチタスク言語理解ベンチマーク)。カリフォルニア大学バークレー校、コロンビア大学、シカゴ大学、イリノイ大学アーバナ・シャンペーン校の研究者が開発した(2021年1月12日@arXiv[*A-30])。MMLU は、法律、医学、物理学など幅広い領域にまたがる 57 個のタスク、計 17,844 問の 4 択問題で構成されている[*A-31]。
2⃣　 HellaSwag　
　HellaSwag は常識推論用のベンチマークで、ワシントン州立大学とアレン人工知能研究所の研究者が開発した(2019年5月19日@arXiv[*A-32])。アレンとは、マイクロソフト共同創業者のポール･アレンのことであり、ワシントン州立大学はポール･アレンの母校(ただし、2年で中退)。機械(コンピューター)に常識を理解させることの難しさは、昔から有名である。[*A-32]には、｢人にとっては自明な(正解率^†495%超)常識問題でも、機械(人工知能)にとっては－それが例え最先端の人工知能であったとしても－正解率は48%未満に過ぎない、と書かれている。
3⃣　BoolQ　
　BoolQは、NQ^†5から派生した自然な yes/no 質問に焦点を当てたQAデータセット。BoolQは NQ より仕様を簡単化しており、yes/no のどちらかの答えをもつ質問文のみを採用し、文書全体ではなく 1 つの段落を質問文とペアにしている。non-factoid^†6な質問文が多く含まれており、解くために多様な推論能力が必要とされる[*A-33]。ワシントン大学とグーグルの研究者が開発した(2019年5月24日@arXiv[*A-34])。
4⃣　TriviaQA　
　TriviaQA は、クイズ問題集の Web サイトから収集されたクイズ問題に Web ページやWikipedia 記事を文書として付与した、読解型 QA のデータセットである[*A-35]。常識的推論(HellaSwag)と同じく、ワシントン州立大学とアレン人工知能研究所の研究者が開発したベンチマーク(2017年5月13日@arXiv[*A-36])である。
5⃣　GSM8K　
　GSM8K は、高品質かつ言語的に多様な小学校レベルの算数文章問題8,500問で構成されるデータセット。オープンAIの研究者によって開発されたベンチマークである(2021年11月18日@arXiv[*A-37])。
†4　正解率と訳した原語はaccuracy。
†5　NQ(Natural Questions)とは、人間の情報欲求から自然発生する質問からなるQAデータセット。
†6　non-factoid 型質問：理由や事象の説明に基づく正答を求める質問。factoid 型質問：名称や日付け･数値など事実に基づく正答を求める質問。出所：http://unicorn.ike.tottori-u.ac.jp/2008/s052014/paper/graduation-thesis/node16.html

【3】本論文の研究フロー
(0)　前説　
1⃣　概要
　本論文では、以下の3ステップを踏んで、本論文LLMを開発した：
㊀　ニューラルネットワーク･モデルにおける重み行列をMPOで置き換える。
㊁　MPOによる圧縮と量子化を併せて、 圧縮LLMを構築する。
㊂　圧縮LLMを、数回再学習する。
2⃣　特異値分解とMPO
　Llama-2 7Bの主な構成要素は 32 個のアテンション･ブロックである。各アテンション･ブロックは 4 つのマルチ･ヘッド･アテンション層と 3 つのMLP層で構成されている。MPOで置き換える重み行列とは、(モデルアーキテクチャ的には、トランスフォーマーでしかないLlamaの)デコーダー･ブロック内の自己注意(セルフ･アテンション)層及び、多層パーセプトロン(MLP)層の、重み行列である。
　難しいことはさて置き、ザックリ言うとMPOとは、すなわち行列の効率的な表現である。そしてMPOを決定するプロセスでは、特異値分解(SVD)を使用する。SVDは、処理対象とする行列の｢値が大きい、固有値｣を抽出する手段である。主成分分析の主成分(第一主成分、第二主成分)を抽出することと本質的には同じである。各重み行列に対して、連続的に特異値分解(SVD)を実行し、各 SVD で最大の結合次元のみを保持する。この結合次元の切り捨てにより、特定の層内のモデル･パラメーター間の相関関係が、最も関連性の高い相関関係だけに、効果的に切り捨てられる。

(1)　㊀→MPO　
1⃣　感度分析　
　アテンション･ブロックの位置に応じて、MPOで置き換えるシミュレーションを行った結果から、以下を推奨している：シミュレーションにおけるブロック位置は、0～31の中から、0,5,15,31を選択した。シミュレーションの結果、位置に応じてMPO置き換えに対する”感度”が異なることがわかった。感度が異なるとは、タスク^†7において、MPO置き換えに対する正解率(accuracy)の変化が異なるという意味である。具体的には、ブロックの先頭及び前半(0及び5)はMPO置き換えに敏感であり、ブロックの中間及び後半(15及び31)では感度が低下した。
†7　タスクとしては、MMLU(Massive Multi-task Language Understanding：大規模マルチタスク言語理解)を採用している。☛【4】(0)を参照。
2⃣　小括　
　結論として、先頭及び前半の置き換えは50% 未満にすることを推奨している。一方、中間及び後半では90%まで置き換え可能としている。さらに、MLP層は極めて敏感であり、MPOへの置き換えから除外することを推奨している。
3⃣　パラメータ数の削減割合の試算　
　32個のアテンションブロック前半16個の50%をMPOで置き換え→50%×16個＝8個。後半16個の10%をMPOで置き換え→10%×16個＝1.6個。(8+1.6)/32個＝30%。これをもって、パラメータ数70%削減としているのだろうが、正確には成立していないと思われる。　

(2)　㊁→量子化　
　オリジナルのLlama-2 7Bは、float-32、つまり32ビットの浮動小数点数である。本論文では、これに対して4種類の量子化を試行している。具体的に言うと、❶float-32→int-8、❷float-32→int-4、❸float-32→float-16、❹float-32→｢ミックス｣である。❶及び❷の量子化モデルは、bitsandbytes^†8量子化ライブラリ(フレームワーク)を使用した。本論文LLMは、｢重み行列のMPOによる置き換え＋❹の量子化｣を行って、⓵～⓹(☛【1】参照)を達成している。
　int-8(int-4)とは8ビット(4ビット)の整数である。 float-16は、16ビットの浮動小数点数。｢ミックス｣では、MPOで置き換えた層に対してはfloat-32→float-16を適用し、 MPOで置き換えなかった層に対しては float-32→int-4を適用する。
†8　量子化ライブラリ(フレームワーク)は、bitsandbytesとautoGPTQの2つがメジャーらしい。後者は、｢量子化に学習データを要する一方で、高速化できる｣。前者は、｢データ不要(なので手軽)｣らしい(参照：https://blog.shikoan.com/minigpt4-autogptq-quality/)。

(3)　㊂→再学習　
　圧縮LLMの構築後には、(数回の)再学習が不可欠である。その理由を本論文では次のように説明している：｢TNアルゴリズムのいわゆる”単純な更新”に似た、ローカルな層ごとの MPO への切り捨ては、特定の層の重み行列を切り捨てるときに、他の層の影響が明示的に考慮されないという意味で、一般に最適ではない可能性があるためである｣。ただ、この再学習は、モデル パラメータ数が大幅に少ないため、元モデルの学習よりもはるかに効率的である。故に、再学習を行っても本論文LLMは、サイズ等の大幅な圧縮が可能とされている。
　なお、再学習^†9には、Ultrachat^†10、Alpaca^†11、OpenHermess^†12 などの汎用チャット･データセットが使用された。
†9　healingという再学習手法を使用したらしい。再学習の詳細は(意図的に?)明らかにされていない。
†10　Ultrachatは、ChatGPT Turbo APIを利用した、オープンソースの大規模･多ラウンド対話データセットらしい(出所https://note.com/npaka/n/nf71d2eb2fb25)。
†11　Alpacaデータセットは、Alpaca 7Bの再学習に用いられたデータセット(らしい)。Alpaca 7Bは、米スタンフォード大学の研究者が、LLaMA 7Bモデルを再学習したモデルである。出所：　https://crfm.stanford.edu/2023/03/13/alpaca.html。
†12　詳細不明。

【4】検証結果　
(1)　概要　
　⓪オリジナルのLlama-2 7B、①MPOによる重き行列の置き換え＋量子化❶、②MPO＋❷、③MPO＋❸、④MPO＋❹＝本論文LLM、が比較検証される。
1⃣　指標　
　比較検証に用いられた指標は、正解率(accuracy)と学習時間及び推論時間である。　
2⃣　タスク　
　正解率に関しては、以下5つのタスクに対して検証を行った：言語理解(MMLU)、常識的推論(HellaSwag)、読解(BoolQ)、世界知識(TriviaQA)、数学(GSM8K)。学習時間に関しては、 MMLUに対してのみ比較検証を行った。推論時間は、5つのタスクに対して行った。

(2)　結果　
1⃣　正解率　
　5つのタスク全てに対して、正解率は⓪＞①＞②＞③＞④である。世界知識で、差(⓪～④)が最も小さく(グラフの目視で1%程度か)、 数学で差が最も大きい(グラフの目視で3～4%)。
2⃣　時間　
　学習時間は、⓪～②が20分。③及び④が11分程度なので、⓪→④で50%高速化としている(正確には、45%程度か)。
　推論時間の結果は、やや複雑である。まず定性的に言うと、3つのグループに分かれて、②が最も悪く(時間がかかる)、⓪と①は同程度で、③と④が速い。タスク別に言うと、 HellaSwag 以外の全てで、 ④＞③＞①＞⓪＞②。HellaSwagのみ③＞④＞⓪＞①＞②、である。定量的に言うと、②は1.1～1.2ミリ秒。⓪及び①は、概ね1ミリ秒を下回る程度。③及び④は、概ね0.7ミリ秒程度である。この結果から、推論時間については、⓪→④で25%高速化としている。

【5】考察　
(1)　本論文の駆動力は、次の２つと推量される。
1⃣　枝刈り、知識蒸留^🐾1、低ランク近似などの従来の”圧縮方法”は、ネットワーク内の有効なニューロン数を減らすことに重点を置いている。また、量子化は、ニューロン数を固定したまま、モデルサイズを縮小するために個々の重みの数値精度を下げることに重点を置いている。これらの”圧縮方法”は実際には比較的成功しているが、ニューロン数を切り捨てることが最適な戦略であると信じる説得力のある理由はない。
🐾1　学習済みモデルの予測結果を学習目標として、他のモデルを学習させる手法。蒸留を使うことで大きなデータセットを大きなモデルで学習し、その結果を小さなモデルに移すことが可能となる。出所：https://xtech.nikkei.com/atcl/nxt/mag/rob/18/00007/00040/
2⃣　標準的な LLM は、実際には過剰にパラメータ化されている(と考えられている)。つまり、パラメータ数を増やせば増やすほど性能が高まる、というわけではない可能性がある。
　その上で、
3⃣　本質的に重要である小数の物理量で記述できるであろう現実的な物理系では、比較的少数の特異値のみを考慮して縮約したテンソルが、十分に良い近似となっていることが知られている。
ので、LLMの重み行列をテンソルネットワークを使って、(試しに)情報圧縮してみた。本論文は、そういうことであろう。なぜ大幅圧縮できたか？は、結果的に、｢2⃣標準的な LLM は実際には過度にパラメータ化されている｣ことを是とすれば、説明できるのだろう。

(2)　もっとも、サカナAIは、パラメータ数を1/10(700億を70億)にしても、性能が落ちるどころか、むしろ凌駕すると言っている。それに比べれば、本論文LLMは、｢⓸パラメータ数70%減で、⓹正解率2～3%落ち｣であり、｢若干ショボく｣感じる。
　ついでに【1】の⓵～⓹について評価すると、以下のようになるであろう：⓵は、やや誇張。⓶は、誇張なし。⓷は、定量的な証拠は示されていない。⓸は、誇張あり。⓹は、誇張なし。→さらにショボい？　
👉　別の評価軸－例えば、作話(confabulation。一般的には、ハルシネ－ションと呼ばれる)について、本論文LLMとサカナAIのLLMでは、どうなっているのだろうか？　

(3)　ちなみに、スイスの"総合"量子スタートアップであるテラ･クォンタム(TQ)も、LLM圧縮に関する論文[*A-38]を発表している(24年1月29日@arXiv)。こちらも、重み行列を圧縮するが、手法は｢一捻りを加えた｣クロネッカー分解である。TQの手法をGPT-2_smallに適用したTQCompressedGPT-2は、パラメータ数を1億2400万個から、8100万個に減らした(!)。Wikitext-2、Wikitext-103、および Lambadaデータセットを使って、GPT-2_small、KnGPT2^🐾2、DistilGPT2^🐾3と比較した。ただし、学習データ量が揃っているのはKnGPT2のみ。パープレキシティを指標として、KnGPT2とTQCompressedGPT-2とを比較すると、TQCompressedGPT-2が、1.71%～4.48%下回る(😓)。
🐾2　GPT-2をクロネッカー分解したモデルらしい。
🐾3　知識蒸留したGPT-2らしい。

(4)　本論文LLMを再現(自身でスクラッチから構築)しようとした場合、再学習の部分がネックとなるのだろう。

【0】はじめに
　仏パリ･サクレー大学^🐾1及び米クオンティニュアムの研究者は、｢NISQ 時代の実装に有望な分野を特定し、量子優位性を強化する主要なアルゴリズム･プリミティブ^🐾2を特定する｣ことを目的として、量子アルゴリズムを分類した論文[*A-39](以下、本論文)を発表した(24年7月6日@arXiv)。ただし、本論文は、サプライズ、あるいは新たなインサイトを提供してくれる論文ではない。結論には総じて、既視感がある。
🐾1　仏の高等教育･研究機関の構成は、外部から見ると複雑である。大学の他に、グランゼコールという仏独特の機関が存在する。そのため、英タイムズなどが発表する世界大学ランキングには、仏が誇る科学技術力が適切に反映されていない、という不満が(仏国内に)あった。そこで、世界ランキングを上げるために、国策で作られた大学(の一つ)が、パリ・サクレー大学である。パリ・サクレー大学は、科学技術分野に特化している。タイムズによる最新(2024年度版)のランキングで世界58位(京大は55位)。仏トップは、PSL研究大学の40位(日本のトップ東大は29位)。
　パリ・サクレー大学の前身であるパリ第11大学は、12人のフィールズ賞受賞者を輩出しているらしい。未だに、実力と評価はマッチしていない。
🐾2　素朴に説明すると、｢基本的な構成部品｣という意味合いである。ソフトウェア寄りの表現を使うと、｢他のサブルーチンを使用していないサブルーチン(メイン･サブルーチン)｣となる。サブルーチン界の｢素数｣という見方もありだろう。

【1】本論文の推測
　本論文は、次のように推測している：
　量子特異値変換(QSVT)が、将来的に重要な役割を果たす可能性が高い。・・・So what?という感じが拭えない。

【2】本論文の概要及び構成
(0)　概要　
　本論文と既存類似研究との大きな違いは、｢(本論文は、量子アルゴリズムが古典アルゴリズムよりも)計算量が少ない、という箇所には焦点を当てていない｣という点である。代わりに、134個の量子アルゴリズムを、それらが解決する、(1)基本的な数学問題、(2)実際のアプリケーション、それらが使用する(3)主要なサブルーチン等に従って分類した。さらに、サブルーチンの分類に従った分析から、 量子アルゴリズムの依存関係を確立した。そうすることで、主要な確立されたアルゴリズム･プリミティブと、新しく出現したプリミティブの両方を識別した。
　134個の量子アルゴリズムは、文献レビューに基づくアプローチで選択した。選択プロセスでは、量子コンピューティング界隈で高く評価されているアルゴリズム、長年に渡って量子コンピューティング分野の進歩に大きく貢献してきたアルゴリズムを優先的に含めた。新しいアルゴリズムは、論文における引用頻度に基づく人気で選択した。従って、選択プロセスには、ある程度の恣意性が残ることは避けられない。

(1)　基本的な数学問題　
　基本的な数学問題については、以下6 つのクラスを特定した：㊀隠れた部分群問題、㊁線形代数、㊂動的システム(力学系)、㊃確率過程と統計、㊄最適化、㊅組み合わせ論。　

(2)　実際のアプリケーション　
　実際のアプリケーションについては、以下6 つのアプリケーション･ドメインを抽出した。
①　暗号解読
　補足は不要であろう。
②　機械学習とデータ･サイエンス
　ここには、i)分類、回帰、クラスタリングなどのタスクの実行、およびii)データ分析、統計モデリング、または大規模データセットを管理するための予測分析の分野における量子アルゴリズムの応用が含まれる。たとえば、推奨システムのための量子アルゴリズムは、これら両方の分野に応用されている。
③　第一原理量子シミュレーション
　第一原理(あるいは、非経験的)量子シミュレーションとは、量子力学的記述に基づいて解析系の物理的特性をシミュレートおよび予測することを指す。経験的モデルやパラメータ･フィッティングを介した迂回は行わない。第一原理量子シミュレーションには、電子構造や原子核構造、または材料特性の解決が含まれる。
④　古典的な科学技術計算
　このドメインは、第一原理量子シミュレーションではない科学計算アプリケーション(経験的モデリング･アプリケーションや、データ/信号処理アプリケーションなど)に対応するために使用される。このドメインに属する量子アルゴリズムは、古典力学シミュレーション、経験的/半経験的数値モデル予測と最適化、実験データ処理/マイニングなどの特定のタスクで、古典アルゴリズムよりも優れている”可能性がある”。
⑤　オペレーションズ･リサーチ(OR)　
　キーワード的に表現すると、数理計画法、最適化、ゲーム理論アルゴリズムが、このドメインに属する。平たく言うと、｢モデリング、統計、最適化｣等の分析手法を使用して、複雑なシナリオ下での意思決定問題^🐾3に対する最適(または、ほぼ最適)なソリューションに到達することが含まれる。
🐾3　物流最適化、サプライチェーン･マネジメント(SCM)、リソース割り当て(人員資源割り当て等)、等が該当する。
⑥　量子イネーブルメント
　このドメインは、多くのより具体的な量子アルゴリズムの基礎となる、一般的なアルゴリズム設計のアイデアを表すことが多い。例えば、量子テストアルゴリズムはこのドメインに分類される。

【3】量子アルゴリズムの依存関係ネットワーク
(1)　現状・・・｢四天王｣の時代　
　依存関係ネットワークには、4 つの大きなクラスターが、明らかに存在する：㊀量子フーリエ変換 (QFT)、㊁量子振幅増幅法(AA)、㊂断熱量子計算(QA)、㊃変分量子固有値ソルバー(VQE)である。本論文には、｢この研究で採用された方法論を通じて、これらの 4 つのプリミティブが”コア”として浮上したことは、量子アルゴリズムの実践者が期待するものと一致しており、興味深く、安心できる｣と書かれている。つまり、本論文における方法論の妥当性が検証された、と述べている。
　QFTは、QFTベースの量子位相推定法(QPE)^🐾4を使用したショアのアルゴリズムの基盤であるからコアとして抽出された、と考えられる。AAは、グローバーのアルゴリズムの基盤である。言うまでもなく、ショアのアルゴリズムとグローバーのアルゴリズムは、言わずと知れた、超有名な量子アルゴリズムである^🐾5。
🐾4　QFTは量子リソースを喰うので、ベイジアン量子位相推定法のようなQFTを使用しないQPEが登場している。
🐾5　ショアのアルゴリズムは、指数加速が、”極めて強く期待”される。期待の意味は(二重否定構文で回りくどいが)、｢ショアのアルゴリズムより速い古典アルゴリズムが存在しない｣ことは、数学的に証明されているわけではない、という意味である。グローバーのアルゴリズムは、2次加速が｢数学的に証明されている｣。ただし残念ながら、”無条件というわけではない”。

(2)　将来・・・どのプリミティブが最も支配的になるか？　
　本論文では、｢量子特異値変換(QSVT)が、将来的に重要な役割を果たす可能性が高いと思われる｣と推測している。その理由として、｢QSVTは、有名な統一アルゴリズム｣^🐾6であり、｢QSVTは、他の主要なアルゴリズムのほとんどを、特別なケースとして包含する｣^🐾6(再)こと並びに、｢QSVTは、量子アルゴリズム設計に対する”現代的な”アプローチ、つまり量子コンピューターを使用して、適切な入力に適用された指数関数的に大きな行列の固有値または特異値を操作するというアプローチを捉えたフレームワークの役割を果たす｣ことを上げている。ちなみに例えば、量子トランスフォーマー･モデルの構築^🐾7にもQSVTが使われる。
　なお、脱量子化の影響は、QSVTにも及ぶがそのインパクトの推定は難しい、と既述されている。
🐾6　QPEやHHLアルゴリズム、グローバーのアルゴリズムといった量子アルゴリズムを統一的に理解できるアルゴリズム、という意味である。他の主要なアルゴリズムのほとんどを、特別なケースとして包含する、ことと繋がる。
🐾7　トークン･ユニタリ(ユニタリ行列として符号化された、ベクトル化トークン)の重ね合わせを作成する非線形変換に、QSVTを使用する。

【4】アルゴリズムⓍ基本的な数学問題＆アプリケーション
(1)　総論　
　新しいアルゴリズムの数が増加しているアプリケーション･ドメインは、(目視で)第1位｢機械学習とデータ･サイエンス｣、第2位｢第一原理量子シミュレーション｣、第3位｢オペレーションズ･リサーチ ｣。暗号解読ドメインは、新しいアルゴリズムの数の加速という点で、最もゆっくりと推移しているドメインである。

(2)　各論
1⃣　QPE　
　動的システム･クラスの問題を解く場合、QPE は基底状態エネルギーを推定する基本的な方法を提供する。線形代数クラスの問題を解くことを目的としたとき、QPE は初期の｢量子線形システム･アルゴリズム：QLSA｣(つまり HHLアルゴリズム)のサブルーチンとして機能した。
　その後のQLSAは QPE を回避し、AA、QA、QSVTなどの他のプリミティブとサブルーチンを使用する。使用するプリミティブやサブルーチンが何であれ、多くの問題は線形方程式で定式化できるため、QLSA は線形代数、最適化、確率過程と統計、動的システム･クラスの問題の解決に役立つ。
2⃣　QAE(量子振幅推定法)
　QAE も、QPE と AA を組み合わせることによって初めて得られた。 QAE を使用すると、重ね合わせ状態内の状態の振幅を推定できる。振幅符号化を使用し、振幅によって符号化された情報を取得する必要があるアルゴリズムの基本プリミティブとして機能する。つまり通常は、組み合わせ論クラスの問題の解決に役立つ。
　QAE は確率微分方程式や一部の量子機械学習タスクを解くためにも使用される。さらに、QPE のない QAE が登場した。これは、他のアルゴリズムによって数値計算を実行し、線形代数、最適化、確率過程と統計、動的システム･クラスの問題を解決するために使用される。
3⃣　QSVTとQSP(量子信号処理) 　
　QSVT と QSP アルゴリズムの最終的な影響は、大きくなると予想される。これは、HHLアルゴリズムにおける初期のサブルーチン使用の多くが、QSVTをサブルーチンとして使用する高度なQLSAに、直接置き換え可能であることに限定されない。QSVTをハミルトニアン･シミュレーション(HS)に使用することで、最適な計算複雑性が得られることがあるからである。さらに、固有値変換や(任意のチェビシェフ多項式の)フィルタリングのような強力な機能は、探索が進めば進むほど、より多くの用途が見つかる可能性がある。
4⃣　ハミルトニアン･シミュレーション(HS)　
　HS アルゴリズムは、線形代数クラスの問題に加えて、動的システム･クラスの問題にも対応している。HS アルゴリズムは、ほとんどの場合、第一原理量子シミュレーション･ドメインで適用される。
5⃣　変分量子アルゴリズム(VQA)及びVQE　
　VQEは、演算子の固有値を見つけるために設計されたアルゴリズムであり、量子系の基底状態エネルギーを見つけるためによく使用される。分子の電子構造をシミュレートするなど、化学や材料科学に適用され、動的システム･クラスの問題を解決するために、VQEをメイン･サブルーチンとして使用する。その結果、第一原理量子シミュレーション･ドメインでは、VQEの使用率が高い。
　ただし、組合せ論及び、最適化クラスの問題に対するVQAの増加により、ORドメインでもVQEの使用率がかなり高い。VQE の開発に続いて、変分原理に基づく多数のVQAが開発された。これらのアルゴリズムは、基底状態エネルギーの計算を超えて、数値最適化及び、線形代数クラスのより広範な問題を解くことができる。
6⃣　QAとQUBO(2次制約なし二値最適化問題)　
　線形代数及び、数値最適化クラスの問題を解く場合、QA アルゴリズムの重要な使用法の 1 つは状態準備である。これは、QLSA のサブルーチンとしてよく使用される。QA アルゴリズムの別の使用法は、組み合わせ論クラスの問題を、ヒューリスティック的に解くことである。Ising-QUBO定式化と QAOA(量子近似最適化アルゴリズム)が、多くの NP 問題の解を Ising型スピン ハミルトニアンの基底状態に符号化する、統一された方法を提供する。巧妙に設計された断熱時間スケジューリングにより、断熱ハミルトニアンの最小エネルギーギャップを合理的に操作することができ、時間計算量の利点が可能になる。

❚ はじめに ❚　
　中国の研究機関である浙江ラボ(Zhejiang Lab)の研究者は、｢グラフ量子ウォーク･トランスフォーマーが、他のグラフ分類アルゴリズムよりも優れている｣と主張する論文(以下、本論文[*A-41])を発表した(24年12月3日@arXiv)。
　グラフニューラルネットワーク(GNN)と比較して、グラフ･トランスフォーマー(GT)はグラフ内のすべてのノード間のペアワイズ関係を考慮する。そのおかげで、各ノードは、他の全ノードに直接注意を向けることができる。この性質により、GTは遠く離れたノードの情報(グローバル情報)を捕捉することが可能であり、表現力が大幅に強化される。ただし、課題も存在する。本論文は、まず課題を整理し、次に解決策を提示する。解決策を実装したGTが、グラフ量子ウォーク･トランスフォーマー(GQWformer)である。
　代表的なデータセットを使ってベースラインと比較し、GQWformerが優れていると主張する。ただ、これは、古典→量子で性能があがる、という類の話とは限らない(☞❚ 考察 ❚)。

❚ 課題 ❚　
(1)　GTは^🐾1、グローバル情報の捕捉に優れる一方、ローカル情報の捕捉に難がある。ローカル情報とは、グラフの構造情報^🐾2である。
(2)　GTは^🐾1、ノードにおける特徴量の情報を考慮していない。
(3)　過剰グローバル化問題：既述の通りGTは、グローバル情報の取り込みに優れる。しかし、遠方ノードからの冗長な情報が蓄積されると、それは有害になりうる。そもそも近隣ノードは、｢より有用な情報を持つ(短距離相互作用の方が影響が大きい)｣はずであり、グローバル情報を｢過度に｣取り込まない方が良い、と考えられる。
🐾1　本質的には、｢トランスフォーマーのアーキテクチャは｣という文言で置き換えられる。
🐾2　グラフG＝(V,E)とした場合、φ(e)＝(u,v)を満たす写像φ、e及び(u,v)の組をグラフの構造情報と呼んで良いだろう。なぜなら、グラフは、V,E及びφで完全に規定できるから。ここで、e ∊ E、u,v ∊ Vである。

❚ 解決策 ❚　
(課題 1)→(策1)　注意スコアの計算を、クエリQとキーKの内積だけで行わない。本質的には、頂点Vと辺Eに各々重みをおき、その積をに加えて、注意スコアを計算する。
〚補足〛辺に置く重みは、ある頂点から別の頂点に移動するときに、該当する辺を選択する確率を表す。頂点に置く重みは、頂点が選択される確率を表す。GQWformerにおいて、当該重みは、量子状態の複素振幅の自乗という形で、ネイティブに導入される。頂点と辺における重みは、グラフの構造情報と解釈可能である。
(課題 2)→(策2)　隣接ノードの特徴量に基づいて、各ノードv_iで異なるコイン演算子^🐾3を生成する関数g(v_i)を考える。
🐾3　ランダム･ウォーク及び量子ウォークの文脈におけるコインとは、次に移動する頂点を決めるために、投げるコインを意味している(し、コインを投げることを仄めかしている)。量子ウォークの場合、量子コインとも呼ばれる。言うまでもなく、量子コインは演算子である。なお、本論文における量子ウォークは、離散時間量子ウォークである。
(課題 3)→(策3)　QWは、その長さを決めることで、各ノードの相互作用の範囲が決めることができる。つまり、モデルの受容野を柔軟に調整することができる。本論文では、感度分析を行ってQWの長さを検討した結果、最も高い精度を達成した、長さ4と決定している。
✚ その他工夫　
㈠　GQWformerは、自己注意モジュール＋再帰モジュールで構成されている。(策1)の枠組みは、頂点間を移動する場合に辺を選択する確率を考えている。例えば、頂点をuとvとしよう。この場合uからv(仮に順方向)と、vからu(仮に逆方向)は、区別すべきであろう。再帰モジュールでは、双方向GRU(Gated Recurrent Unit)を用いて、順方向量子ウォークの学習と逆方向量子ウォークの学習をそれぞれ行い、プーリング操作を行いマージさせている。
　本論文ではアブレーション分析の結果、再帰モジュールを次のように評価している：QWシーケンスに固有な時間的及び順序的な依存性を活用して、グラフ構造情報の詳細に焦点を当て、GQWformer のパフォーマンスを強化している。
㈡　グラフに特別なノードを追加し、それをグラフ内の他のすべてのノードに接続している。この仮想ノードは、ノード間の効率的な情報交換を促進し、全体的なパフォーマンスを向上させる。さらに、仮想ノードはグラフ内のすべてのノードからの情報を集約するため、その隠れた特徴量をグラフ全体の埋め込みとして採用し、下流のタスク用に追加の分類器を学習する。

❚ 性能ーベースラインとの比較 ❚　
　分類タスクにて、比較を行っている。
(1)　セットアップ　
1⃣　データセット　
　1 つの生物学データセット(PROTEINS)、2 つの化学データセット(MUTAG と PTC)、および2つの社会学データセット(IMDB-Bと IMDB-M)を含む、5つのTUDataset^🐾4を使用する。10分割交差検証を使用して学習セットとテスト セットを選択する。各データセットについて、グラフセット G 全体が指定されると、G の 90% を学習セットとしてランダムに選択し、残りをテスト セットとして使用する。
🐾4　主にGNNやグラフ･カーネルの研究向けに整備された、多数のグラフ･データから構成されるデータセット。TUDatasetのTUDとは、このデータセットを作成したTU Dortmund University(独ドルトムント工科大学)を意味している。
2⃣　ハイパーパラメータ等　
　最終学習率が 1×10⁻⁹ の線形学習率スケジューラを使用する。GQWformer のオプティマイザーは、重み減衰が 0.01 の AdamW である。勾配爆発のリスクを軽減するために、勾配クリッピング値を 1 に設定する。ドロップアウト率は 0.1。
　先述の通り、QW の長さは 4 に設定され、GQWformer ブロックの数も 4 に設定される。
3⃣　べースライン　
　11 のベースラインと比較する: DGCNN、IGN、GIN、PPGNS、Natural GN、RWNN、CRaWl 、CIN、GSN、GNN-AK、RWC。

(2)　結果　
　劇的な結果は出ていない。GQWformerの性能が、やや上回る程度であるが、そのほうが信頼性がある。化学データセットの場合、GQWformer はすべてのベースラインよりも、MUTAG で少なくとも 0.5%、PTC で 2.3% 精度が優れている。生物学データセット PROTEINSでは、精度を 1.3% 向上させ、社会学セータセットでは IMDB-Bで 0.5%、IMDB-Mで 0.8% の精度向上を達成している。

❚ 考察 ❚　
(0)　11ものベースラインに対して勝っているのだから、凄いと言っていいのかもしれない。
(1)　量子技術の導入によって性能が上がったという見方は微妙だと思われる。量子ウォークは、ランダムウォークとは｢数学的な意味で、質的に異なる｣確率分布を導入できる。質的に異なった確率分布を導入したことによって、古典的手法とは質的に異なる探索が行われた結果、分類タスクの精度が向上した、というなら、量子技術が分類精度をあげたと言って良いだろう。
(2)　しかし、GQWformerにおける策1は、(自己)注意機構に注意バイアスを入れ込むことで、達成されている。本論文では、注意バイアスは量子符号化の下で計算されているわけだが、注意バイアス自体は、古典的にも算出可能と思われる。もちろん、量子的注意バイアスと古典的注意バイアスは異なる値になるだろうが、その差は、注意バイアスの有無に比べて、どれだけ大きいかは、やや疑問。
(3)　策2は、ノードにおける特徴量に応じてコイン演算子を変えているが、この｢制約｣は、量子ウォークの質的に異なる確率的性質を、制限しているのではないかと推量する。策2も古典的に再現可能と思われるが、｢制約｣を受けることで、さらに、古典的な再現との差が縮まるのではないか？と推量する。
(4)　策3は、そもそも、"量子優位性"に繋がっていないと思われる。つまり、古典的にも、全く同じことができると思われる。
(5)　まとめると、次の通り：㊀古典的な｢グラフ･ランダムウォーク･トランスフォーマー(GRWformer)｣を構築できるだろう。㊁GQWformerとGRWformerは、精度の向上において、大きく変わらないのではないだろうか。

【0】はじめに
　東京大学^🐾1他^🐾2の研究者は、量子機械学習(QML：Quantum Machine Learning)の現状を整理した論文[*A-42](以下、本論文)を発表した(24年6月8日@arXiv)。なお、量子強化学習は、対象範囲外である。
　為念：データ科学アプリケーションあるいは実用的商用アプリケーションにおいて、古典的機械学習に代わりQMLの適用を検討する主な目的は、サンプル複雑性または時間複雑性のいずれかの点で、古典的機械学習を上回る量子優位性を実証することである。サンプル複雑性における優劣は、汎化性能を達成するための学習データ量の多寡である(少ない方が優れている)。計算複雑性における優劣は、計算速度が速いか遅いかである(速い方が優れている)。
🐾1　博士課程在学中で、インドからの留学生と思われる☞　https://www.kddi-foundation.or.jp/static/about/Business_Report_2023.pdf
🐾2　IBM東京基礎研究所及びJPモルガン(兼東京大学兼慶應義塾大学)。

【1】特定された調査の対象領域及びQMLフレームワーク
　本論文では、現実世界のシナリオに関連するアプリケーションと技術の探求を指向した結果、以下の3つの領域に焦点を当てている^🐾3：
❶　高エネルギー物理学(HEP：High Energy Physics)^🐾4　
❷　ヘルスケア　
❸　金融　
🐾3　量子化学については、次の様にコメントされている：量子化学は、QML が大きな可能性を秘めているもう 1 つの有望な分野であると認識している。しかし、量子化学とHEPにおけるQMLの応用は性質が似ており、どちらも複雑な量子システムをシミュレートしてその特性を理解することに主眼を置いているため、量子化学を除外することにした。
🐾4　残念ながら、現在の物理学は、エネルギー･スケールを超えた統一的な理論を構築出来ていない。 例えば、標準模型は電弱スケール(10²オーダーGeV)の低エネルギー有効理論に過ぎない。高エネルギー物理学は、文字通り、より高いエネルギー･スケールを扱う。極めて雑に言えば、強い相互作用や重力を含めた"大統一理論”を記述するのが、高エネルギー物理学である。

　QMLフレームワークとしては、以下2つを対象としている：
①　量子カーネル法　→量子特徴量ベースのアルゴリズム、とも表現される。
②　変分量子アルゴリズム　

【2】特定された調査の対象領域に対する短いコメント
❶　高エネルギー物理学(HEP)　
　㊀古典データを使って古典的機械学習で処理した結果と、㊁古典データを使って量子機械学習で処理した結果、を比べて、㊁が㊀より優れていると示すことは困難である(と広く認められるに至った)。一方で、㊂量子データを古典データに変換して、古典的機械学習で処理した結果と、㊃量子データを、そのまま量子機械学習で処理した結果を、比べて㊃が㊂より優れていると示すことは有望であると見做されてる。これは、R.P.ファインマンによるオリジナルの神託である｢君たちは、間違った物理を使っている！｣とも合致する。
　HEPに対するQMLは、㊃に相当する。調査対象領域としては、妥当というより鉄板であろう。
❷　ヘルスケア　
　ヘルスケアでは、予測の誤りが重大な影響を及ぼす。演算速度ではなく、精度(accuracy：正解率＝医療分野では正診率)が最も重要である。従って、計算複雑性は、それほど問題とはならない。その一方で、サンプル複雑性は、大きな意味を持つ。罹患者より健常者が圧倒的に多いので、疾患を示しているデータが圧倒的に少ないからである。希少疾患なら尚更である。もちろん、データ拡張の研究も行われているが、ヘルスケア(診断、検出)においてQMLへの期待は大きいと思われる。ただし、これまでのところ、芳しい成果は得られていない^【6】(1)。
　本論文では、9量子ビットより5量子ビットの性能が優れていた例が示されている。この理由は、｢学習や推論のランダム性により量子ハードウェアのパフォーマンスが不安定になり、古典モデルと同等のヘルスケア画像分類を実行できない｣と説明されている。現状(将来も？)、QMLをヘルスケアに適用することは難しいと言わざるを得ないだろう。
❸　金融　
　金融に適用可能な機械学習アプリケーションには、資産価格設定のための回帰、ポートフォリオ最適化のための分類、ポートフォリオ･リスク分析と銘柄選択のためのクラスタリング、不正検出のための特徴量抽出、アルゴリズム取引のための強化学習、リスク評価のための自然言語処理、財務予測、会計と監査など多岐に渡る。しかし、QMLが優位性を発揮したという明確な証拠は示されていない。

【3】QMLの活躍を制限している要因
　本論文は、掲題につき、以下を上げている(本論文には含まれているが、QML以外にも当てはまる一般的な話題は、本稿では除外している)。また、下記の順番(1)～(4)は、本論文において記述されている順番とは異なる。：
(1)　データローダー　
　まず、本論文は｢古典的なデータを量子状態として効率的にロードできるか？は、QMLアルゴリズムを使用した高速化を議論する研究で、しばしば無視されてきたボトルネックである｣と指摘する。本論文では、この障害の対応策として、 量子ランダムアクセスメモリ(QRAM)を提示している。しかし、QRAMは現実解とはならない可能性が高い(と思われる)。
　QRAMは、データ数Nの対数時間log(N)で、データロード(データ転送)が可能であると広く信じられている。ここで、物理量子ビット数をnとすると、N＝2ⁿであることは、お馴染みである。つまり、O(log(N))＝O(n)である。しかしQRAMは、"理論的にも”、実現の見通しが立っていない(つまり、実現の見通しが立たない根本的な理由は、エンジニアリング由来ではない)^🐾5。仮に、理論的に実現の見通しが立ったとしても、QRAMを実現するには多数の量子ゲートが必要と考えられているため、現実的ではない。
　そこで通常は、データ転送装置＝データローダーとして、パラメータ付き量子回路(PQC：Parametarized Quantum Circuit。しばしばアンザッツと呼ばれる)が想定される。PQCを使ったデータローダーは、多項式式時間poly(n)でデータ転送できると考えられている。
　データ転送装置＝データローダーと書くと、本質が分かり辛くなるので、改めてデータローダーの仕事を記述する。データローダーの役割は、｢古典的なデータが与えられた場合に、データを一度読み取り、適切な量子状態を表現する量子回路を出力すること｣である。
🐾5　QRAMを使ったとしても、多項式程度の加速しか得られない場合があるらしい[*A-43]。
❚為参考❚　確率ローディングについては、こちらを参照。

(2)　不毛な台地　
　本論文では、不毛な台地に対する、一般的な(広く知られている)回避策や軽減策が示されている。ただ、変分量子アルゴリズムに量子優位性はないだろう、と予想する論文[*A-44]が存在する。[*A-44]は、不毛な台地を回避できる問題は、多項式時間で古典的にシミュレート可能である(つまり、量子優位性はない)ことを見出した、と主張している。なお、量子畳み込みニューラルネットワーク(QCNN)は、不毛な台地が発生しないことが知られている。
　[*A-44]の予想が正しいとすると、量子カーネル法、QCNN以外のQMLには、そもそも量子優位性など存在しないことになる(CNNとカーネル法の関係は深い)。ちなみに、量子特徴量にしか"できなさそうな"機械学習タスクは存在するが、現実的なデータセットに関して量子優位性が示された例はない[*A-43]とされている。

(3)　ハードウェアの制限
　量子ハードウェアのノイズに対抗する一般的な戦略は、測定回数を増やすことである。しかし、これは測定中の読み出し誤差のために逆効果になる可能性もある。
　対応策としては、shot-frugalオプティマイザの使用が提示されている。shot-frugalオプティマイザでは、確率的勾配降下法に基づくアプローチを使用し、各反復で必要なショット数(測定数)を調整することで、良い塩梅を目指す。

(4)　実行時間が”長い”ーつまり、計算が”遅い！”　
　量子演算をエンドツーエンド、つまり状態準備から測定まで含めると、量子演算は『遅い』。本論文では、100 イベントに対して500 回の学習反復を実行するのに約 200 時間かかった例が上げられている。また、量子回路の実行時間は、総実行時間のわずかな割合(1％未満)を占めているに過ぎないことも示されている。
　対応策として、量子連合学習(QFL：Quantum Federated Learning)が提示されている。

【4】未解決の問題
(0)　QMLにおける量子優位性　
　本論文は、掲題について、以下のように整理している：
0⃣　量子アルゴリズムで観察されている量子優位性は、特定の状況下でのみ実現されている。
1⃣　観察された量子優位性が、慎重なハイパーパラメータの選択、ベンチマーク、および比較のみに起因するのか、それとも根本的な構造上の利点があるのかどうかは不明である(つまり、誇大宣伝の可能性がある)。
2⃣　分野としてのQMLは、｢経験科学｣になりつつある。例えば、量子優位性を”理論的に証明”することは困難になると予想されており、｢実用的なデモンストレーション｣に益々、重点が置かれている。この傾向は、量子ビット数と回路の深さが、｢100×100｣を超えると特に顕著になる。
3⃣　特定の学習問題に対して、量子学習アルゴリズムに匹敵する結果を達成できる、効率的な古典的アルゴリズムが存在する可能性がある。
4⃣　ヒューリスティックな量子学習アルゴリズムのどれもが、古典的に困難な学習問題を解決できることが証明されていない。
--------------------------------
　以下、本論文が考える、QMLにまつわる未解決課題をまとめた(＝問題提起)：
(0)　そもそも、量子優位性を議論するには、実用的なアプリケーションにとって興味深い問題と、古典的な方法でシミュレーションするのが本当に難しい問題の両方を特定することが重要である。これには、古典的な方法によって達成された進歩を認め、高いエンタングルメントを古典的なシミュレーションの難しさと単純に同一視しないことが必要である。
(1)　QMLアルゴリズムの量子優位性を効果的に評価するには、標準化されたベンチマークを確立することが重要である。ベンチマークを確立するには、簡単に準備できる量子状態が必要である。併せて、ベンチマークを行うためのオープンソースソフトウェアも必要である。
(2)　特定のデータセットに最適な量子符号化手法を見つける(入力問題あるいは、データ･ローディング問題を解決する)ことは、対処する必要があるもう 1 つの重要な課題である。
(3)　アンザッツ選択は、不毛な台地を防止し、効率的なスケーラビリティを実現する上で重要な役割を果たす。
(4)　アンザッツを使う場合、誤差逆伝播法は、古典回路に比べて大幅に効率が低くなる。誤差逆伝播法は、量子モデルに適した方法ではない可能性がある。
(5)　現在の QML にはプライバシー保護機能がないため、機械学習データセットで機密情報が漏洩する可能性があるという懸念が生じている。ただし、変分量子アルゴリズムは、古典アルゴリズムよりも敵対的攻撃に対して堅牢であるとされる。
(6)　説明可能なQMLは、未開拓のままである。
(7)　QML研究では、ハイパーパラメータの選択に関する広範な議論が不足しているため、透明性、解釈可能性等に課題が生じている。対処策として、研究者はハイパーパラメータの選択に関する詳細情報を含む包括的なドキュメントを提供することを優先する必要がある。

【5】考察
　24年末時点では、量子機械学習(QML)の実相が明確になってきていると言えるだろう。その実相を踏まえて提言するならば、日本産業社会におけるQML(とりあえず量子強化学習は除く)の研究開発は、次のように進めるべきではないだろうか(もちろん、当社の意見)。全方位にベットすることは、責任逃れに過ぎない。
㈠　まず、産業分野とアプリケーションを絞るべきである。ど真ん中は、あくまで製造業。ヘルスケアは避けた方が良い。金融は、常に微妙。アプリケーションでは、マーケティングやカスタマー･サービス等は、避けた方が良い。
㈡　その上で、｢ニューラルネットワークを使った深層学習のアウトプット｣より、｢カーネル法のアウトプット｣が優れているアプリケーションを抽出する。あるいは、｢畳み込みニューラルネットワーク(CNN)^🐾6のアウトプットが他のNNのアウトプット｣に比べて優れているアプリケーションを抽出する^🐾7。
㈢　もし、㈡のアプリケーションが見つからなければ、そこで終了。アプリケーションが見つかっても、当該アプリケーションで、将来にわたり金額的インパクトが小さいと予想されれば、そこで終了。つまり、公式のR&D費用は配分しない。
㈣　金額的インパクトが十分あると判断されれば、もしくは、金額インパクトが不明ならば、｢カーネル法→量子カーネル法｣あるいは、｢CNN→QCNN｣を検討する。
🐾6　なぜCNNかと言えば、不毛な台地が発生しないとされているからである。数理的な理由付けは、こちらを参照。
🐾7　つまり、トランスフォーマー、ボルツマン･マシン、再帰型ニューラルネットワーク、生成モデル等は除外されることになる。

(1)　24年話題になった例｜肝生検画像の二値分類タスク
　テラ･クオンタム(スイス)は、論文[*A-47](24年3月6日)にて、以下を主張している：量子特徴量を使った場合(量子モデル)は、古典特徴量を使った場合(古典モデル)に比べて、肝生検画像の二値分類タスクにおいて、精度(accuracy)が古典モデルより1.8％上回って、97.0％に達した。また、量子モデルの偽陰性率は5%未満であった。バックボーンモデルは、ResNet18。余談ながら、プライバシーの懸念に対応するため、連合学習を採用している。
　なお、学習データのサイズを(4400→1500と)縮小しても、量子モデルは精度がそれほど落ちない(97%→96%超)と主張しているが、古典モデルではサイズが減少して、むしろ精度が上がっている。そのため、｢学習データのサイズが縮小しても量子モデルの精度は。それほど落ちない｣という主張の信頼性は、やや怪しいと思われる。ちなみに[*A-43]には、｢現実的なデータセットに関して、量子特徴量を使って、量子優位性が示された例はない｣とある。

(2)　センサーデータにおける特徴量削減
‖概　要‖
　オーストラリア連邦科学産業研究機構の研究者は、論文[*A-48](25年1月23日)にて、以下を主張している(この論文は誤植がとても多い)：
　古典カーネル法ベースの主成分分析(cPCA)と量子カーネル法ベースの主成分分析(qPCA)を比較して、後者が｢控えめに優れている｣。化学抵抗性センサーアレイ(CSA)から得られたデータを使った。古典カーネルは、放射基底関数(RBF)カーネルである。量子カーネルは、パウリ特徴量マップ･カーネル^🐾8、ZZ特徴量マップ･カーネル及び自己適応量子カーネルである。特徴量削減後、CSAによって検出された化学物質の種類を予測することで、cPCAとqPCAの優劣を比較した。
　予測モデルは、ロジスティック回帰(LR)、線形カーネルSVM(L-SVM)、RBF-SVM、k近傍法(kNN)、ガウシアン･ナイーブ･ベイズ(NB)、ニューラルネットワーク(NN)、ランダムフォレスト(RF)、エクストラ･ツリー(ET)、GBC(Gradient Boosting Classifier)、XGB(eXtreme Gradient Boosting)。
　評価指標(スコア)は、正解率(accuracy)、F1スコア、コーエンの重み付きカッパ^🐾9が採用されている。
‖結　果‖
　実データを使った結果は、㊀データの次元^🐾10、㊁予測モデルに依存する。評価指標には、それほど依存していない。高次元(7次元及び6次元)✖｢kNN、NB、RF、ET、GBC、XGB｣では、qPCAとcPCAの性能は変わらない(qPCA≒cPCA)。GBCとXGBであれば、3次元までqPCA≒cPCAである。RBF-SVMとNNは、一貫してqPCA＞cPCAである。LRとL-SVMは、そもそもスコアが低いのでコメントの価値はないかもしれない。
‖結　論‖
　実データを使った結果に加えて、人工合成データを使った評価も行っている。併せた結論は以下の通りである。
❶　いくつかのケースで、qPCAの性能は、cPCAをわずかに上回った。
❷　qPCAが、全てのカーネルベースのcPCAよりも普遍的に優れていると判明したわけではない。
❸　非線形構造を持つデータセットに対して、qPCAは有用である。
‖為念：計算環境‖
　qPCAは、量子デバイス上で実行されたわけではなく、古典コンピュータ(Ryzen 5600G CPUと64Gbのメモリを搭載したコンピューター)上で行われた。つまりシミュレーション。
🐾8　本文中では、パウリZになっているが、図中ではパウリXになっている。
🐾9　医療分野では、二人の観察者間の診断の一致度を評価する指標として、カッパ係数が頻繁に使われる。順序尺度(軽症、中等症、重症)の診断一致度を調べる場合には、コーエンの重み付けカッパ係数を用いる方がより適切とされている。
🐾10　化学物質の種類と考えて良い。CSAは17個のセンサーで構成されているので、最大次元数は17。ただし、最大量子ビット数を7としたため、次元数は7までとしている。

(3)　量子古典ハイブリッド･モデル、LLM再学習の正解率を向上
╏概要╏
　米IonQ(量子H/W：トラップイオン)の研究者は、｢大規模言語モデルの再学習に、量子･古典ハイブリッド深層学習モデルを適用し、古典ベースライン比で正解率が向上した｣と発表した(25年4月11日@arXiv[*A-54])。少し正確に言うと、｢量子モジュールを分類ヘッドとして用いて、SetFitモデル^🐾11を再学習すると、正解率が向上する｣ことを示した。再学習手順において、事前学習済みモデルから重みを継承する古典層の上に、量子ヘッドを最終層として組み込んでいる。具体的な成果は2つに大別される➡以下①、②の通り^🐾12：
⓪　セットアップ　
　スタンフォード感情ツリーバンク(SST-2)^🐾13を使用した分類タスクを、ノイズ付き^🐾14状態ベクトルシミュレータ^🐾15で実行した。
①　成果1：正解率改善　
　量子古典ハイブリッド･モデル^🐾16は、古典ベースライン^🐾17よりも、高い正解率(accuracy)を達成することが示された。具体的には、最善の古典ベースライン(サポート･ベクター･マシン)に比べて、3.14%の改善を達成した。
②　成果2：スケーリング
1⃣　量子ビット数が増加するにつれて、正解率は上昇傾向を示す。☚重要なポイント！
2⃣　再アップロード回数、メインブロック層数、再アップロード層数の増加は、直接的に正解率を向上させるわけではない。
╏まとめ╏
　本ケースで｢量子＞古典｣を生み出した要因は、｢量子特徴量を使ったこと｣に由来する、と考えられる。
🐾11　SetFitは、Sentenceトランスフォーマーを用いて事前学習されたLLMである。対照学習に基づくSentenceトランスフォーマーの、少数ショットの再学習アプローチを導入している。Sentenceトランスフォーマーは、トランスフォーマー･ベースのモデルが利用できるPython のライブラリで、文章ベクトルを簡単に作成することができる。作成した文章ベクトルを利用することで、文章の分類や類似文章の検索といったタスクを、高い精度と効率で実行することが可能になる。
🐾12　ちなみに、消費電力は、1量子ビットあたり300Wと推定されている。超伝導方式の場合(24年時点で)、10W～50Wとされており、べらぼうに高い(持続可能ではないだろう)。100万量子ビットで300メガ･ワット(＝原発3基相当、≒ハイパースケール･データセンター3棟相当)。ちなみに、ハイパースケール･データセンター3棟⋍3,000～9,000億円。超伝導方式･100万量子ビット⋍1.5兆円程度とされる。トラップイオンは、9兆円程度になると言うことか？
🐾13　感情のアノテーションを付した感情分析に使える標準的なデータセット。
🐾14　脱分極ゲート･ノイズとショット･ノイズ(測定ノイズ)を考慮している。
🐾15　量子ビット数＝{10, 12, 14, 16, 18}
🐾16　為念：モデル･アーキテクチャは、ニューラルネットワーク。学習率は、量子ビット数(🐾15⤴)に応じて、{1.0, 1.5, 2.5, 3.0, 5.0}×10^-3。学習率の減衰なし。重み減衰なし。バッチサイズ16。
🐾17　古典ベースラインは、サポート･ベクター･マシン(RBFカーネル)、ロジスティック回帰、MLP(パーセプトロン)ベースのニューラルネットワークである。

❚概要❚
　デロイト･コンサルティング^🐾18他^🐾19は、薬物候補分子の生物活性(薬理活性)予測における、量子リザバー･コンピューティング(QRC)の性能を検証した(論文[*A-59](以下、本論文)発表は、25年8月5日)^🐾20。特徴量は、ほぼ量子特徴量で、"量子古典ハイブリッド方式"で計算されている。予測自体は、古典機械学習モデルで行う。なお、量子デバイスのモダリティは、中性原子。
🐾18　量子に前のめりである。QuEraと組むことが多い印象➡25年8月20日、提携を発表(⤵❚付録❚)。23年に、寺部雅能氏が移籍している(デンソー→住友商事→デロイト)。
🐾19　米QuEra(モダリティ：中性原子)、米アムジェン(バイオテクノロジー企業)、独メルク(大手製薬･化学品製造企業)。
🐾20　arXiv版[*A-60]は、24年12月9日。[*A-60]も本論文と呼ぶ。
❚方法論：量子古典ハイブリッド･カーネル法❚
1⃣　前説
　本論文では、勾配計算を使用しない。計算コストが高いからである。代わりに、本論文で、量子リザバー･コンピューティング(QRC)^🐾21と呼ぶ手法を使用する。もっとも、量子リザバー･コンピューティングと呼ぶよりも、”量子古典ハイブリッド”カーネル法^🐾22と呼んだ方が、肚落ちが良いと思われる。本論文及び[*A-61]の著者は、営利企業所属の研究者であるから、マーケティング的観点から｢新しい方法論を開発した｣と言いたい気持ちは理解できる。
🐾21　QRC自体は、[*A-61]において開発された。2値分類、多クラス分類、時系列予測などの機械学習タスクにおいて競争力のある性能を達成した、と主張。QRC向きのデータセットを探す必要性を指摘し、｢薬物候補の活性｣を候補として上げている。
🐾22　ただし、QRCと量子カーネル法が密接に関連していることは、[*A-61]でも指摘されている。
2⃣　量子古典ハイブリッド･カーネル法
　通常の量子カーネル法は、ヒルベルト空間において内積計算を行う。つまり量子回路を使って内積計算を行った後に測定を行う。量子古典ハイブリッド･カーネル法では、内積計算を量子回路で行わない。量子特徴量を測定して、実ベクトルとして取得する。この実ベクトルの内積をカーネルとする。つまり、ヒルベルト空間ではなく実ベクトル空間で内積を計算する。
　量子古典ハイブリッド方式の利点は、量子リソースが少なくて済むことである。ヒルベルト空間で計算した内積の測定には、複雑な量子回路が必要になる(ただし、その回避策がないわけではない)。
3⃣　補足　
　量子特徴量は、入力データに依存したハミルトニアンを使ったユニタリ時間発展演算子で、時間発展させられる。測定は、時間発展のタイムステップ毎に行われる。なお、時間発展が、量子特徴量に対する非線形変換になっている(☞❚考察❚3⃣)。
❚データセット❚
　Merck Molecular Activity Challenge(メルク分子活性チャレンジ：MMAC)^🐾23で使われた15個のデータセットから5つを選択して用いた。MMACデータセットには、治療標的に対する生物活性測定値が含まれている。
🐾23　MMACは2012年に、Kaggleが主催したオンライン･データサイエンス･コンテスト。参加者は約50,000の分子に対して事前計算された分子記述子を使用し、生物活性を予測する課題に挑んだ。2012年は、ジェフリー･ヒントン他が開発したAlexNetが画像認識タスクで衝撃を与えた年(深層学習元年?)でもある。
❚量子と古典の比較結果❚
1⃣　前説　
　量子古典ハイブリッド･カーネル法による薬理活性予測結果を、古典カーネル法の結果と比較する。量子×古典の比較であるが、速度は競わない(競えない)。あくまで精度を競う。
2⃣　諸々セットアップ　
　古典カーネル法では、RBFカーネルを採用した(色々端折っているが、下記3⃣⃣の結果はRBFカーネルを使用)。予測モデルは、サポートベクターマシン(SVM)を採用(色々端折っているが、下記3⃣の結果はSVMを使用)。下記3⃣に用いたデータセットは、MMACデータセットの中で、最も小規模なデータセット4である。さらに、クラスタリング･ベースのサンプリングを用いて、❶～❸の部分サンプルを作成した(ここでも色々端折っているが、下記3⃣では、そういう理解で良い)：❶小規模データ(100レコード)、❷中規模データ(200レコード)、❸大規模データ(800レコード)。
　なお、MMACデータセットは2値分類タスク用に変換されて(使用されて)いる。評価指標は、正解率(accuracy)、適合率(precision)、再現率(recall)、F1スコアの4つである。下記3⃣では、❶{正解率、適合率、再現率、F1スコア}のように表記する。また、”差異”は量子の値ー古典の値、である。
3⃣⃣　結果　
　量子❶{0.747、0.766、0.707、0.734}、❷{0.760、 0.776、0.747、0.752}、❸{0.742、0.763、0.713、0.734}
　古典❶{0.660、0.672、0.653、0.660}、❷{0.737、 0.784、0.680、0.716}、❸{0.709、0.727、0.689、0.702}
　差異❶{0.087、0.094、0.054、0.074}、❷{0.023、-0.008、0.067、0.036}、❸{0.033、0.036、0.024、0.032}
　❷の適合率を除いて、量子＞古典である！ 加えて、本論文が粒立てている主張は❶＞❷＞❸である^🐾24。言葉で表現すると、小規模データの方が、量子の利点("優位性")が大きいことを意味している^🐾25。この点につき本論文では、｢大規模データセットの整備が困難な医療分野では貴重である｣と主張している。
🐾24　本論文でそのような計算はなされていないし、統計学的な意味もないが、√(正解率²＋適合率²＋再現率²＋F1スコア²)を計算すると、次の通り：❶0.157、❷0.080、❸0.063。
🐾25　教科書的には、古典機械学習は小規模データでは過学習を起こし易く、汎化性能が低いと書かれている。
❚考察❚
1⃣　ガウス過程のような標準的な古典カーネル法は、特徴量空間を｢確率分布を使った確率ベース｣で最適解を探索している^🐾26と表現できる。本論文でQRC(本稿で量子古典ハイブリッド･カーネル法)と呼んでいる量子カーネル法は、特徴量空間をユニタリ時間発展(量子ダイナミクスを使った確率ベース)で探索しているということであろう。この場合、効率的に最適解を探索する鍵は、ハミルトニアンの設計が握っていることになる(はず)。
🐾26　二値分類に伴う誤差を最小化するようなカーネルを探索している、といった方が丁寧であろう。
2⃣　一言でまとめると、Viva量子特徴量・Viva量子カーネル法、であろうか。古典機械学習に対して何らかの優位性をもたらす量子機械学習は、量子特徴量を使った量子カーネル法であることは、ほぼコンセンサスであろう。また、何らかの優位性は速度ではなく、｢(ザックリした意味での)精度、少ない学習可能パラメータ数、少ない学習データ｣というところに収束していると思われる。
3⃣　特徴量の更新＝カーネルの更新における(QRCの)ユニタリ時間発展は、(古典)特徴量の非線形変換に相当するということは、ニューラルネットワーク(NN)的に特徴量の更新を行っているということになる。そうすると結局、NNをしっかりチューニングすれば、QRC(量子カーネル法)とNNの精度は同程度になるのではないか。という疑問が湧く。それは、おそらく真であろう。そこで、｢データ規模が小さい方が精度高いなんて、量子ならでは、ですよ!｣と主張したいのであろう。本当にそうであれば、(世間のイメージとは異なるものの)優位性が発現していると言って良いだろう。
❚付録❚
　QuEraとデロイトは25年8月20日提携を発表(https://www.quera.com/press-releases/quera-computing-and-deloitte-form-alliance-to-accelerate-enterprise-adoption-of-neutral-atom-quantum-computing)。
　提携の目的は、｢量子に関する意識向上、専門的な量子人材の育成、学術機関との共同研究、ユースケースの共同創出、量子スタートアップの支援｣らしい。

❚概要❚
　(米サンフランシスコに本社を置く新興企業という体である)不思議な組織Haiquは、自社公式ブログ[*A-76]で、以下のようなセンセーショナルな主張を行った(25年11月13日)：NISQ実機かつエンドツーエンドで、量子優位性有用性^🐾27を実現した。優位性有用性は、精度に加えて速度で実現した(☞❚考察❚2⃣)、とする。ポイントは、小規模と思われる(☞❚考察❚1⃣)。
🐾27　量子優位性は、｢超2次加速｣＋｢問題のスケールが大規模｣という状況で使いましょう、というトレンドに従う。量子的な手法を使うことで古典的な手法を使うよりも、｢何かしら良い結果｣が生じるという意味で、量子有用性を使う。
❚セットアップ❚
　アプリケーション対象は、異常検知^🐾28である。データは、異常値を含む多変量時系列データ。この古典データを、㊀パラメータ化量子回路に入力して量子特徴量を生成→量子特徴量を測定して、古典特徴量を生成→古典機械学習モデルに入力→2値分類する。比較対象は、以下：㊁古典的に古典特徴量を生成→同じ古典機械学習モデルに入力→2値分類する。
　F1スコアで比較して『概ね』、㊀＞㊁であった(☞❚詳しい結果❚を参照)。この、量子生成･古典特徴量×古典機械学習で(も)量子優位性有用性が現れるという主張は、グーグルの主張と同じ。学習プロセスではなく推論プロセスでのみ、量子優位性有用性が現れるというグーグルの主張と、少なくとも矛盾はない。なお、量子回路で量子特徴量を生成した後、測定して、古典特徴量を得るというアプローチをカッコよく呼ぶと、射影量子カーネル法、ということになるらしい。
🐾28　産業応用のイメージで言うと、堕天使(債券の非投資適格への転落)予測、倒産予測、金融不正取引･マネーロンダリングの検知、サイバー攻撃･情報漏洩の検知、製造業における不良品検出(☞下記(6)を参照)、インフラ故障の検知･予測、疾患の診断など、多岐に渡る。
❚Haiqu独自の差別的な技術要素❚
　兎にも角にも、新しい符号化手法である。
　古典データを量子データに符号化するために、既存の多くの研究では、角度符号化が多く用いられている。しかし、現実世界のデータセットには数百、数千の特徴量が含まれることがあるため、角度符号化では対応できない(とHaiquは主張)。そこで、同じ物理量子ビット数に対して、角度符号化比で多項式的に多くの特徴量を符号化できる新しい符号化手法を開発した、とする。
　なおHaiquは、従前にも、古典データを効率的に符号化する手法を提案している(英大手商業銀行HSBCと共同研究)。こちらを参照。
❚特徴量の生成❚
　506個の古典特徴量を持つ高次元ベクトルが生成された。
㈠　量子特徴量の生成・・・ランダムに選択されたパラメータを持つ量子回路の下で時間発展させ、その結果得られる量子状態を測定する^🐾29ことで、古典特徴量を生成する。量子回路の実装に使われたH/Wは、NISQ実機^🐾30及び、ノイズ無し量子シミュレータの2種類。NISQ実機では、128物理量子ビットを使用している。
🐾29　ショット数1,024　
🐾30　IBM Quantum Heronプロセッサ。物理量子ビット数は156。　
㈡　古典特徴量の生成・・・ランダム･ニューラルネットワークとランダム･フーリエ特徴量を使用して、古典特徴量を生成する。
❚古典機械学習モデル❚
　2値分類に使われた古典機械学習モデル^🐾31は、以下の5種類：❶決定木、❷勾配ブースティング、❸ロジスティック回帰、➍ランダム･フォレスト、❺サポート･ベクター･マシン(SVM)
🐾31　各モデルのハイパーパラメータは、個別に最適化された。また、データは学習：テスト＝80:20で分割された。
❚詳しい結果❚
　❶～❺について、{㊀のF1スコア、㊁のF1スコア}を示すと、以下の通り。ただし、この場合の㊀は、NISQ実機を使って量子特徴量を生成したケースである。
　❶{0.95,0.90}、❷{0.91,0.91}、❸{0.96,0.92}、➍{0.95^🐾32,0.90}、❺{0.80,0.91}。❶･❸･➍は、㊀＞㊁である→ツリー･ベースのモデルが良い結果を示した。❷は同スコア、❺は惨敗である。
　なお❸は、ノイズなし量子シミュレータを使って量子特徴量を生成したケースも示されている。その場合のF1スコアは0.98である。つまり、量子誤り訂正が施された量子H/Wであれば、その程度が期待できる(というデモンストレーション)。
🐾32　ママ。ただし、グラフでみると0.98くらいはあるので、おそらく誤植であろう(0.95は誤で、0.98程度が正か)。
❚考察❚
1⃣　Haiquによる本結果のポイントは｢小規模｣であると思われる^{🐾33,🐾34}。一般に量子優位性は、適当なしきい値を超える大規模スケールで現れる、とされる。しかし、実社会の古典データを使った量子機械学習分野では、データ･ローディング問題のため、量子優位性は消えるとされる。それが、問題のスケールが大規模であっても高々、多項式オーバーヘッドで状態準備が可能と信じられている、量子シミュレーションとの違いである。
🐾33　小規模⇔推論、というわけではない。とは言え、本研究の結果は、NISQでも推論であれば量子有用性が示せる、との傍証にはなるだろう。
🐾34　どの規模まで、Haiquの結果が適用できるのかは興味深い。
2⃣　小規模でデータ･ローディング問題を回避していると思われるため、速度における優位性有用性は、僅かであろう(定量的には、示されていない)。とはいえ、｢機械学習の分野且つエンドツーエンド且つNISQ実機｣という座組で、量子が(たとえ僅かでも)速いという主張は、これが初めてであろう。重要なマイルストーンが達成された、と言って良いのではないだろうか。

❚はじめに❚　
　慶應義塾大学とTOPPANホールディングスは、量子カーネル･ベースのサポート･ベクター･マシン(以下、量子カーネルSVM)を使った｢長距離でも高い正解率を維持する異常検知システムを開発した｣と発表した(25年9月8日)[*A-96]。成果は、量子コンピューティングの国際会議QCE25にて発表された(日本時間9月6日)。arXivにて成果が論文[*A-97](以下、本論文)として一般公開されたのは、10月7日であった。
❚概　要❚
　前述の通り、アプリケーションは異常検知である。このアプリケーションは、上記(5)と同じである。異常は稀にしか発生しないので、異常データは量が少ない。当該状況では、古典機械学習モデルに比べて量子機械学習モデルの方が、高性能であると考えられている。そして、識別能力が高く・非線形空間を効果的に分離できる機械学習モデルとして、カーネル･ベースのSVMが、本論文では採用されている。
　斯様な事情のため本論文は、ある意味でTEPPANケースを扱っていると言える。
❚本論文の主張❚　
　本論文は(本論文の設定で)、以下を主張する(☞設定については、❚セットアップ❚を参照)：
㈠　量子カーネルSVMは、ノイズや距離による信号劣化に対して、堅牢である。
➡　量子カーネルSVMは、古典カーネルSVMよりも、遠くにある異常の存在を正確に検出できる(☞❚比較結果❚㈠)。
㈡　効果サイズ分析(☞❚効果サイズ分析：コーエンのd❚)により、量子カーネルSVMと古典カーネルSVMとの差は明確である(☞❚比較結果❚㈡)。
㈢　量子カーネルSVMは、複数の種類の異常を明確に区別できる(☞❚比較結果❚㈢)。
❚効果サイズ分析：コーエンのd❚　
　2群の比較において、統計的有意差を補足するために、導入される統計量の一つ。しきい値(基準値)に曖昧さが残る＋定量的な比較ができないため、｢統計的有意差･統計的有意性｣は、ある意味いい加減である。そこで、様々な補完的な統計量が導入されるが、コーエンのdも、その一つである。d＝(2群の平均値の差)/2群で平均した標準偏差、で定義される。
　d > 0.8で効果大＝明確な差がある、とされる。ただ、どこまで行っても、曖昧さは残る。
❚セットアップ❚
㈠　概要　
　ノイズの多い工場環境において、異常を検知する1クラス分類タスクを実施した。1クラスとは、1つのクラスのデータのみを使って学習することを指す。本論文の場合で言うと、正常データのみを使って学習している。
　量子カーネルSVMは、NISQ実機ではなく、IBMの量子シミュレータを使って実行された。古典カーネルSVMは、カーネルにRBF(動径基底関数)カーネルを採用している^🐾35。2つのSVMを比較する指標には、正解率(accuracy)とF1スコアを使用した。
🐾35　RBFカーネルのパラメータは、交差検証によって最適化された。
㈡　ハードウェアのセットアップと特徴量　
　コンベアとチェーンベルト･マシンに、非接触センサーとして、指向性マイクをさまざまな距離で配置し、音響信号を収集･取得した。さまざまな距離を具体的に述べると、{0,1,2,3m}である。音声データは、自己回帰モデルを用いて処理され^🐾36、古典特徴量が生成された。古典特徴量は、量子カーネルを介して量子特徴量空間にマッピングされる(量子特徴量が生成される)。古典並びに、量子機械学習モデルに使われた特徴量の数は、5つ^🐾37である。
🐾36　自己回帰モデルのパラメータが古典特徴量となる。このパラメータを推定することは、Yule-Walker⽅程式と呼ばれる方程式を解くことに帰着(変換)できる。Yule-Walker⽅程式は、Levinsonアルゴリズム(Levinson-Durbin再帰アルゴリズム)を使うことで、効率的に解けることが知られている。本論文も、Levinsonアルゴリズムを使って、パラメータ推定(＝古典特徴量の生成)を行っている。
🐾37　赤池情報量基準(AIC)とベイズ情報量基準(BIC)を調べた予備実験に基づき、5つに決定された。
㈢　データセット　
　60個の正常/正常、30個の異常/異常、30個の異常/正常、60個の正常/異常という包括的なデータセットを構築した。ここで、正常/正常とは、コンベアとチェーンベルト･マシンが共に正常に動作したことを表している。40個の正常/正常データを学習データとして用い、残りをテスト･データとして使用した。
　異常データは、装置に釘を挿入することで発生させた異音データである。
❚比較結果❚
㈠　正解率とF1スコアの比較
　量子カーネルSVMは、距離が離れて(0→3m)も、正解率とF1スコアが大きく低下しない^🐾38。それどころか、3mでも正解率＝1かつF1スコア=1である。1mでは正解率≒0.95、F1スコア≒0.92とやや低下する。2mでの結果は定量的に示されていないが、1mの結果より改善している。この1mと2mの位置での低下は、音響干渉パターンによるものと説明されている。
　一方、古典カーネルSVMは、距離が離れると、正解率及びF1スコアが大きく低下する。2mで急低下し、3mでは上昇する。2mの正解率は、{チャネル1、チャネル2、チャネル3}^🐾39の順で、{0.46、0.27、0.41}、F1スコアは{0.46、0.22、0.42}である。
　結論としてまとめると、量子カーネルSVMは古典カーネルSVMに比べて、遠くにある異常の存在を正確に検出できる。
🐾38　チャネル(⤵)の違いは、ほぼない。
🐾39　チャネル1とは、｢0mにチェーンベルト･マシンのみの音響信号を取得するマイクを設置し、他の1,2,3mは両方の装置に対し、マイクを設置する｣というセットアップ。チャネル2は、全距離で両方の装置に対しマイクを設置。チャネル3は、0mがコンベアのみ。
㈡　効果サイズ分析
　コーエンの dを使用した効果サイズ分析で、d > 1.4となった。この値は、2群間の明らかな違いを表すしきい値0.8を大幅に上回った。これは、量子カーネルSVMが古典カーネルSVMよりも約 1.5 標準偏差優れたパフォーマンスを発揮することを示している。
　ただし、サンプル サイズが限られている(距離は、0,1,2,3mの4種類である)こと及び、制御された実験条件を考えると、これらの効果サイズは慎重に解釈する必要がある(と本論文は結ぶ)。
㈢　複数種類の異常を区別可能
　量子カーネルSVMを用いた場合、説明能力が高い2つの特徴量が存在した。この2つの特徴量で作った2次元特徴量空間において、異常点の可視化を行った。その結果、量子カーネルSVMは、特徴量空間における特徴的なパターンに基づいて、複数種類の異常を区別できることを示された。
❚量子カーネルSVMが高性能であることを説明する要因❚
①　指数関数的な特徴空間次元
　量子特徴量マップは、古典特徴量を32次元の量子ヒルベルト空間に射影する。これにより、古典RBFカーネルと比較して、決定境界構築の自由度が指数的に向上する。
②　エンタングルメントで強化された分離可能性　
　量子回路におけるエンタングルメント演算は、特徴量間の新たな相関関係を作成し、ノイズ下でも微細な識別を可能にする。
③　ノイズ耐性のある量子状態　
　量子重ね合わせは複数の古典状態を同時に符号化することを可能にし、古典手法には欠けている固有の冗長性をもたらす可能性がある。
❚為参考：制限❚　
㈠　雑音　
　背景雑音が信号の85%を超えると、性能低下が観測された。
㈡　飽和　
　特徴量数が8を超えると、量子カーネル法の性能は頭打ちとなった。これは、量子回路の表現力に限界があることを示唆している。
㈢　干渉　
　5つ以上の音源が同時に存在する環境では、指向性マイクの選択性が低下し、古典カーネル法と量子カーネル法の両方に影響を与えた。
❚考察❚　
㈠　量子カーネルベースの機械学習モデル✖異常検知は、TEPPANネタではある。ただ、製造業(ノイズ環境下にある工場内の装置)に対して問題設定した、という意味で、目の付け所が良い、という評価は出来るだろう。そして、結果は素晴らしいものの、量子カーネル法と古典カーネル法で、本当にここまでの差が出るものなのだろうか。
㈡　量子カーネルSVMは、初期学習プロセスにおいて正常な状態を異常と分類することがあるものの、❚比較結果❚㈠で示したように、異常を見逃すことはほとんどない。一方、同じく❚比較結果❚㈠で示したように、古典カーネルSVMは多くの異常を見逃している。製造業においては、偽陽性は偽陰性よりもはるかに大きな懸念事項である。その観点からも、量子カーネルSVMは望ましい、本論文は結論している。

❚概　要❚　
　九州大学･BlueMeme^🐾1･京都大学は、｢転写因子(TF)^🐾2の結合部位(TFBS)予測において、量子古典ハイブリッド機械学習モデルが古典機械学習モデルより優れていることを確認した｣という論文(以下、本論文[*A-99])を発表した(@Briefings in Bioinformatics^🐾3、25年11月26日)。本論文で提示されている量子古典ハイブリッド機械学習モデルは、QTFPredと呼ばれている。
　量子機械学習目線で本論文の結果を端的に述べると、データが限られた(疎データの)状況で、QTFPredは古典機械学習モデルよりも優れている、という内容である。なお、モデル･アーキテクチャは、畳み込みニューラルネットワーク(CNN)である^🐾4。
🐾1　事業内容が｢ローコード技術とアジャイル手法を中心としたDX事業｣である新興企業。出所は、該社サイト(https://www.bluememe.jp/company/)。
🐾2　Transcription Factor。DNAに結合することで、遺伝子の発現を制御するタンパク質。
🐾3　英オックスフォード大学出版局が発行する、生命科学分野の査読付き国際学術誌。特にバイオ･インフォマティクスにおける最新の手法や応用研究を扱っているらしい。
🐾4　これまでの量子アプローチによるTFBS予測は、量子アニーラを用いた2次制約無し二値最適化(QUBO)により行われてきた。しかし、同アプローチには、以下のような制約があり、不十分なアプローチとなっていた：㊀量子アニーリング･プラットフォームの制約。㊁データからではなく、QUBO関数によって事前に決定された、静的な特徴量表現から学習する。㊂処理可能なDNA配列長が約10 bp(塩基対)しかない。㊃TFの範囲が狭い(4種類のみ)。
‖為参考：概要の補足‖　
　本論文の内容は分子生物学･生化学への踏み込みが深いが、本稿は、あくまで量子機械学習目線で整理する(ので、本論文の｢分子生物学･生化学｣的主張を全て拾っていないので注意)。ただし、本論文は量子機械学習の文脈で、目新しい技術が使われているわけではない。誤解を恐れずに言うと本論文の内容は、量子古典ハイブリッド機械学習を分子生物学･生化学に適用して、古典機械学習より良い結果を得た、という内容である。
❚本論文の主張❚　
　TFBS予測において、TFBS二値分類と結合シグナル回帰(☞❚タスクの整理❚)を実行して、量子古典ハイブリッド･モデルが古典モデルより優れていることを定量的に確認した(☞❚比較結果❚〖1〗㈡及び〖2〗㈡)。比較に用いた指標は、IOUスコアとピアソン相関係数である。優れているの意味についは、❚考察❚も参照。
❚量子技術の概要❚　
　本論文における量子古典ハイブリッド機械学習モデル^🐾5のアーキテクチャは、古典CNNにおける最初の畳み込み層を、量子回路で置き換えたというものである。量子回路で置き換えられた最初の畳み込み層＝量子畳み込み層では、量子回路学習^🐾6が実行される。
　本質に根ざした目線かつ機械学習モデル目線でいうと、QTFPredは『古典』機械学習モデル(具体的には、CNN)である。通常の古典機械学習モデルとの違いは、特徴量のみにある。(古典)特徴量は、量子回路･量子特徴量経由で生成されている。そのことを踏まえた上で、量子回路学習(Quantum Circuit Learning：QCL)で実行されるフローを示すと、以下の通り：古典特徴量^🐾7→量子状態に符号化^🐾8→パラメータ付き量子回路(アンザッツ)でユニタリ変換→計算基底で測定(期待値計算)して、新しい古典特徴量を生成→新しい古典特徴量を、古典CNNにおける後続の層への入力として使用する^🐾9,🐾10。
🐾5　学習モデル諸元：量子回路学習→オプティマイザーはAdamW。初期化アルゴリズムはXavier法。最大学習エポックは40。早期停止あり(patienceは6エポック)。╏ CNN→スキップ接続が導入されている。損失関数は、TFBS二値分類が、ハード･ネガティブ･マイニング損失。結合シグナル回帰は、二乗平均平方根誤差。
🐾6　｢QunaSys≒大阪大学･御手洗光祐准教授｣グループが開発した、変分量子アルゴリズム。量子回路学習と量子カーネル法は、｢量子特徴量ベースのアルゴリズム｣として、カテゴライズされている。つまり、量子カーネル法の親戚という理解で良い。
🐾7　DNA配列をワンホット符号化し、TF結合に関連する局所的な配列特徴量を抽出している。
🐾8　まさに定番とも言える｢角度符号化｣を用いて、量子状態に量子符号化している。
🐾9　射影量子カーネル法：｢古典特徴量→量子特徴量→新しい古典特徴量｣✖古典機械学習モデルで、量子有用性を捻り出す、というのが、2025年時点における量子機械学習のトレンドである。上記(5)及び(6)も同じ座組。
🐾10　QCLベースの量子機械学習を採用したことにより、量子アニーリング･アプローチによる制約(☞🐾4)から逃れて、より長い配列(1000bp、←㊂対策)と多様なTF(←㊃対策)にわたるTFBS予測が可能になった、とする。
‖為参考扱い：量子技術等の補足‖　
❑　本論文は、NISQ実機ではなく、量子シミュレータを使っている。
❑　塩基対(bp)のサイズは16である。このサイズは、ほとんどの TF 結合モチーフを包含する。JASPAR2024 モチーフの 96.5% は 16 bp 以下である。JASPARとは、ノルウェーやデンマークを中心とした研究グループが開発・運用している、TFの結合予測配列に関するオープンアクセスDBらしい。
❑　16 量子ビットの量子回路をシミュレートすることは計算上法外である(本論文ママ)ため、カーネル分割戦略を採用した。カーネル分割戦略とは、16bpを4量子ビット(2⁴＝16)のアンザッツに分割することを指している。
❚事前知識の整理❚　
㈠　TFBS予測とは？　
　転写因子(TF)は、転写因子結合部位(Transcription Factor Binding Sites：TFBS)と呼ばれる特定のゲノム配列モチーフ^🐾11に結合することで遺伝子発現を制御する。TFBSを正確に予測することは、遺伝子制御メカニズムとその発達及び、疾患への影響を理解する上で不可欠である。
🐾11　タンパク質アミノ酸配列には、その機能と密接な関係がある特徴的な配列パターンが存在する。この特徴的な配列パターンをモチーフと呼ぶ。タンパク質アミノ酸配列におけるモチーフは、遺伝子配列にも保存されていると考えられている。これをゲノム配列モチーフと呼ぶ。
㈡　TFBS予測モデル　
　TFBS予測を実験的に行うことは高コストであるため、一般的には計算的手法が代替え的に行われてきた。具体的には、位置重み行列に代表される確率モデルやサポート･ベクター･マシン(SVM)に代表される機械学習モデルが使われてきた。深層学習モデルの進歩に伴い、FCN(完全畳み込みニューラルネットワーク)^🐾12やCNNがTFBS予測にも導入されるに至った。 本論文では、古典CNNを一部量子化したモデルをTFBS予測に適用する。
🐾12　線形層が全て畳み込み層だけで構成されているCNN。
❚タスクの整理❚　
　本論文において、QTFPredと古典機械学習モデルの比較検証に用いられたタスクは、❶TFBS二値分類と❷結合シグナル回帰、の2つである。❶TFBS二値分類とは、TFBSにTFが結合する(この場合、値1)か、結合しない(同値0)かの二値に分類するという分類タスクである。500bpのDNA配列中の各塩基について、値1と値0を区別する。なお、❶の古典参照モデルはFCNとFCNA^🐾13である。
　本論文で言う❷結合シグナル回帰とは、1000bpの配列全体にわたるChIP-seq^🐾14データから結合シグナルの回帰性能^🐾15を評価するタスクである。端的に言うと、TFBSをゲノム配列上でピンポイントに特定するというタスクである。❶と同種であるが、”より複雑なタスク”であり、実数値の強度キャプチャ、連続ラベルにおけるノイズ処理、そしてより長い配列を高次元出力空間で処理する必要がある。❷の古典参照モデルは、BPNet 及びFCNsignal^🐾16である。
🐾13　FCNAは、FCN(☞🐾12)とグローバル平均プーリングを用いてChIP-seqデータ(⤵🐾14)から、TFBSとモチーフを予測するモデルである。
🐾14　ChIP-seq(全ゲノムクロマチン免疫沈降シークエンス)は、クロマチン免疫沈降法(Chromatin Immuno－Precipitation：ChIP)で得られたDNA分画をシーケンス(Sequencing:seq)することで、TFBS(やヒストンの翻訳後修飾など)をゲノムワイドに同定するための強力な実験的手法。
🐾15　ChIP-seqの結果をゲノム座標を横軸にプロットすると、TFBSを示す座標では、ピーク値を示す。このピーク値の検出が｢結合シグナル回帰｣と呼ばれている(と理解)。回帰(regression)という文言がピンと来ない。
🐾16　BPNet は、膨張(あるいは拡張)畳み込み層を使ったCNN モデル。膨張畳み込み層とは、カーネルの走査位置を膨張させることにより少数の層のみで、効率的に広い受容野を確保できる畳み込み層らしい。
　FCNsignalはFCNAに似た構造をしているが、グローバル平均プーリングの前に、ゲート付き回帰型ユニット(GRU)が追加されている点が異なる。GRUの追加は、配列特異的特徴量の長期依存性を捉えることを目的としている。
❚比較結果❚　
〖0〗学習及びテスト用のデータセット　
　9のEncyclopedia of DNA elements(ENCODE) ChIP-seqデータセットを用いる。ENCODEは、米国立ヒトゲノム研究所(NHGRI)が2003年に立ち上げたヒトゲノム解析プロジェクト。ヒトゲノムのすべての機能要素の解析を目指している。世界五ヶ国(日米英西シンガポール)から32研究機関が参加している。
〖1〗TFBS二値分類予測タスク　
㈠　概略　
　3つのヒト細胞株^🐾17、49個のTFを対象とした、TFBS二値分類予測タスクである。比較指標は、IOUスコア(ジャカード指数とも呼ばれる)である^🐾18。IOUスコアは、二値分類モデルの性能評価指標の一つであり、データセット間の類似度･重なり具合を測るために使用される。本論文の場合、予測されたTF領域と実験的に得られているTF領域(＝グランドトルゥース)との重なり具合を測っている。
🐾17　壱：ヒト肺由来上皮細胞株(A549：15個のTF)。弐：ヒト血液由来Bリンパ芽球様細胞株(GM12878：20個のTF)。参：ヒト乳房由来上皮細胞株(MCF7：14個のTF)。
🐾18　堅牢な性能評価を確実にするために、タスクは、10回の独立した試行にわたって実施された。そのため、IOUスコアも平均IOUスコアであるが、簡便さを優先し、単なるIOUスコアと表記した。以下、同じ。
㈡　IOUスコア比較　
　MCF7(☞🐾17の参)に対するIOUスコアを、本論文では2例^🐾19で数値が示されている。具体的には、{0.77、0.66、0.58}と{0.87、0.86、0.75}である。ここで、数値は{QTFPred、FCNA、FCN}の順で示した(以下、同じ)。本論文は、QTFPred は49(15＋20＋14、☞🐾17)個のTF中、45個(45/49≒91.84%)で古典参照モデルを上回ったと主張する。
🐾19　低ピークと高ピーク群の例。具体的には、TAF1(4093ピーク)＝{0.77、0.66、0.58}とCTCF(44480ピーク)＝{0.87、0.86、0.75}。
㈢　標準偏差による安定性分析
　結論は、特に限られたデータで堅牢性･安定性を示した、である。まず、TFを⓵低ピーク群(⁠≦ 10,000)、⓶中ピーク群(> 10,000～ ≦ 20,000)、⓷高ピーク群(> 20,000)の3群に分別した。低ピーク群のデータは、(異常値データなどと同じ)疎データと考えて良い。MCF7に対するIOUは、⓵{0.75、0.68、0.64}、⓶{0.77、0.71、0.66}、⓷{0.79、0.74、0.68}という結果であった。定性的な傾向(QTFPred＞FCNA＞FCNという順序)は、A549及びGM12878でも同様であった(詳細は割愛)。
　MCF7 に対する標準偏差は、⓵{0.022、0.057、0.049}、⓶{0.041、0.073、0.067}、⓷{0.050、0.085、0.073}であった。標準偏差においても、定性的な傾向(QTFPred＞FCNA＞FCNという順序)は、A549及びGM12878で同様であった。この標準偏差の比較から、QTFPredは古典参照モデルに比べて、堅牢性･安定性を示したという評価を下している。特に、低ピーク及び中ピーク群＝限られたデータで、安定している(かつIOUスコアも高い)ことが高く評価されている。なぜなら、ENCODE ChIP-seqデータセットの45.6%が低ピーク群に、69.2%が低ピーク＋中ピーク群に該当するからである。
〖2〗結合シグナル予測タスク　
㈠　概略　
　3つのヒト細胞株^🐾20、49個のTFを対象とした、結合シグナル予測タスク である。比較指標は、ピアソン相関係数である。ピアソン相関係数は、2変数間における線形相関の程度を表す指標であり、－1～1の範囲で値をとる。本論文では、予測された結合シグナルと実験的に観測されている結合シグナル(＝グランドトルゥース)とのピアソン相関(スコア)を用いた。
🐾20　壱：ヒト子宮頸癌細胞株(HeLa-S3：12個のTF)。弐：ヒト血液由来慢性骨髄性白血病細胞株(K562：17個のTF)。参：ヒト血液由来Bリンパ芽球性細胞株(GM12878：20個のTF)。　
㈡　ピアソン相関係数比較　
　HeLa-S3に対して、 データセットをピーク･サイズに基づいて3群(⓵低、⓶中、⓷高)に分け、ピアソン相関係数を比較した。{QTFPred、FCNsignal、BPNet}の順で数値を示すと、⓵{0.70、0.61、0.36}、⓶{0.75、0.69、0.49}、⓷{0.78、0.74、0.60}であった。QTFPredは高いピアソン相関係数を達成している。本論文は、QTFPred は49(12＋17＋20、☞🐾20)個のTF中、48個(48/49≒97.96%)で古典参照モデルを上回ったと主張する。
㈢　標準偏差による安定性分析
　標準偏差は、 ⓵{0.068、0.14、0.089}、⓶{0.075、0.14、0.15}、⓷{0.081、0.12、0.18}であった。この傾向は、K562とGM12878でも同様であった(詳細は割愛)。標準偏差の比較から(TFBS二値分類予測タスクと同じように)、QTFPredは古典参照モデルに比べて、堅牢性･安定性を示したという評価を下している。
〖3〗安定性の確認　
　本論文では、｢様々なピークサイズにおいて、QTFPredが高い精度と安定したパフォーマンスを維持する｣ことを確認している(詳細は割愛)。この確認作業のため、 ランダム･ダウン･サンプリングにより、ピーク･サイズが様々なネストされた学習データセットが作成された。
❚考　察❚　
※　以下の計算及び数値は、本論文にあるわけではない、ことに注意。
㈠　MCF7(☞🐾17の参)に対するIOUスコア{0.77、0.66、0.58}と{0.87、0.86、0.75}を使って、|QTFPredの値ー FCNAの値|/ FCNAの値を試算すると、16.7%及び1.16%となる。数値は{QTFPred、FCNA、FCN}の順でであった。この結果は、限られたデータに対してQTFPredは、16.7%性能を上げた、という見方ができるだろう。この16.7%という数値は、かなり大きい(という印象)。
㈡　HeLa-S3(☞🐾20の壱)に対するピアソン相関係数⓵{0.70、0.61、0.36}、⓶{0.75、0.69、0.49}、⓷{0.78、0.74、0.60}を使って、|QTFPredの値ー FCNsignalの値|/ FCNsignalの値を試算すると、⓵14.8%、⓶8.70%、⓷5.41%となる。数値は{QTFPred、FCNsignal、BPNet}の順であり、⓵＝低ピーク群、⓶＝中ピーク群、⓷＝高ピーク群であった。こちらも、やはり限られたデータに対してQTFPredは、14.8%性能を上げた、という見方ができるだろう。この14.8%という数値も、かなり大きい(という印象)。
‖参　考‖　
㈠　学習時間　
　学習時間は、FCNsignalが一貫して最も速い(⓵2.58秒、⓶5.32秒、⓷14.1秒)。次いでBPNet(⓵6.61秒、⓶14.7秒、⓷40.5秒)。量子モデルは、遅い：QTFPred(⓵55.7秒、⓶119秒、⓷320秒)。ピーク群全体(⓵＋⓶＋⓷)で平均すると、FCNsignal(7.32秒)はBPNet(20.6秒)の2.82倍(本論文ママ)高速であったのに対し、QTFPred(165秒)は、BPNetの8.00倍(本論文ママ)、FCNsignalの22.5倍低速であった。量子(古典ハイブリッド)モデルなのに遅いのはなぜ？という疑問は、的外れであろう。古典モデルに量子回路というハードウェア･オーバーヘッドを追加しているのだから、遅いのは当然。
㈡　推論時間　
　 QTFPred(2.73秒)は、BPNet(0.529秒)に比べて5.16倍低速、FCNsignal(0.491秒)に比べて5.55(本論文ママ)倍低速であった。こちらも、遅いのは当然であろう。
㈢　 CPU メモリ使用量　
　BPNetと比較したQTFPredのCPUメモリ･オーバーヘッドが、すべてのピーク群で一定(0.31GB)であった。これは、量子回路シミュレーションが、データセットのサイズに関わらず固定コストを課すことを示唆している。

1⃣　概要　
　デンマーク工科大学他^🐾1の研究者は、以下タスクを、古典モデルと量子古典ハイブリッド･モデルで比較し、後者モデルが優れていると主張する論文(以下、本論文[*A-108])を発表した(25年8月29日)。タスク╏低分子医薬品の連続製造プロセスにおいて、原料に関する突発的な変動によって引き起こされる異常運転状態の検出。これは、｢正常な運転状態と異常な運転状態を識別すること｣とも言い換えられる。
🐾1　英ORCAコンピューター(量子H/Wスタートアップ、モダリティ:光)、デンマーク･ノボノルディスク(製薬企業)、米SiC Systems(エージェントAI開発スタートアップ)。
2⃣　量子古典ハイブリッド･モデル　
㈠　異常運転状態検出モデルのアーキテクチャ概要　
　タスクは、正常な運転状態と異常な運転状態を識別することあった。異常な運転状態がレアであることを鑑み、本論文の学習モデルは、教師なし学習とする。具体的には、敵対的生成ネットワーク(GAN)とする。本研究の枠組みでは、生成器は、正常な運転状態に、(確率分布からの)サンプルをマッピングするように確率分布を学習する。識別器は正常運転データとそれ以外のデータを区別する”判定境界”を学習する^🐾2。
　本論文では、単独のGANではなく、GANのアンサンブルを採用する。これは本論文が、｢単独のGANでは、広範囲の潜在的な異常を検出するには、探索の幅＝不確実性が不十分｣と考えるからである。アンサンブルのいずれかの識別器がデータを異常とフラグ付けした場合、異常検出モジュール(識別器)は、その時系列データを｢異常｣としてラベル付けする。
🐾2　その意味において、本論文のフレームワークは、GANを用いた逆強化学習と見做すことが可能と思われる(☞5⃣考察㈣)。
㈡　アーキテクチャの補足　
　本論文のGANは正確には、ワッサースタインGANである。ワッサースタインGANは、学習安定性が高く、高品質な結果をもたらすことが知られている。いわゆるmode collapse(最頻値崩壊)^🐾3にも強いとされるが、本論文は不十分として、量子技術(量子古典ハイブリッド･モデル)の採用を検討するに至った。本論文における量子古典ハイブリッド･モデルとは、GAN生成器の入力確率分布が量子回路から生成される確率分布であること、古典モデルとは入力確率分布が正規分布であること、を指している。
　生成器と識別器はどちらも、2つの隠れ層とLeakyReLU活性化関数^🐾4を持つフィード･フォワード･ニューラルネットワークで構成される。
🐾3　ニュアンス的には、最頻値地獄と訳した方が、しっくりくる。
🐾4　入力値が0未満の場合には出力値が入力値をα倍した値、入力値が0以上の場合には出力値が入力値と同じ値となる活性化関数である。通常、αには0.01が使われるらしい。
㈢　学習データ　
　医薬品原料であるロバスタチン^🐾5の製造プロセスをシミュレートするためにKTB1(KT-Biologics I)モデル^🐾6を使用する。同モデルのモンテカルロ･シミュレーションを実施し、正常な運転状態及び異常な運転状態の両方を表す時系列データセットを生成した。異常は、ラクトース濃度の段階的変化を実装することで導入された。
🐾5　いわゆるスタチン系医薬品。故に、高脂血症薬。英アストラゼネカが、クレストールという名称で製造販売している。
🐾6　プラント全体にわたるバイオ製造プロセス･モデル。GitHubを通じて自由にアクセスできるオープンソースモデル。透明性、可用性、柔軟性に優れる、とされる。
3⃣　量子技術　
　量子古典ハイブリッド･モデルで使用される量子回路として、NISQ実機^🐾7と量子シミュレータ^🐾8の2種類が採用される。本論文の量子技術は、この量子回路のみ。　
🐾7　光方式の量子H/W。具体的には、英ORCA Computing PT-2システム。
🐾8　詳細は記述されていない。なお、ノイズレス･シミュレータであることは、推量される。
4⃣　比較結果　
㈠比較指標　
　ROC(Receiver Operating Characteristic curve)、AUC(Area Under the Curve)を採用する。　
㈡　定量的な結果詳細　
　定量的な結果が示されているAUCのみ以下に示す。アンサンブルのメンバー数が①30と②60の2ケースに対して実験が行われた(☞5⃣考察㈤)。{❶量子シミュレータを使った量子古典ハイブリッドモデルのAUC、❷NISQ実機を使った量子古典ハイブリッドモデルのAUC、❸古典モデルのAUC}を示すと、以下の通り：①{❶0.409±0.012、❷0.324±0.026、❸0.280±0.023}、②{❶0.429±0.009、❷0.412±0.019、❸0.350±0.019}。①、②ともに、❶＞❷である。
5⃣　考察　
㈠　驚くべきことに、AUCが0.5を下回っている。AUC=0.5はランダムに(でたらめに)二値分類した場合のAUCに相当するから、通常教科書的には、AUCの最小値は0.5と書いてある。それ以下は、モデルとしてあり得ない、という意思表示である。理論的な最小値は、もちろん0である。
　AUC＜0.5は、本論文の文脈における異常検出が極めて困難なタスクであるとしても、｢全く実用的ではない｣ということにならないだろうか。
㈡　⓵＝(❶ー❸)/❸、⓶＝(❷－❸)/❸を試算すると、 ①{⓵46.1%、⓶15.7%}、 ②{⓵22.6%、⓶17.7%}となる。かなり、大きな”改善率”となっている。表記は4⃣㈡に準ずる。
㈢　本論文は、｢(古典モデルにおいて)正規分布以外の確率分布を用いることで、性能向上をもたらす可能性を排除できない｣としながらも、｢様々な代替分布を調査することは非現実的であり、計算コストも高い｣。つまり、｢量子回路にの出力が従う確率分布を生成器の入力確率分布として採用する方が、より広範な古典的確率分布を調査するよりも、リソースをより効果的に活用できる可能性がある｣と主張している。量子の有用性も、ここまで、身の丈を縮めたか･･･と、ある意味愕然とする。
㈣　本論文のフレームワークは、敵対的生成ネットワークを使った逆強化学習と見做すこともできるだろう。熟練エージェントが、データを正常運転と識別する様を観察して、正常と異常の境界を学習する、という描像であろう。
㈤　アンサンブルのメンバー数を30から60に増加させることで、誤検知が増加するか？が検証されている。結論として、メンバー数が増えても、誤検知は増加しなかった。
㈥　異常検出までに要する時間の短さは、❷＞❶であろうが、性能の低下に見合うのだろうか？
㈦　[*A-109]は、GANは｢学習された識別器は、生成器によって実現された確率分布を目標分布に近づける役割を果たせない｣とし、Slicing Adversarial Network(SAN)なるものを提案している。SANの詳細には触れないが、留意すべきは、量子に頼らなくても古典の範囲で性能を上げる手段は豊富に存在するということである。[*A-109]は識別器がダメと主張しており、それを是とするならば、生成器の入力確率分布をいじっている本論文の戦略は、ズレている可能性もあるだろう。AUC<0.5を鑑みると、そう思えてくる。

【0】はじめに
　量子機械学習のレビュー論文[*A-42]は、量子強化学習を対象外としている。このため、量子強化学習のレビュー論文を追加した。ここでは、独フラウンホーファー集積回路研究所^🐾1の研究者によるレビュー論文[*A-45](以下、本論文)を取り上げた(24年3月8日)。
🐾1　フラウンホーファー集積回路研究所(IIS)は、現在フラウンホーファー研究機構の中で最大の研究所であり、マイクロエレクトロニクスおよびITシステムのソリューションとサービスにおいて世界の指導的な立場にある。「認知センサー技術」と「オーディオ・メディア技術」は、当研究所の戦略的指針となる2つのテーマである。例えば、人工知能の統合など、イノベーションを起こし続けることで、研究開発を推進し、経済と社会に直接貢献する。
　出所：https://www.iis.fraunhofer.de/ja.html

【1】本論文のまとめ　
　本論文では、以下に示す4つのカテゴリー(1)～(4)に分けて、量子強化学習を評価している。
(1)　量子インスパイアード強化学習　
　以下のように要約されている。
㊀　探索と活用のバランスを改善することで、学習が高速化される。
㊁　古典的なQ学習等と比較して、古典コンピューターでは GPU パワーが少なくて済む。
㊂　学習率の変化に対してより堅牢である。

(2)　変分量子回路による量子強化学習　
　暗号学に触発された人工データセットを除いて、このアプローチには、量子優位性が保証されていない。

(3)　量子サブルーチンを使った量子強化学習
1⃣　射影^🐾2シミュレーション　
　射影シミュレーションは、ランダムウォークに基づいてシミュレーションを行う。”量子”射影シミュレーションは、ランダムウォークを量子ウォークに置き換えることで、量子化する。このため、量子射影シミュレーションは、2次加速を実現するとされている。
🐾2　ここで使用されている｢射影｣という文言は、量子力学において用いられる射影(例えば、射影測定や射影演算子等)とは関係がない。エージェントが他の考えられる状況に関連付けることで、未知の経験に対処できるという意味で、｢射影｣という文言が使われているらしい。
2⃣　量子方策反復法及び量子価値反復法　
㈠　生成モデル　
　ここで言う生成モデルとは、状態と行動のペア(s、a)でクエリされ、サンプル s′ ～ P(·|s、a)を生成するモデルを表している。サンプリングによってマルコフ決定過程の遷移行列が推定できるので、価値反復法を使って、最適な方策の近似値を取得できるという仕組みである。
　生成モデルでは、サンプル複雑性の2次加速が実現する。この2次加速は、グローバーのアルゴリズムに由来する。ここでのサンプル複雑性は、シンプルに、クエリ回数として定義されている。
㈡　エピソディック学習^❚補足❚　
　 エピソディック学習では、エピソードという試行期間が明確に存在するので、エピソード終了時点での”中間査定”が必要となる。この中間査定の結果として、エピソディック学習には｢後悔(regret)｣という概念が存在する。後悔とは、Kエピソード後の最適値関数とその近似関数との累積差として定義される。
　エピソディック学習を量子化することで、後悔を任意の精度に収めるためのサンプリング数において、指数加速が実現する(らしい)。
㈢　量子方策反復法
　量子コンピューターでQ値を評価し、その後、方策を古典デバイスで改善するというアプローチでは、量子加速は高々、多項式的とされている。
3⃣　量子ボルツマンマシン
　サンプリングにおいて2次加速が期待されるが、現在のハードウェアで実現できる可能性は低い。
❚補足❚　エピソディック学習[*A-46]
　エピソディック(強化)学習は、継続的強化学習と対比される。エピソディック学習は次のような学習プロセスを辿る：状態s_iのエージェントは、行動a_iをとり、遷移核p_i(・|s_i, a_i)に従ってサンプリングされた次の状態s_i+1を観測し、報酬r_i(s_i, a_i)を受け取る。
　概念的にはエピソードが無限長である継続的RLでは、定常状態の概念が重要となる。具体的には、継続的 RL アルゴリズムの多くは、学習データが、behavior policy(学習中の方策)の定常分布に従うことを必要とする。一方、エピソディック強化学習では、エピソードは有限長である。有限長エピソードのため、エピソディック学習では定常状態は存在しないと広く考えられていた。
　その違いにも関わらず、エピソディック学習におけるデータ収集方法は継続的RLと同じであり、その妥当性が疑われていたが、同じ枠組みで構わないことが証明されたらしい[*A-46]。有限エピソードの無限ループを使うことで、behavior policyが定常分布に従うような学習プロセスを構築できる(らしい)。

(4)　完全な量子強化学習
　エージェントと環境の両方を量子系とする、完全な量子強化学習でも、2次加速しか発見されていない。また、量子勾配推定法は、必ずしも量子加速につながらない、ことが示されている。

【2】アプリケーションに焦点を当てた結果　
　以下の各タスクにおいて、古典対応物に対して報告されている ”量子優位性”を列挙した(ただし、曖昧に表現されているものは、除外している)。
(1)　ロボット工学およびその他の制御タスクのための QRL　
㊀　パラメータ数の削減　→ただし、成功率の低下を伴う可能性あり(であれば、無意味)
㊁　学習安定性の向上
(2)　計画タスクの QRL
㊀　推論中における『潜在的な』高速化。
㊁　パラメータ数の削減　→ただし、収束は”遅い”。
(3)　複数エンティティのコラボレーション･シナリオにおける QRL
㊀　高速な収束
㊁　パラメータ数の削減

❚はじめに❚
　スイスの量子技術スタートアップTerra Quantum他^🐾は、｢テンソルネットワーク(TN)の多様なアプリケーションをレビューし、TNが量子コンピューティングにとって重要な手段であることを示す｣レビュー論文[*A-49]を発表した(25年3月11日@arXiv)。以下は、その｢まとめ｣である。
🐾 加シャーブルック大、米JPモルガン･チェース、米カリフォルニア工科大、米クオンティニュアム、米NVIDIA、米グーグル、米NASAエイムズ研究センター、米KBR、フィンランドのユヴァスキュラ大学、加ブリティッシュ･コロンビア大。
KBRは、｢世界中の政府や企業に科学、技術、エンジニアリングのソリューションを提供する｣。産業セクターは、Biotechnology & Drugsとなっている。
出典：https://jp.reuters.com/markets/companies/KBR.N

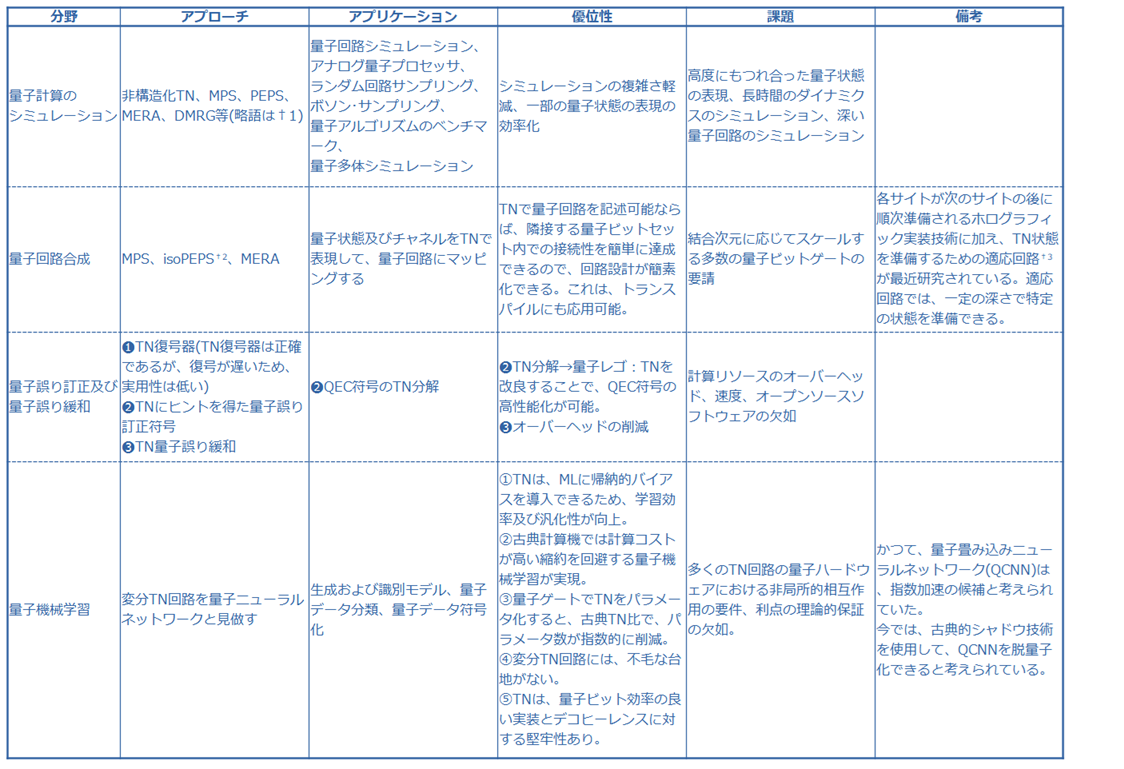
†1　MPS＝行列積状態、PEPS＝射影エンタングルドペア状態、MERA＝マルチスケール･エンタングルメント繰り込みアンザッツ、DRMG＝密度行列繰り込み群。MERAの訳語は、正式な訳語ではない(おそらく正式な訳語はない)。MERAは、isometry構造(下記†2参照)に、ユニタリTNが埋め込まれている[*A-50]。
†2　isometric PEPS。isometryとはスケール不変(等距離写像で写せる)という意味。同じ距離感を保っている構造が続いているテンソルネットワークという理解で良いだろう。MPSはisometryなTN。isometryなTNは、量子回路に自然にマッピングできる。PEPSは、isometryではないため、量子回路に(正確に)マッピングするには、指数関数的なボリュームの事後選択を要する。isometry条件を課したPEPSであるisoPEPSを使うと、(おそらく多項式オーバーヘッドで)量子回路にマッピングできる(はず)。
†3　適応回路は、回路の途中で測定を行い(いわゆる中間回路測定)、その後にそれらの測定によって決定されるゲート操作を実行できる量子回路。

【0】はじめに
　量子シミュレーションは、指数加速(⋍量子超越)が実現するキラー･アプリケーションと目されている。ユーザー目線での指数加速とは、全ての｢処理｣を含んだコミコミ時間での、指数関数的な時間短縮を意味する。古典計算の文脈であれば、｢全ての処理コミコミ｣は、ウォール･クロック時間という尺度で計測できるだろう。量子計算は、もう1～2捻りする必要があって、古典↦量子変換：入力状態の準備、量子↦古典変換：出力状態の読み出し、という事前処理及び事後処理が不可欠である。
　困ったことに、この事前処理と事後処理は、工夫せずに、素直に行うと、｢指数関数的に、時間を消費する｣。つまり、その場合は、純粋な計算処理プロセスにおいて指数関数的に時間を短縮^{❚補足1❚}したとしても、トータルでトントンになってしまう。従って、入出力に要する時間を｢指数関数的に遅くしない｣ことは、実のところ、非常に重要である。
　Quemix^🐾1と本田技術研究所(ホンダの研究開発部門)の研究者は、量子化学計算分野で共同研究を開始したこと及び、｢量子状態を読み出す新技術の共同開発に成功した｣と発表した(25年５月14日)[*A-52]。論文という形式では、arXivにて公開されている(25年5月13日付け。以下、本論文[*A-53]と呼ぶ)。本論文はザックリ言うと、情報抽出にかかる計算コストを、従来手法よりも低減できる｢読み出しプロトコル｣を開発した、という内容である。
🐾1　https://www.quemix.com/
❚補足1❚　正確にいうと、古典計算比で量子計算が削減できる対象は、計算ステップ数である。1計算ステップに要する計算時間を削減できるわけではない。トータル計算時間＝計算ステップ数×1計算ステップあたりの計算時間、である。古典計算を行うCPUあるいはCPU＋GPUという座組は、クロック周波数が高いので『1計算ステップあたりの古典計算は、量子計算よりも速い』。ただ、指数関数的に計算ステップ数を削減できれば、1計算ステップあたりの計算速度が、多少遅くても、トータル計算時間では速くなることが期待できる。別の見方をすると、2次加速であれば、この計算処理プロセスの段階で、古典計算機に負けることも十分有り得る。
　もちろん、この(上記の)議論と、入出力を含めたコミコミ(＝エンド･ツー･エンド)での議論は、異なる議論である。

【1】本論文の主張
　本論文は、以下を主張していると思われる：
(1)　量子状態を直接読み出すプロトコル(量子状態トモグラフィー)よりも、計算コストが低い、読み出しプロトコル(以下、本プロトコル)を開発した。
(2)　本プロトコルは、量子ビット数が多い量子回路において、優位性が実現する。
(3)　本プロトコルは、｢量子状態を完全に取得する必要がある｣場合においても有効である。
(4)　本プロトコルは、｢量子状態が関数展開の線形結合として、本質的に連続関数を表すと予想されるシナリオ｣において、特に有望である。

【2】事前整理
(1)　量子状態を読み出すプロトコル　
1⃣　量子状態トモグラフィー　
　量子状態トモグラフィーは、測定データから、未知の量子状態(における密度演算子)を推定する手法である。ただし、量子状態トモグラフィーの不忠実度(＝1－忠実度)は、量子ビット数とともに指数関数的に増加する。このため、量子状態トモグラフィーによって量子状態を読み出す場合には、量子ビット数に関して指数関数的な測定数(計算コスト)が必要となる。しかし、全てのアプリケーションにおいて、量子状態を完全に取得することが必要となるわけではない。量子化学計算においても基底状態エネルギーに焦点を当てる場合等では、量子状態の完全な取得は必要ない^{❚補足2❚}。
❚補足2❚　本論文には、量子状態を完全に再構成することが不可欠なアプリケーション･カテゴリーとして、2つのカテゴリーが上げられている。一つは、㊀｢流体シミュレーション、ポアソン方程式の解法などの計算物理学のアプリケーション｣である。もう一つは、㊁｢完全に読み出された完全な量子状態が、次の反復ステップの入力として使用される、自己無撞着場(SCF)に基づく非線形微分方程式を解く必要があるアプリケーション｣である。
　㊀は、CAE分野の量子シミュレーションと言える。㊁は、電子状態を求める必要がある量子化学計算である、と言える。
2⃣　 古典的シャドウ　
　コストを抑制した量子状態読み出しプロトコルとして、｢古典的シャドウ｣が注目されている。古典的シャドウは、測定データから、未知の量子状態を｢サンプリング･ベースで推定する手法｣である。具体的には、異なる基底で量子状態をランダムに測定し、古典的な事後処理を使用することにより、複数の期待値を同時に推定する。このため、必要な測定数を軽減できる。本論文では、｢古典的シャドウは、限られた測定データからさまざまな量子系の情報を抽出できる高い効率性と柔軟性を備えているため、急速に注目を集めている｣と記述されている。古典的シャドウは、｢量子状態の完全な取得は必要ない｣場面で活躍する、読み出しプロトコルである^{❚補足3❚}。
　古典的シャドウの実適用例として、マイクロソフト(Azure Quantum)による”化学系のエンドツーエンド量子シミュレーション”があげられる。この例は、相関電子系(である化学反応)のシミュレーションを、量子位相推定法(QPE)ではなく、変分量子固有値ソルバー (VQE)で実行した。詳しく言えば、｢DFT╏古典コンピューター｣＋｢VQE╏NISQマシン｣＋｢古典的シャドウ╏古典コンピューター｣という枠組みで実行した(こちらを参照)。
❚補足3❚
　古典的シャドウは、スコット･アーロンソンが考案した。アーロンソンは、｢量子系の完全な古典的記述を要求することは過剰であり、特定の性質(ターゲット関数)を正確に予測できれば十分な｣ことを指摘し、古典的シャドウを提案したのであった。
3⃣　本プロトコル　
　本プロトコルでは、不忠実度は、｢内積計算の回数｣に依存することが数値シミュレーションの結果から示された(以下の結果も、同じ)。そして、この｢内積計算の回数｣は、量子ビット数に依存しない^🐾2。そのため、本論文では、｢量子ビット数が増加するにつれて、本プロトコルが”量子状態トモグラフィー”よりも、優れた性能を発揮する可能性がある｣と主張している(と思われる)。古典的シャドウとの比較はなされていない(と思われる)。
　本プロトコルは、状態ベクトルを読み出すので、密度演算子を生成できる。つまり、量子状態を完全に読み出せるプロトコルだと考えられる。
🐾2　展開関数として正規化された離散化ローレンツ関数(☞(3)を参照)を採用した本論文の場合には、以下のことが、数値シミュレーションの結果から示された：内積計算の回数は、正規化された離散化ローレンツ関数の｢初期ピーク位置と最適ピーク位置間のハミング距離｣に、ほぼ比例する。

(2)　SWITCHテストとSWAPテスト　
　分かり難い表現であるが、どちらも、(量子状態を表現する方法の一つである)状態ベクトル(複素ヒルベルト空間のベクトル)の内積を計算する量子回路である。SWAPテストはSWITCHテストに比べて、量子回路がシンプルである。これは、SWITCHテストには、制御ゲートが必要なためである。位相因子を含む量子状態を読み出す場合には、SWITCHテストを要する。位相情報が不要な場合は、SWAPテストで十分である。

(3)　ローレンツ関数及び正規化された離散化ローレンツ関数　
　主に分光分析の分野で、スペクトルの波形を表現したり、バックグラウンドの前処理やスペクトル強度のフィッティングに使用される関数(らしい)。ローレンツ関数は、ガウス関数に比べて、ピークの裾が広がり、より実スペクトルに近い形状を表現できることが特徴である(らしい)。
　本論文では、正規化された離散化ローレンツ関数(以下、LF)が、展開関数として用いられている。LFは、正規化された離散化スレーター(型)関数をフーリエ変換することで、算出されている。LFには、3つの引数(a、d、k)がある。

【3】本プロトコルの説明　
1⃣　概要
　本プロトコルの仕組みは、以下の通りである：読み出したい量子状態(以下、ターゲット状態)と、｢適当な関数の線形結合を実装したパラメータ付き量子回路が生成する量子状態(以下、LCLF状態)｣とが一致するように、パラメータを古典的に最適化する。最適化されたパラメータを使って改めて、パラメータ付き量子回路によって生成させた量子状態を測定して得られた結果が、ターゲット状態の測定結果である。
　関数は適当で良いが、本論文では、X線スペクトル解析を事例として取り上げているので、LFが選択されている(と理解している)。
2⃣　補足　
　ターゲット状態と LCLF状態の一致度(忠実度)は、２つの状態の内積を計算することで評価する。この計算は、量子回路で行う。具体的には、SWAPテストもしくはSWITCHテストを用いて、計算する。
　パラメータの最適化計算は、古典的に行う。具体的には、メトロポリス法を適用して、不忠実度(＝1－忠実度)が最小となるように最適化を行う。パラメータは、関数の線形結合における結合係数である。なお、LF同士の、重なり行列の計算も古典的に行われる。
3⃣　計算コスト　
　本プロトコルの古典計算にかかる計算コストは、次のように計算される：まず、重なり行列を計算するには、O(n²×M)の計算コストが必要である。ここで、nは、線形結合(における足し上げ)に用いられるLFの個数である。Mは、重なり行列を計算するために用いられる数値積分の計算コストである。(X線スペクトル解析のための)固有値方程式を解くには、O(n³)の計算コストが必要である。まとめると、古典計算のトータル計算コストはO(n_iter･max(n²×M,n³))となる。ここで、n_iterは古典計算における反復回数である。
　本プロトコルの量子計算にかかる計算コストは、O(c×m_iter/ε²)である。ここで、cは、ターゲット状態を準備するためのコストである。m_iterは、最適化に用いる内積計算の実行回数である。εは計算精度である。
　m_iter ≦ n_iterが満たされる(らしい)。SWAPテストとSWITCHテストに必要な計算コストは、cよりも小さいと仮定され(無視され)ている。またc自体、最悪の場合は指数関数的なコストとなり得るが、とりあえず、効率的に準備が可能であるケース^🐾3を想定して、深入りを避けている。
🐾3　特定のケースでは、多項式コスト若しくは線形コストで、状態準備可能である。本論文では、｢平均場近似が有効なケース｣等が上げられている。

【4】シミュレーション結果
(1)　本プロトコルでは不忠実度が、量子ビット数に依存しないことを示したシミュレーション
　適当なターゲット状態^🐾4と、適当なLFを与えて、掲題のシミュレーションを行った。適当なLFとは、適当な引数^🐾5を与えたことを意味している。また線形結合に使ったLFの個数は3である。
🐾4　|ψ(x)⟩ ∝ exp(−(32(x −0.5)/3)²)+ 0.4 exp(−(16(x −0.25))²))　(本論文ママ：最後の”)”は誤植と思われる。また、∝を＝とするには、1/2を掛ければ良い。)
🐾5　3個のLFの引数a、k、ｄはそれぞれ以下の通り：a = (0.360, 0, 1.672, 0.490)、k/N = (0.25, 0.4375, 0.5)、d = (0.380, −0.517, 1.272)。ただしN＝2ⁿ、nは量子ビット数。

(2)　SWAPテストを使用した場合でも本プロトコルが機能していることを示したシミュレーション　
　量子状態の確率分布を推定した。古典計算の反復回数を増やすと、残差が0に近づくことが示された。

【5】感想
　Quemixとホンダが実行したXAFS(X線吸収微細構造)計算全体を、マイクロソフトの結果(☞【2】(1)2⃣参照)：｢DFT╏古典コンピューター｣＋｢VQE╏量子コンピューター｣＋｢古典的シャドウ╏古典コンピューター｣と対比させると、｢DFT╏古典コンピューター｣＋｢PITE╏NISQマシン｣＋｢本プロトコル╏古典コンピューター＋量子コンピューター｣となる。PITE＝確率的虚時間発展法であり、Quemixのオリジナル。
　局地戦となるが、本プロトコルと古典的シャドウとの比較結果は、どうなるのだろうか。

【0】はじめに　
　時間領域天文学^🐾1に新たな時代が到来するらしい。様々なタイプの望遠鏡^🐾2を使って、多様かつ大量の観測データが収集され、利用可能となる時代には、変動天体^🐾3を自動的に特定する手法の開発が最も重要な研究課題の一つとなる(らしい)。そこで、機械学習の出番という次第である。機械学習は、時間領域天文学においても様々な役に立つが、新たな種類の突発天体(あるいは突発現象)^🐾4を｢外れ値として識別する｣＝｢検出する｣上で重要な役割を果たす(らしい)。
　立教大学･大阪大学･理化学研究所･東北大学の研究者は、突発天体検出タスクにおける量子機械学習の可能性を検討･検証した論文(以下、本論文[*A-55])を発表した(2025年7月2日@The Astrophysical Journal^🐾5)。ザックリ言えば、検出性能において、量子機械学習＞古典機械学習、という内容。
🐾1　変動天体(☞🐾3)の研究を行う天文学。
🐾2　様々なタイプとは、｢光学望遠鏡のみならず、重力波望遠鏡なども含む｣という意味。日本であれば、神岡鉱山の地下約200メートルのトンネル内に設置されていKAGRA(神楽)という重力波望遠鏡がある。
🐾3　変動天体とは、光度や位置などが時間とともに変化する天体を指す。
🐾4　突発天体は英語だと、transient source。突発現象だとtransient event。意味は同じ(同義異音)。電磁波の強度が急激に増大する天体を指す(→https://astro-dic.jp/transient-source/)。恒星フレア、連星系の爆発、高速青色光トランジェント、ガンマ線バースト、活動銀河核などが、突発天体としてあげられる。
🐾5　天文学と天体物理学を専門に扱う学術雑誌で、出版は英国物理学会出版局。2015年からオンライン専用になった(らしい)。

【1】目標　
　4XMM-DR14^🐾6カタログに含まれるX線光度曲線^🐾7で学習させた量子機械学習モデルを用いて、突発天体のX線光度曲線における異常事象を同定し、突発天体事象を検出する。
🐾6　XMM-Newton Serendipitous Source Catalog, Fourth Data Release。XMM-Newtonは、欧州宇宙機関(ESA)のX線天文衛星。軟X線帯域(0.2～12 keV)において広い有効面積と30フィート径の広い視野を有する3つの検出器を備えている。X線データを効率的に蓄積しており、4XMMカタログは世界最大級のX線帯域データベースの一つとなっている(らしい)。
🐾7　光度が変化する天体の光度を、時間の関数として表した曲線。英語では、ライトカーブ(light curve)。一般に、縦軸に天体の明るさ(等級)を取り、横軸に時刻をとる。周期的な変化を示すものは、時間の代わりに位相を採用する。天体の種類によって光度曲線にはさまざまな特徴が見られる(→https://astro-dic.jp/light-curve-3/)。

【2】主張
　本論文は、以下を主張する：
(1)　量子機械学習モデルは、真陽性率^🐾8において、古典機械学習モデルをわずかに上回る。
🐾8　一般的な分類タスクの文脈では、再現率(recall)と呼ばれる。感度(sensitivity)とも呼ばれる。真陽性率という文言は、医療系の文脈で多く用いられる(曰く、疾患ありのヒトが、陽性と診断される割合)。
(2)　量子機械学習モデルと古典機械学習モデルとの間で、偽陽性率^🐾9に明確な差は見られない。
🐾9　一般的に知名度が高い特異度を使って表すと、偽陽性率＝1ー特異度(specificity)。先の例で言えば、偽陽性率は、｢疾患なしのヒトが、陽性と誤診される割合｣。
(3)　量子機械学習モデルは、汎化性能が高い。

【3】本研究の学習モデル　
(0)　古典機械学習モデル：CLSTM　
　学習モデルは、時系列データ処理にあたっての定番モデルであるLSTM(Long Short Term Memory)を採用している。量子版のLSTMをQLSTMと表記するので、量子版ではないーつまり古典版の(通常の)LSTMを以後、CLSTMと表記する。CLSTMは忘却ゲート、入力ゲート、出力ゲートという3つのゲートによって学習を行う。忘却ゲートは、入力データに基づいて、セル状態(長期記憶)から情報を削減する。入力ゲートは新たに、長期記憶に保存するべき情報を決定する。出力ゲートは、文字通り情報を出力する。なお、本論文では、PyTorchのLSTM クラスを使用してLSTMを実装している。

(1)　量子機械学習モデル：QLSTM　
　CLSTMの量子版QLSTMは、CLSTMの3つの各ゲートにおいて使用される全結合層を、量子回路(パラメータ付き量子回路、つまりアンザッツ)に置き換えることで構築する。なお、QLSTMは量子シミュレータ上に構築されたのであって、物理的なデバイスを用いて構築されたわけではない。
　古典データの量子符号化には、ZZ特徴量マップを使用する^🐾10。ZZ特徴量マップは、まず、アダマール･ゲートを使用して重ね合わせ状態を作成する。次に、入力値に基づいて状態ベクトルをZ軸周りで回転させながら、CNOTゲートを介して量子ビット間のエンタングルメントを生成する。ZZ特徴量マップは、非常にポピュラーな特徴量マップである。量子特性を利用して、古典的には再現が困難なマッピングを実現する能力で知られている。
　アンザッツは、C20と呼ばれるアンザッツを使用する^🐾11。この量子回路は、｢CNOT ゲートを使用して各量子ビットを隣接する量子ビットとエンタングルさせ、すべての量子ビットを X、Y、Z軸を中心に回転させる｣。
🐾10　正確には、3種類の特徴量マップを比較検討しているが、煩雑さをさけるため、最終的に選択されたZZ特徴量マップのみを取り上げた。
🐾11　正確には、3種類のアンザッツを比較検討しているが、煩雑さをさけるため、最終的に選択されたC20のみを取り上げた。

【4】学習データ　
(1)　概要　
　XMM-Newtonカタログにおいて、活動銀河核(AGN)^🐾12が重要な分布である。故に、正常学習データセットは、AGN類似光度曲線をシミュレートすることによって生成する。異常学習データセットは、AGN類似光度曲線に、準周期的噴出(Quasi-Periodic Eruption：QPE)^🐾13のようなフレアを追加することで作成する。
　現在の X 線観測において確認された QPE イベントが乏しいことを鑑みると、上記のようにデータセットを構築することは重要である。なお、単一の天体に対して複数の観測データが利用可能な場合は、露出時間が最も長いデータのみを解析する。
🐾12　強い電磁波を放射している銀河中心部領域を言う。出所：https://astro-dic.jp/active-galactic-nucleus/
🐾13　系外銀河の中心付近で X 線の光度曲線が準周期的にバーストを起こす現象。出所：https://www2.ccs.tsukuba.ac.jp/Astro/colloquia/ja/2025/03/26/suzuguchi/

(2)　データセットの作成　
1⃣　正常データセット
　正常データセットに関しては、AGNに適切なパワー スペクトル密度(PSD)を仮定し、逆フーリエ変換を実行する。PSD の形状は、べき乗関数として設定される。具体的には、以下のように作成された：
㊀　PSDの傾きは正規分布からランダムに決定され、暫定的な正規化値を用いて逆フーリエ変換により光度曲線が生成される。露光時間とビンサイズはそれぞれ100ksと1ksに設定される。
㊁　次に、一様分布からサンプリングされた過剰分散に基づいて、適切なPSD正規化が光度曲線に組み込まれる。
㊂　光度曲線を標準化する。
2⃣　異常データセット　
　異常光度曲線は、1⃣の方法でAGN類似光度曲線をシミュレートし、次にQPE類似フレアを重ね合わせることで生成される。QPEフレアは、デューティ･サイクル、振幅、持続時間で特徴付けられる。
　デューティ･サイクルは割愛。振幅は、フレアの検出可能性に大きく影響するため、1.1、1.5、2.0、3.0 の固定振幅を持つ 4つの異常データセットを作成する。振幅1.1は、観測された QPE 振幅の最小値にほぼ​​相当する。持続時間(パラメータ)は、過去の研究によって提供された分布から、ランダムにサンプリングされる。

(3)　3つのデータセット　
　正常データセットと異常データセットからなる時系列データセットが3セット用意されている。それらは、セットA、B、Cと呼称される。
1⃣　セットA
　データセットの種類ごとに100本の光度曲線が生成される。セットAの正常データセットは、LSTMモデルの学習に使用される。
2⃣　セットB　
　正常光度曲線1000本と異常光度曲線1000本で構成される。このセットは、学習済みLSTMモデルの性能を評価するために設計されている。
3⃣　セットC　
　データセットの種類ごとに9つの光度曲線を含むより小規模なセットであり、光度曲線の再現におけるLSTMモデルの精度を視覚化するために使用される。

【5】学習　
(1)　量子と古典に共通した学習　
　セットA(正常光度曲線100本と異常光度曲線100本)を用いて、CLSTMモデルとQLSTMモデルの両方を学習する。正常データセットの70%が学習に使用され、残り30%は、各学習エポック後の性能評価に使用される。
　次に、学習可能なパラメータを最適化し、予測値と実測値の平均二乗誤差(MSE)を低減する。最適化にはAdaGradを採用した^🐾14。初期学習率は0.05に設定され、3エポック連続して、MSEの減少が0.001未満の場合、学習率は半分に減らされる。学習エポックの総数は50に設定された。｜為参考・・・CLSTM、QLSTM共に、隠れ層の数は4で、学習可能なパラメータの数は133個である。
🐾14　AdaGradを選択した理由は、以下の通り：Adamなどを検討した結果、AdaGradは損失を迅速に削減するための最良の選択肢の1つであることがわかった。

(2)　量子に固有の学習　
　QLSTMモデルでは、ノイズがなしとノイズありの2つの条件で、量子回路をシミュレートする。ノイズなしシミュレーションには、加Xanadu^🐾15のPennylane^🐾16が提供するlightning.qubitシミュレータ^🐾17を使用する。ノイズありシミュレーションには、米IBMが提供するシミュレータAerSimulator^🐾18を使用する。ノイズモデルは、ibm_brisbane^🐾19に基づいて作成された。
　ノイズを含む学習のシミュレーションは時間がかかるため、学習エポック数を3に制限している。ただし、パラメータは、ノイズのない学習から決定された値で初期化し、QLSTMモデルが数ステップで低い損失値を達成できるようにしている。
🐾15　光方式の量子コンピューターを開発しているカナダのスタートアップ。正確に言うと、モダリティはスクイーズド光(連続変数量子ビット→連続変数なので正確には、qubitではなくqumode)で、測定型量子コンピューターを開発している。連続変数量子ビットは(対応するヒルベルト空間の次元は無限次元なので)、量子機械学習に有利とされ、Xanaduは量子機械学習を最重要分野としている(URLは、https://xanadu.ai/)。量子誤り訂正符号には、GKP符号を用いる。
🐾16　量子機械学習用Pythonライブラリー。18年4月にリリースされた。
🐾17　Lightningは、｢量子機械学習アプリケーションに高いパフォーマンスを提供する｣ように設計された量子シミュレータ。C++で記述され、Pythonからアクセス可能なLightningファミリーには、lightning.qubitとlightning.gpuの2つのシミュレータがある。lightning.gpuは、lightning.qubitのGPUエクステンションである。LightningはPennyLaneとシームレスに統合されている。
出典：https://www.xanadu.ai/products/lightning/、及びhttps://pennylane.ai/devices/lightning-gpu
🐾18　Aerは、Qiskitのシミュレータ･モジュール。言わずもがなであるが、QiskitはIBMの量子プログラミング用SDK。Aerには、AerSimulator、AerStatevector、AerDensityMatrixがあるらしい。
　PennyLane-Qiskitプラグインが提供するqiskit.aerデバイスを使用すると、PennyLaneを使用して、Qiskit Aerが提供するバックエンドとシミュレータ上で量子機械学習モデルをデプロイして実行することができる。出典：https://docs.pennylane.ai/projects/qiskit/en/stable/devices/aer.html
🐾19　127量子ビットの超伝導方式量子コンピューター。

【6】結果　
(1)　真陽性率と偽陽性率を使った評価　
　データセットBを使用する。本論文は、以下のように主張している：QLSTMモデルは、真陽性率においてCLSTMモデルをわずかに上回る(→ほぼ同じに見える)。偽陽性率については、明確な差異は見られない(→これは、主張通りであろうか･･･)。
　真陽性率と偽陽性率のシミュレーション結果から、およそ10⁻³という低い偽陽性率と、およそ0.8という比較的高い真陽性率を達成できる｢しきい値｣として3.0を選択している。この｢しきい値｣は、XMM-Newtonカタログから、突発天体を検出(識別)するために使用される。

(2)　汎化性能　
　QLSTMは、突発天体候補を113本検出した。CLSTMモデルは85体であったため、単純計算で約1.3倍となる。本論文は、この結果は｢QLSTMの真陽性率がCLSTMモデルよりも高いことと整合している｣としている。
　ただ、これはあくまで候補であって、本当に｢検出した｣ということにはならない(はず)。ゆえに、約1.3倍というのは、過大評価かもしれない。

【7】感想等　
(1)　一言で言い表すと『量子特徴量を使うと、結果が良かった』であろう。しかし、｢わずかに真陽性率が高い｣と｢検出数3割り増し｣との間には、ギャップを感じる。
(2)　本研究は、検出性能に関して量子と古典を比べている。量子加速については、次のように述べられており、射程外である：
　古典コンピュータと量子コンピュータを頻繁に切り替えるLSTMのようなモデルは、実際の量子コンピュータへのアクセスにかなりの待ち時間をもたらす。そのため、全体のプロセスに非常に時間がかかり、実際の量子計算には実用的ではない。計算が完了したとしても、そのメリットは限られている可能性がある。したがって、量子モデルの文脈では、根本的に異なるアーキテクチャを探求する方が有利かもしれない。

【0】はじめに　
　註）本稿での量子有用性とは、IBMが使っている意味(https://www.ibm.com/jp-ja/think/insights/what-is-quantum-utlity)ではなく、量子的な手法を使うことで古典的な手法を使うよりも、｢何らかの良い結果｣が生じるくらいの漠然とした意味で使っている。
(0)　放談(つまり、読まなくて良い)　
　鉄腕アトム(1951年～)、ドラえもん(1969年～)、マジンガーZ(1972年～)、ガンダム(1978年～)等々^🐾1を輩出した日本は、精神的にも物理的にも、確実にヒト型ロボット先進国であった^🐾2。2000年にホンダがアシモを発表したときは、世界中のロボット研究者が度肝を抜かれた(例：当時世界最先端と言われていた早稲田大学の研究者が、腰を抜かした、と新聞報道された)。勢いそのままにアシモは、同年の紅白歌合戦で、(物理的にも社会的にも完全に抹消された、かつての国民的アイドル･グループ)SMAPと共演している[*A-56]。
　その後、ロボティクス(ロボット工学)は、他の先端技術と同じように、何度か冬の時代を経験した。あのアシモも、2022年静かに引退した。グーグルもヒト型ロボット開発を止めてしまった^🐾3。しかし、世界(主に米国及び中国)では密かに、スタートアップがヒト型ロボットの開発を粛々と進めていた(☞【5】追記)。ロボティクスは、フィジカルAIの文脈で”再び注目”されるようになったと思われるし、そのきっかけはNVIDIAのジェンスン･ファンCEOの発言であろう。
🐾1　アトム･ドラえもんとマジンガー･ガンダムを同列に論じることには、かなり無理がある(が併記した)。エヴァンゲリオンは、ロボットなのか？は議論しない。
🐾2　産業用ロボットでも、ファナックと安川電機がビッグ4に含まれている。他はABB(スイス)とクーカ。クーカは元ドイツ企業で、2016年に中国･美的集団に買収された。美的集団は、東芝の白物家電事業も(同年に)買収している。
🐾3　例えば、2013年に(日本の宝が外国企業に買収されたと世間がザワついた)東大発スタートアップSCHAFTは2018年に解散させられた。24年にロボット開発部門は閉鎖され、研究者たちはPhysical Intelligenceを立ち上げた。その一方で、グーグル(ディープマインド)はロボティクス用基盤モデルGemini Roboticsを開発。Apptronik社と協業して、ヒト型ロボットの開発を進めている。

(1)　本題　
　ロボットは複数の関節の動きが相互に依存する複雑なシステムであり、幅広い計算課題を伴なう。関節数が増加すると、それらの計算課題を解くために必要な時間も大幅に増加する。計算時間の増大は、複数の関節構成でエンド･エフェクタ(ロボット･ハンド、ロボットの手)の位置が同一になる冗長マニピュレータ(ロボット･アーム、ロボットの腕)において特に顕著になる。このような場合、単一の解析解を求めることは一般的に不可能である。柔軟で応答性の高いロボット動作を実現するには、多くの可能性から、有効な関節角度の組み合わせの決定(逆運動学計算)を迅速に行うことが不可欠であり、そのためには高速計算が不可欠である。そこで、量子コンピューターの出番という次第である(⤵補足)。なお、本論文の議論は、特定のロボット(ヒト型ロボットあるいは産業用ロボット)に限定されるわけではない。
　芝浦工大他^🐾4の研究者は、｢量子回路が、順運動学及び逆運動学計算^🐾5を実行できること｣を実証した論文(以下、本論文[*A-57])を発表した(25年8月8日^🐾0@scientific reports)。本論文は、量子シミュレーターと実機の両方を使った実験結果から、｢量子もつれを考慮した量子計算｣は古典計算に比べて、｢制御精度が高く、収束が速い｣と主張している。しかし、この主張は、やや怪しいと思われる。なお、本論文は、誤植が多いと思われる。
　⤴補足・・・高速計算が不可欠だから量子コンピューターというのは、やや安直な発想と思われるかもしれない。しかし、本論文における重要な発想は、｢量子ビットは3次元球面上の点を自然に表現できるから、運動学計算との親和性が高い｣という発想である。
🐾4　早稲田大学、富士通。
🐾5　関節変位からマニュピレータの位置を計算することを、｢順運動学計算｣と呼ぶ。なお本論文では、回転関節のみを考えているため、関節変位＝関節角度である。目標エンド･エフェクタ位置を達成するために必要な関節角度を計算することを、｢逆運動学計算｣と呼ぶ。
🐾0　Same numbers。わかる人にはわかる。

【1】本論文の主張　
　本論文は、以下を主張する：
　｢量子もつれを発生させた量子回路を用いた逆運動学計算は、迅速に収束し正確である｣。
迅速に収束の意味は【3】(1)2⃣を参照。正確の意味は【3】(1)1⃣を参照。

【2】本論文のセットアップ　
(0)　計算環境等　
1⃣　量子シミュレーション
　やや面倒くさいことにシミュレーションは、㊀Jupyter Notebook^🐾6＋ローカルPC環境と、㊁量子シミュレーターの2パターンで実行されている。どちらも、ノイズは考慮されていない。㊀はWSL2^🐾7を介してLinuxベースで実行するWindows 11 PC上のJupyter Notebook環境内で、Qiskit^🐾8を用いて行われた。㊁は、富士通の40量子ビット量子シミュレーターmpiQulacs^🐾9が使われた。
🐾6　オープンソースソフトウェアのwebアプリケーション。
🐾7　WSL2(Windows Subsystem for Linux 2)は、WSLの第2版。WSLは、仮想化技術を用いて、Windows上でLinuxカーネルを実行する。
🐾8　最も有名で、最も使われている米IBM製の量子プログラミング用SDK。ただし、量子機械学習では、加XanaduのPennyLaneの方が、有名で使用頻度も高い？
🐾9　Qulacsをベースとした量子シミュレーターで、英ARMの48コアCPUであるA64FX CPUに対して最適化されているらしい。
2⃣　実機を使った実験　
　理研と富士通が共同開発した64量子ビット超伝導量子コンピュータが使用された。

(1)　逆運動学計算のアルゴリズム
　パラメータ付き量子回路のパラメータを、古典的な最適化計算で最適化することにより、 逆運動学計算を行う。最適化計算は、与えられる目標終点位置(x座標、y座標、z座標)と量子回路による計算結果との差を最小化するように行われる。本論文の場合、エンド･エフェクタの目標終点位置を達成するために必要な関節角度が、最適化計算で求めるべきパラメータである。言わずもがな、最適化計算は、反復計算である。
　最適化アルゴリズムには、COBYLA(Constrained Optimization BY Linear Approximation)が使われている。COBYLAを選択した理由は、Qiskitとシームレスに統合できるため、と説明されている。

(2)　量子技術の導入¦量子もつれという呪文の詠唱　
1⃣　入力状態準備　
　古典入力変数が関節角度であるから、古典量子変換は不要である。”角度を、角度符号化する”こと(つまり、そのまま)で量子入力状態を準備することができる。1量子ビット回転ゲートの量子操作で、ロボット関節の動作を表現することができる。
2⃣　量子もつれ、及びモヤモヤ　
　少なくとも、量子もつれが発生していない量子回路に、量子優位性は発現しないだろう。ということで、本論文では、｢ロボットの腕に、量子もつれを発生させている｣。こう書くと怪しく感じるが、とりあえず純粋に数学的に考えればモヤモヤは晴れないものの、怪しさは消える。
　最も標準的な量子もつれの生成は、量子ゲート操作で言うと、アダマールゲート＋CNOTゲートで行える。そして、2量子ビット回転ゲートの実装は、アダマールゲート＋CNOTゲート＋1量子ビット回転ゲートで行える^🐾10。つまり、2量子ビット回転ゲートを実装すると、もれなく、量子もつれが付随する。あとは、2量子ビット回転ゲートとロボットの腕を｢物理的な意味合い｣で結び付ければ、解決である。本論文では、2量子ビット回転ゲートの｢物理的な意味合い｣を、同じ1量子ビット回転ゲートを2つの量子ビットに同時に作用させること、としている。
　ここまで来ても、2量子ビット回転ゲートの｢物理的な意味合い｣がピンとこない。物理的な意味合いがピンとこなければ、数学的トリックに過ぎないので、｢ロボットの腕に、量子もつれを発生させる｣ことに対するモヤモヤは晴れないと思われる(☞【4】)。
🐾10　Qiskitでは、アダマール＋CNOT＋R_z。

【3】比較結果及び評価　
(0)　比較のセットアップ　
　複数の逆運動学計算解を持ち、最適化を必要とする多自由度ロボット･アームについて、量子もつれがある場合とない場合の両方で、量子回路の収束挙動を検証した。具体的には、リンク･ロボットモデルを使用した。リンク1の根元であるジョイント1は、X、Y、Z方向に3つの回転自由度を持ち、リンク2の根元であるジョイント2も同様に3つの回転自由度を持つ。
　量子計算の結果を、標準的な最適化手法^🐾11を用いて得られた結果と比較した。
🐾11　SciPyを使った最適化計算のようである。

(1)　シミュレーション結果　
0⃣　前説　
　❶標準的な最適化手法(SciPyを使った最適化計算)、❷ローカル環境^🐾12×量子もつれなし、❸ローカル環境×量子もつれあり、➍ノイズなし量子シミュレーター×量子もつれあり、について比較した。最適化計算における反復回数は、10回及び30回が採用されている。
🐾12　【2】(0)1⃣の㊀を参照。
1⃣　比較した結果と意見　
　ユークリッド誤差＝√(x座標の誤差)²＋(y座標の誤差)²＋(z座標の誤差)²で、比較する^🐾13。誤差＝与えられたエンド･エフェクタの座標値と、計算されたエンド･エフェクタの座標値との差、である。まず、本論文の数字をママつかうと、❶{1.49、1.13}、❷{1.96、1.85}、❸{0.99、1.08}、➍{0.85、1.21}である。なお{･、･}は、{反復回数10回の値、反復回数30回の値}である。
　この結果から、以下のことがわかる：❷の結果が悪すぎる。➍の反復回数10回がベスト。❶と❷は反復回数30回の方が誤差小であるが、❸と➍は反復回数10回の方が誤差小である。❷と❸の比較から、量子もつれの影響は大きい。❸と➍の比較から、シミュレーターの違いは無視できない。❷及び❸は反復回数の違いが小さいが、❶及び➍は大きい(特に➍は大きい)。
　まとめると、｢量子もつれは、誤差を縮小させる｣(計算が正確)ということになるだろう。なお普通の感覚だと、信頼性の問題から、➍より❸を採用したいところである(☞4⃣参照)。
🐾13　本論文も、基本的には、ユークリッド誤差で比較している。
2⃣　本論文の主張　
　既述通り、❸と➍では、反復回数10回の方が誤差小である。この事実に対して本論文は、｢古典最適化器における局所的最小値または過学習挙動の存在を反映している可能性がある｣との見解も併記しつつ、｢量子もつれが、最適化の初期段階に最も大きく寄与することを示唆している｣と楽観的な意見を述べている。
　本論文は、反復回数10回の方が誤差小であることをもって、迅速に収束すると主張しているが、これは、かなりアグレッシブではないだろうか。
3⃣　根本的な疑問　
　最適化計算自体を複数回実施していないのか？は、根本的な疑問として浮かぶ。念の為、複数回実施について具体的に述べると、本論文で目標として与えられたエンド･エフェクタの座標値は(0.6,1.0,0.2)のみである。これを複数の座標値で与えて、本論文で行った計算と同じ計算を行えば良いと思われる。複数回実施しなければ、確定的なことは言えないように思われる。
4⃣　為参考：誤植の疑い　
　表3の｢Local: eith entanglement｣のような単なる表記ミスとは異なる誤植に関して、いくつか存在すると思われる。
㈠　まず、本論文に、｢30回の反復後、X-Y-Z座標におけるユークリッド誤差は、ローカル環境×量子もつれなし(本稿では❷)で約1.85 m、ローカル環境×量子もつれあり(本稿では❸)で約1.18 mとなり、全体的な位置誤差が36%減少した｣という記述がある。素直に計算すると、❷→√(0.93)²＋(1.57)²＋(0.32)²＝1.85(1.85262)となり、問題ない。しかし❸→√(0.62)²＋(0.82)²＋(0.33)²＝1.08(1.07968)となって合わない。誤差も36%ではなく、42%減少する。
㈡　先の誤植疑いに重大性はないが、次の誤植疑いは、やや重大性がある。本論文は、｢(量子もつれありの)量子シミュレーターは、わずか10回の反復(誤差1.17 m)で、30回の反復(1.21 m)と、ほぼ同じ精度を達成した｣と記述している。30回の場合、√(0.56)²＋(1.06)²＋(0.16)²＝1.21(1.20946)となり、問題ない。しかし、10回の場合は、√(0.62)²＋(0.58)²＋(0.00)²＝0.85(0.84900)となり、合わない。もし1.17mが正しければ、➍の反復回数10回はベストにならない。❸{0.99、1.08}、➍{0.85、1.21}→{1.17、1.21}となるからである。これだと文句なしに、➍より❸が良い。そして、❸{0.99、1.08}、➍{1.17、1.21}の方が、ビジュ的に肚落ちする。➍の10回反復と30回反復の差も、いい感じになる。なお、➍におけるz座標の誤差が0.0から0.8になると、0.85が1.17になる。
㈢　本論文では、比較指標がsquared errorとなっている。単位がm²であることもあり、squared error＝(目標値ー計算値)²であると思われる。しかし、squared errorなのに負値が存在している(❶の反復回数10回、x座標)。
㈣　本論文中では、squared errorのユークリッド誤差が計算されていると思われるが、その場合、単位はm²になると思われる。しかし、本論文中の表記は、mである。

(2)　実機による実験結果　
0⃣　前説　
　本論文では、実機による結果は、ノイズ(の影響)のため信頼性が低い結果しか与えないと見做されてるのかもしれない。❺量子もつれなし、❻量子もつれあり、で比較している。
1⃣　比較した結果と意見　
　❺{1.87、1.83}、❻{0.59、0.94}である。この結果から、以下のことが分かる：量子もつれは誤差を(劇的に)縮小させる。量子もつれがある場合、反復回数10回の方が誤差が小さい。この傾向はシミュレーションの場合(❸及び➍)と同じであるが、違いが大きすぎるように思われる。❻の反復回数10回の誤差が小さすぎる(❶～❻でベスト)。
　ノイズなし量子シミュレーターの結果➍{0.85、1.21}→{1.17、1.21}よりも、ノイズあり実機の結果❻{0.59、0.94}の方が誤差が小さいというのも、やや理解に苦しむ。
2⃣　複数回の実施　
　シミュレーションの場合と同じである。
3⃣　為参考：誤植の疑い　
　本論文に｢30回の反復後、誤差は、(量子もつれなしの場合の)約1.84 mから、(量子もつれありの場合の)1.04 mに減少する｣という記述がある。量子もつれなしの場合、√(0.59)²＋(1.70)²＋(0.35)²＝1.83(1.83319)であり、ほぼ問題はない。一方、量子もつれありの場合、√(0.69)²＋(0.60)²＋(0.20)²＝0.93(0.93600)となって、合わない。

【4】考察　
　本論文は、量子もつれの利用について、次のように総括している：｢提案手法は量子もつれを利用しているものの、親(関節)から子(関節)への一方向の依存関係しか捉えておらず、量子もつれが持つ双方向の相互作用を十分に活用していない。これは、量子コンピューティング手法で検討されてきた量子もつれを伴う量子計算技術を十分に活用していないことを意味する｣。
　つまり、｢量子もつれを利用して、性能を上げたわけではない｣ということになるだろう。｢謎の相関を考慮することで、謎の制約条件が発生し、それが、たまたま誤差が縮小する方向に作用した｣に過ぎないかもしれない、という疑念が晴れない。そもそも、量子もつれは、量子アルゴリズムを加速すると主張する論文はある(例えば、[*A-58])が、精度を上げると主張する論文はないと思われる(知らないだけかもしれない。ただし、｢量子もつれは、必ずしも古典システムが達成できる以上の機能を可能にするわけではない(例えば、[*A-65])｣)。
　CNOTゲートは、親関節が制御量子ビットで子関節がターゲット量子ビットである。つまり、親関節の状態によって、子関節に回転ゲートが作用するか否かが決定されるはずである。本論文の場合、与えたエンド･エフェクタの目標座標値が特定の場合にのみ、CNOTゲート機構が、たまたま上手く作用したという可能性は無いだろうか。

【5】追記　
　中国を除いたベースで、一般的に有名なスタートアップは以下であろう：米Figure AI、Boston Dynamics、米Apptronics、米Agility Robotics、米1X Technologies。Boston Dynamicsは、まずグーグルに買収された。グーグルのヒト型ロボット開発撤退に伴い、ソフトバンクが買収したが、ソフトバンクも興味を失い撤退。その後、韓国の現代自動車が買収した。

【0】はじめに　
(0)　露払い
　量子優位性の論争は、血塗られた歴史である。量子優位性を実証したという最初の宣言は、2019年10月23日に発出された。この量子優位性･爆勝宣言byグーグルは、直ぐに否定された。そして、その後同じことが繰り返された(顛末記は、こちらを参照)。知る限りでは、これまで量子優位性の宣言は9件あり、その内、量子アニーリング･マシン(D-Wave)による2件(25年3月、25年４月)が生き残っていると認識している(☞【6】(1))。ゲート方式量子コンピューターによる量子優位性は、ゼロである。
　そういう状況下━ゲート方式量子コンピューターによる量子優位性は、いつになったら現れるんですか？━の2025年夏、量子優位性に関する論文が2本発表された。
(1)　1本目　
　(2段組ながら9頁と短い)1本目の論文は、米IBMと仏Pasqal^🐾1が書いた論文[*A-63](25年7月14日@arXiv)である。同月21日には、IBMが自社ブログ[*A-64]を投稿している。[*A-64]でホワイトペーパーと呼ばれ、実際にそうである[*A-63]は、比喩的に述べると、｢(ゲート方式量子コンピューターによる)量子優位性という金鉱脈は、目の前に有りますよ｣という甘言で構成されている。なお、[*A-63]の対象は、量子計算に限定されている。
🐾1　量子H/W開発スタートアップ。モダリティは、中性原子。24年6月6日、IBMとの提携を発表している。
(2)　2本目　
　(1段組ながら35頁^🐾2と長い)2本目の論文は、米カリフォリニア工科大学(Caltech)他^🐾3の研究者が書いた論文[*A-65](25年8月13日@arXiv,ver2)であり、[*A-63]に比べると、やや高尚であり、包括的である。中身を比喩的に述べると、｢(ゲート方式量子コンピューターによる)量子優位性を探す航海の海図を提供｣している。少し具体的に述べると、表向きには、｢未踏の量子優位性領域は、広大｣である(→必然的に、[*A-65]の対象は、量子計算に限定されていない)と意気っている。裏向き(?)には、｢量子コンピューターは古典コンピューターより”何億倍･何兆倍も速い”^|余談|とかって、そろそろ止めない？｣と囁いている(☞【6】(2))。
🐾2　本文17頁＋付録13頁＋参考文献リスト5頁。
🐾3　米マサチューセッツ工科大学、グーグル(Quantum AI)。Caltechのジョン･プレスキルが著者に名を連ねている。
|余談|　これらは、アーティスト･インフルエンサー･ユーチューバー他の形容に使われるSNS再生回数･数億回、と同じノリである。承認欲求とは違うが、アテンション･エコノミーの悪影響は受けている。

【1】[*A-63]の主張　
　[*A-63]は、以下を主張する：
(0)　2026年末までに、量子優位性の最初の実証について合意に達すると予測する。
(1)　量子優位性への道筋が見えている問題が、3つある。

【2】[*A-65]の主張　
　[*A-65]は、以下を主張する：
(1)　量子優位性を議論するには、3つの新たな視点が必要である。
(2)　量子優位性を定義するには、5つの要件が必要である。
(3)　量子優位性領域には、｢計算上の優位性｣以外の優位性が(豊富に)存在する。

【3】[*A-63]の主張の補足　
(1)　 量子優位性への道筋が見えている問題が、3つある　
1⃣　サンプリング問題(サンプリング･アルゴリズムで解く問題)　
㈠　メイン　
　先走って、量子優位性の要件の一つである予測可能性の視点で述べると、量子優位性を古典シミュレーションで確実に識別することはできないことが、[*A-65]で示されている(☞【4】(2)1⃣)。幸運なことに、サンプリング･ベースのアルゴリズムは、その縛りを逃れることができる。なお、特定のサンプリング問題は、検証可能性をクリアすることが[*A-63]で示されている。
　具体的なサンプリング･ベースのアルゴリズムとして、QAOA(近似的量子最適化アルゴリズム)が取り上げられているが、量子アルゴリズム×最適化問題については、次のような辛辣な意見が述べられている：｢ほとんどの最適化問題において、量子による汎用的な高速化は期待できない。ただし、特定の問題インスタンスにおいては、古典ソルバーよりも優れた解を見つけられる可能性がある｣。
㈡　補記：ランダム回路サンプリング　
　サンプリング･アルゴリズムといっても、｢血塗られた量子優位性の歴史｣の主役であるランダム回路サンプリング(RCS)については、次のような厳しい意見を述べている：｢未だ量子優位性への完全に満足のいく道筋を構成していないと結論付ける｣。さはさりながら、ピーク･ランダム回路に基づく有望なRCSの変種が導入された、として期待も示している。
2⃣　変分問題(変分原理に基づくアルゴリズムで解く問題)　
㈠　メイン　
　先にあげた、”古典シミュレーションでは、確実に識別できない”課題を、 変分問題は次のように回避できる可能性がある：変分アルゴリズムは、厳密解が存在しない場合でも、エネルギー推定値によって(古典的に)近似解を、｢順位付けする｣ことができる。従って量子的に得られた解が、古典的に得られる解よりも低いエネルギーを持つ場合、それは量子優位性の可能性がある。なお、特定の変分問題は、検証可能性をクリアすることが[*A-63]で示されている。
㈡　具体名　
　さらに、量子優位性を実現しそうな具体的なアルゴリズムについても言及されている。IBMが開発したSQD法(サンプルベース量子対角化)と、同じくIBMが開発したサンプルベースのクリロフ量子対角化法(サンプルベースのKQD^{❚補足1❚}＝SKQD)である。サンプリング･ベースのアルゴリズム(⤴1⃣)というところがミソであろう。SQD法については、こちら及びこちらを参照。
3⃣　期待値計算　
　割愛(しても、特に問題はないと思われる)。
❚補足1❚　
　クリロフ量子対角化(Krylov Quantum Diagonalization：KQD)法は、量子コンピューターを使うことで、クリロフ部分空間法の欠点を補ったアルゴリズムである。IBMと東京大学が共同開発した([*A-66]@nature communications、25年6月24日)。クリロフ部分空間法は、(係数行列が疎である場合に用いられる)連立一次方程式の反復解法の一種である。クリロフ部分空間法では係数行列を直接操作しないので、係数行列の疎性が維持できる(疎行列を三角行列に分解すると起きる、フィルインが発生しない)。
　その反面、メモリ･計算量爆発が避けられないという課題がある。この課題を量子コンピューターを使うことで解決した。[*A-65]でspace advantageと呼ばれている量子優位性(☞【4】(3)4⃣参照)の好例と言えるだろう。

(2)　量子優位性の定義　
　[*A-63]では、 量子優位性の定義する要件は2つである。対して、[*A-65]は5つである^🐾4。
🐾4　[*A-65]が量子計算だけを対象としているわけではないため、堅牢性が加わる。そのことを考慮したとしても、[*A-65]の要件は包括的と言えるだろう。
1⃣　 検証可能性　
　量子コンピューターが正しい出力を生成している(信頼できる)ことが確認できる場合を、検証可能と呼んでいる。これは概念的に[*A-65]と同じと思われるが、具体策は異なる。[*A-63]では、まず、計算が信頼できることを保証する普遍的な方法は、計算のすべてのステップが正確に実行されたことを確認すること、とする。そして、これを形式的に実現する方法は、証明されたエラー･バーを用いることだ、とする。そして、このようなエラー･バーを保証する主要な方法は、誤り耐性量子コンピューティングである、とする。これは、古典的に処理したい場面に、量子技術が要請されるという困った状況であり、[*A-65]の予測可能性(☞【4】(2)1⃣)と同じ状況である。[*A-63]では、問題インスタンスによっては、この状況を回避できるという逃げ方をしている。
　一方[*A-65]は、計算が信頼できることを古典的に保証可能という立場である。ただし、その方法は、クリフォード･ゲートからの出力に限定されるのではないかと疑ってる(☞【4】(2)4⃣参照)。クリフォード･ゲートからの出力で十分か否かは、分からない。
2⃣　量子分離　
　[*A-63]では量子分離(原語ではquantum separation)と言う文言が登場している。これは分かり難いが、量子コンピューティングと古典コンピューティングとの間における、アルゴリズム的分離を指しているようである。つまり量子分離とは、古典アルゴリズムの力を借りずに、量子アルゴリズムの力だけで量子優位性を達成するケースを指していると思われる(当然の要請であろう)。そして、｢実質的かつ無条件^🐾5の量子分離が存在するかは不明｣であるが、｢特定環境下では、無条件分離が実証されている｣と記述されている。もっとも、無条件分離が実証されているケースでは、量子と古典との性能差は通常、｢指数関数的ではない｣らしい。
🐾5　実質的＝実社会の問題解決に資する、と言う意味であろう。無条件＝何らかの仮定を含まない、という意味である。何らかの仮定には、証明されていない仮定も含まれる。

(3)　為参考：量子優位性を実現するための3要素　
　当たり前でしょ的な感じもするが念の為、[*A-63]の言い分を簡単に整理した：①量子回路を正確に実行するための方法(量子誤り訂正、量子誤り緩和、量子誤り検出)、②古典コンピューターとの連携(で量子優位性は実現する)→※、③量子プロセッサ(いわゆるQPU)。
※　②は上記(2)2⃣量子分離と矛盾するような気もする。

【4】[*A-65]の主張の補足　
(1)　量子優位性を議論するには、3つの新たな視点が必要である。
0⃣　概要　
　[*A-65]は次のように述べる：これまで、数学的証明と複雑性理論に基づく議論により、量子優位性は確立されてきた。しかし、古典コンピューターの歴史を参考にするならば、この枠組みだけで量子優位性の全体像を把握することはできないであろう。━というわけで、前向きな･超ポジティブ･斜め上(?)の新しい3つの視点が提案されている：経験的量子優位性、概念的量子優位性、予測不可能な量子優位性(!)である。一番インパクトが大きな視点は、予測不可能な量子優位性であろう。
1⃣　予測不可能な量子優位性　
　 予測不可能な量子優位性とは、不思議な言い回しであるが、次のような説明をすればモヤモヤが消えるだろう。[*A-65]は(付録Dにて)、𝖡𝖯𝖯≠𝖡𝖰𝖯^🐾6という仮説を認めると、量子優位性の識別は古典的には困難であることを示している(☞詳細は、下記(2)1⃣を参照)。言葉を替えると、古典的な技術では真の量子優位性と疑似量子優位性を確実に区別することができない。これだと、ネガティブな主張に聞こえてしまうが、これを次のようにポジティブ変換しよう：量子優位性の存在領域は、古典コンピュータの予測能力を超えて存在している。
　つまり、人類が現状有している技術の範囲では、量子優位性のほとんどは、原理的に見つけられない。故に、量子優位性が見つかっていないだけである。実は、未踏の広大な領域に豊富に存在している。と[*A-65]は考えている。議論のあるところかもしれない。
🐾6　𝖡𝖯𝖯≠𝖡𝖰𝖯は、量子コンピューターは古典コンピューターでは解けない問題を効率的に解くことができると主張している。この仮定は十分な証拠によって裏付けられているものの、あくまで仮説に過ぎない。事実上、主張されている全ての計算量子優位性の基盤となっている。
2⃣　経験的量子優位性　
　メジャーとは言えないが、それほど目新しいテーマではない。経験的(empirical)とは、理論的の対義語として使われている。この場合の理論とは、言わずもがな複雑性理論である。複雑性理論で量子優位性を議論する場合、オーダーで議論する。つまりオーダーが同じだと、｢優位性なし｣となってしまう。しかし、実務的な立場からは、これはあまりに乱暴、という主張である。つまり、｢オーダーは同じだけれども、定数倍は違う｣という状況で定数が十分に大きい場合、実際の計算時間は、実務に対してインパクトを持つよ、という主張である^🐾7(と理解している)。
　[*A-65]では、もう1つの例が上げられている。それは、同程度に速い古典アルゴリズムの発見に、長い時間を要した場合、トータルで見ると量子に優位性が発現していると言って良いのでは？という主張である。つまり、同程度に速い古典アルゴリズムであれば、その発見に長い時間をかけるのはムダだから止めましょう、という意見である。これは、議論の余地のある意見であろう。
🐾7　実際の計算時間(wall clock time)という舞台だと、別の意味でややこしくなる。つまり、エンドツーエンドで考えると、データ･ローディングの時間も加味しなくてはならない。よく言われるように、そこで指数関数的な時間を要すれば、定数倍などは吹き飛ぶ。
3⃣　概念的量子優位性
　これは、やや高尚というか哲学的である。曰く(disagreeというわけでは、全くないが)、シンプルisベスト・本質はシンプルである、といった物理学的な世界観(哲学)がベースにある(と思われる)。 まず、｢量子的なソリューションは概念的に単純であり、問​​題を理解するためのより自然な枠組みを提供する可能性がある｣との主張を措く。そして、｢シンプルな概念的枠組みは、しばしばより深い根底にある構造を反映しており、研究者を新たな理論的洞察や技術的方向性へと導く可能性がある｣と続ける。
　つまり概念的量子優位性には、量子の枠組みをH/W及びS/Wに使うことで、新しい物理学が開拓される(少なくとも開拓が加速される)可能性がある、という期待が反映されている(と思われる)。

(2)　量子優位性を定義するには、5つの要件が必要である。
0⃣　露払い　
　5つの要件とは、予測可能性、汎用性、堅牢性、検証可能性、有用性である。初っ端の予測可能性が、いきなり、(1)1⃣の 予測不可能な量子優位性とバッティングするところが面白い。なお、[*A-65]は5つの要件に対して、次のような問いを立てている：予測可能性、汎用性、堅牢性、検証可能性、有用性を同時に満たす量子優位性とは、どのようなものだろうか？　5つの要件をすべて満たす量子優位性を発見するための新たなアプローチを開発することは可能だろうか？
1⃣　予測可能性　
　量子優位性に予測可能性(原語では、predictability)があるとは、量子優位性を、古典的技術で確実に識別できる、ことを意味している。古典的技術とは、古典物理学(古典力学、熱力学、古典電磁気学)をベースとした技術である。例えば、古典コンピューターを使った古典シミュレーションが、今の文脈における｢古典的技術｣の代表例となるだろう。
　しかし残念ながら、予測可能性＝古典シミュレーション可能性、とは言い替えられない。[*A-65]は(付録Dにて)、𝖡𝖯𝖯≠𝖡𝖰𝖯という仮説を認めると、量子優位性の識別は古典的には困難であることを示した。このため、｢予測可能性｣で表明したいことは、𝖡𝖯𝖯≠𝖡𝖰𝖯 という計算量理論上の仮説を使わずに(古典シミュレーションを使わずに)例えば、｢物理原理に着想を得たような、量子優位性を予測できる新たな古典的技術を開発｣し、｢予測可能な量子優位性を見つけて行こう｣という行動指針と思われる。なお[*A-65]では、｢量子優位性を厳密に予測･定量化する能力は、量子優位性そのものと同じくらい変革をもたらす可能性がある｣と述べられている。
　もっとも、上記は理想的な(あるいは完全な)フレームワークを作りたい、という意見である。【3】(1)1⃣や2⃣で示したように、問題インスタンスによっては、古典シミュレーションが不可能でも、量子優位性の識別は可能である。
2⃣　汎用性　
　量子優位性に汎用性(原語ではtypicality)があるとは、レアでない、ということである。[*A-65]は、｢稀にしか発生しない病的な特定事例に限定されるのではなく、実用上重要な事例の多くに(量子優位性が)現れる｣ことに価値がある、と考える。つまり、病的な特定事例に限定される汎用的でない量子優位性は無視しよう、との主張である。
3⃣　堅牢性　
　量子優位性に堅牢性(原語ではrobustness)があるとは、理想的な理論的仮定からの逸脱^🐾8にもかかわらず、量子優位性が持続する場合を指す。堅牢性の議論は、量子計算、量子センシング、量子機械学習のそれぞれで、様相が異なる。先走って答えを言えば、量子機械学習のみ、堅牢性が未解決である。
🐾8　ノイズに加えて、｢ハードウェア、利用可能なリソース、入力データなどの不完全性｣を含む。
㈠　量子計算　
　量子計算には、有名な”しきい値定理”が存在する。つまり、量子ゲートの物理誤り率がしきい値以下である場合に限り、適当な量子誤り訂正プロトコルを適用すれば、｢理想的な理論的仮定からの逸脱｣があったとしても、量子優位性は持続する。従って、量子計算の量子優位性には、堅牢性が備わっている。
㈡　量子センシング　
　驚くべきことに、量子計算に備わっている堅牢性は、量子センシングには存在しない。一般的なノイズが存在する場合、量子誤り訂正プロトコルを適用したとしても、量子センシングで量子優位性は実現できない(らしい!)。量子優位性を維持できる特殊なケースは、(3)3⃣㈡を参照。
㈢　量子機械学習　
　一部の量子機械学習の量子優位性は、現実的なノイズ条件下でも持続することが証明されている(らしい)が、他の多くの量子機械学習における量子優位性の堅牢性は、未証明らしい。
4⃣　検証可能性　
㈠　深遠なる問い　
　ここで述べられている検証可能性(原語ではverifiability)は、一般的な用語としての検証可能性、あるいは[*A-63]で言及されている検証可能性とは、趣がやや異なる。[*A-65]は、高度に複雑なエンタングルメントが支配的な領域で量子力学が妥当であり続けると信頼できるのか？という、やや深遠な問いを投げかけている。実は、量子力学に対する信頼は、主にエンタングルメントが限られた比較的単純な物理系における実験に基づいている。数千個の粒子が複雑な量子相関を維持する物理系において、量子力学は検証されていない。高度に複雑で大規模なエンタングルメントの領域で(われわれが知っている)量子力学は、異なる挙動を示す可能性がある。とは言え、とりえず、この深遠な問いは無視されている。
㈡　定義　
　ここで検証可能性の定義を示す：量子デバイスが正しい出力を生成している(信頼できる)ことを、効率的に確認できる場合、量子優位性は検証可能であると言う。言わずもがなであるが、量子技術の文脈で効率的とは、古典コンピューターを使って多項式オーバーヘッドでシミュレート可能という意味である。
㈢　量子計算に関する検証可能性　
　不思議なことに、量子コンピューター(量子計算機)を、｢信頼できる測定装置として識別できる｣測定プロトコルを構築することが可能である[*A-67]。この測定プロトコルを使って、量子コンピューターが正しい出力を生成しているか否か？を検証する作業は、古典コンピューターだけで実行できる^{❚補足2❚}。ただし、この(測定プロトコルを含む検証作業全体に渡る)検証プロトコルは、耐量子暗号の暗号プリミティブ^🐾9である、｢LWE問題^🐾10は量子コンピューターでも多項式時間で解くことが困難である｣という仮説に基づいている。
🐾9　暗号の解読困難性(安全性)を保証する数学的背景(数学理論とか数論上の問題など)を、暗号学の文脈では、暗号プリミティブと呼ぶ。半導体分野の用語に被れて、IPコアと呼ばれることもある。
🐾10　Learning With Errors問題。機械学習理論において、たまたま発見された問題で、具体的には、｢故意に誤差を付加した多元連立一次方程式を解く問題｣である。LWE問題の解読困難性は、米NISTが定めた暗号ML-KEM(旧Crystals-Kyber)が耐量子であることの理論的前提でもある。
㈣　量子計算以外の検出可能性　
　[*A-65]は、以下のように述べている：量子計算には一般的な検証スキームが存在する。一方、量子センシングにおいては、検証は間接的な証拠や統計的な整合性チェックに依存することが多い。量子機械学習においては、量子優位性の検証は依然として困難である。
❚補足2❚　
　古典コンピューターだけで実行できる理由は、クリフォード･ゲートの出力のみを使って、正しい出力を生成しているか否か？を検証しているからと思われる。仮にそうだとしたら、クリフォード･ゲートの出力のみで、良いのだろうか？
　なお、当該検証プロトコルの世界は(おそらく)、量子回路を古典アルゴリズムが効率的にシミュレートしても良い世界なので、𝖡𝖯𝖯≠𝖡𝖰𝖯の制約は受けないと思われる。
5⃣　有用性　
　量子優位性に有用性(原語ではusefulness)があるとは、次のように定義されている：重要な応用のための効果的な手法を求めるユーザー、そして、その基盤となる技術が古典的か量子的かを問わないユーザーにとって、その優位性が実用的な価値を提供する場合を指す。
　なお有用の中身について、[*A-65]は、次のように述べている：最も影響力のある量子優位性は、理論上の速度向上が最も顕著なものではなく、量子アプローチが質的に新しい能力や知見をもたらす応用分野である可能性もある。

(3)　量子優位性領域には、｢計算上の優位性｣以外の優位性が(豊富に)存在する。
　 ザックリ言うと[*A-65]は、｢未踏の量子優位性領域は、広大である｣と主張している論文である。以下、具体的に見てみよう。なお、現在認識されている量子優位性は、証明されていない計算量仮定に基づくものもあれば、物理法則そのものによって保証されているものがある。
0⃣　計算上の量子優位性　
㈠　メイン　
　計算上の量子優位性は、最も広く研究されており、計算問題のより高速な解を約束するアルゴリズムを特徴としている。しかし、この領域は、真の優位性と微妙な錯覚が共存する複雑な領域であり、優位性の基盤は計算量に関する仮定に基づいている。[*A-65]は、｢計算上の量子優位性には、絶え間ない監視が必要である(期待が薄い)｣と結論している。
㈡　補記：データの威力半端ねぇ？　
　いくつかのトピックスが取り上げららえているが、本稿では、Power of data(データの威力半端ねぇ)のみを取り上げる。これは、次のようなことを指している：量子シミュレーション、量子センサー、量子実験が、古典的には効率的に生成できないデータを生成する場合に、そのようなデータで学習した古典機械学習アルゴリズムは、古典データで学習した古典アルゴリズムの到達範囲を超える。すなわち、量子データさえあれば、量子計算を必要とせずに量子現象を近似できるケースが存在し得る。言葉を替えると、計算上の量子優位性の一部は壊れることになる。ただし𝖡𝖯𝖯≠𝖡𝖰𝖯の仮定下では、すべての量子データを古典的にシミュレートすることはできない。その場合は、量子コンピューターと古典コンピューターを連携させることで、対応可能となる。やはり、計算上の量子優位性の一部は壊れることになるだろう。
1⃣　量子機械学習上の量子優位性　
㈠　メイン　
　量子機械学習における量子優位性は(計算上の量子優位性とは異なり)、証明されていない複雑性理論上の仮定に依存するのではなく、物理的現実そのものの量子的な性質から生じることが多い。ただそれは、量子機械学習の対象を物理系に限定した場合に限り(未証明である複雑性理論上の仮定に依存せずに)、量子優位性が発現することを意味しているに過ぎないかもしれない。それ自体驚くに値しないが、(マーケティング応用とかSNS分析のような)実社会を対象とするアプリケーションで量子優位性を期待している人々にとっては、やや失望を与えるかもしれない。
㈡　補記：指数加速　
　量子学習エージェントを多体系物理システムおよびダイナミクスの研究に適用した場合、指数関数的な量子優位性が発現し得る(らしい)。正確には、古典アプローチよりも指数関数的に少ない実験回数で学習可能である(らしい)。[*A-65]は、｢最も革新的な機会は、量子センサーと量子コンピューターをシームレスに統合する量子学習エージェントから生まれるかもしれない｣と述べている。
2⃣　量子センシング上の優位性　
㈠　メイン　
　量子センシングにおける量子優位性も(計算上の量子優位性とは異なり)、証明されていない複雑性理論上の仮定に依存するのではなく、物理的対象の量子的な性質から生じることが多い。センシングは、対象を物理的対象に限定しても大きな問題はないだろう。その代わり、理論的な限界がある(☞下記㈡参照)。
　量子コンピューターを量子コンピューティング強化センシングと呼ばれるフレームワークで、量子センサーと統合することで、古典コンピューターのみで制御される量子センサーよりもかなり高速に古典場の特性を学習できることが実証されている。具体的には、電磁信号や重力波などのセンシングに適用した場合、量子エージェントは2次多項式を超える高速化を達成できる。
㈡　補記：理論的な限界　
　Hamiltonian-not-in-Lindbladian-span[*A-68]基準によれば、量子センシングにおいて量子優位性がノイズ存在下で存続できるのは、シグナルとノイズが演算子レベルで区別できる場合のみである。
3⃣　金融分野における量子優位性　
㈠　偽造不可能プロトコル　
　量子力学における量子複製不可能定理(ノー･クローニング定理、クローン禁止定理)は、本質的にコピーに対する保護機能を備えたオブジェクトの作成を可能にし、古典物理学では不可能だった新しい種類のアプリケーションの可能性を切り開く。[*A-65]では、量子マネーが例示されている。量子マネーは、量子状態を用いて効率的に検証可能である一方、完全に複製できないシリアル番号を符号化することで、偽造不可能な通貨を作成することを目指している。
㈡　量子もつれと戦略ゲーム　
　[*A-65]で、掲題の事例として上げられている論文については、こちらを参照。
4⃣　情報量に関する量子優位性^🐾11　
㈠　メイン　
　特定の計算タスクにおいて、量子状態は、指数関数的に圧縮された古典データとしての役目を果たすことができる。一般的にはホレボー(Holevo)限界^{❚補足3❚}により、小さな量子メモリから指数関数的な数の古典ビットを抽出することは、禁じられている。ただし、特定の計算タスクは、(古典データを指数的に圧縮した)量子データに対して、データ再構成を完全に行うことなく実行可能である。つまり量子には、情報量に関して優位性が存在する。
　また、古典アルゴリズムは、各データ要素が到着するたびに、どの情報を保持するかについて不可逆的な決定を下す必要がある。一方、量子アルゴリズムは、この不可逆な決定を、より多くの情報が得られるまで効果的に延期することができる。つまり量子には、情報量に関して優位性が存在する。
🐾11　原語では、space advantage。なので、思い切り意訳。spaceは、情報を記憶するメモリ空間を意味しているという理解。
👉　量子情報超越性(quantum information supremacy)とのアナロジーから言うと、それほど悪くない和訳と言えなくもない。
㈡　補記：制限　
　情報量に関する量子優位性には重要な限界がある。通常、入力サイズがメモリ容量を大幅に超える場合にのみ適用される。さらに、量子システムに大量のデータを入力するにはコストがかかる可能性があり、実行される計算タスクは、ホレボー限界と互換性がなければならない。
㈢　実例　
　クリロフ量子対角化法は、量子技術(量子コンピューター)を使って、クリロフ部分空間法のメモリ･計算量爆発問題を解消した。情報量に関する量子優位性が発現した好例と言えるであろう。
❚補足3❚　
　情報伝送効率(一度に送れる情報量)の限界を意味する。パルス(レター状態)を個別測定して復号する戦略における通信路容量を、シャノン限界と呼ぶ。これに対して、レター状態を一括測定して復号する戦略における通信路容量を、ホレボー限界(あるいは、ホレボー･シューマッハー･ウェストモーランド限界)と呼ぶ。通信路容量＝最大伝送情報量であり、ホレボー限界≥シャノン限界、である。

【5】考察･感想　
　量子優位性の定義【3】(2)1⃣及び2⃣並びに【4】(2)1⃣及び4⃣。新しい視点【4】(1)1⃣,2⃣及び3⃣。計算上の量子優位性【4】(3)0⃣。どれも厳しい、という印象を持つのではないだろうか。視点を変えると、量子優位性の実現が如何に難しいか納得できる。そして、量子優位性は、現在の想像を超えた領域で姿を表すだろうというのは、怪しく(妖しく)魅力的ではある。

【6】付け足し　
(1)　(D-Waveの量子アニーリング･マシンによる)量子優位性として生き残っている2件：横磁場イジングモデルの量子シミュレーション(25年3月12日@Science[*A-69])、最適化計算(25年4月23日@Physical Review Letters[*A-70])。[*A-69]は、部分的な反論がなされている(こちらを参照)。

(2)　潘建偉のグループは、量子計算機が古典計算機より、10⁵⁴倍速いと主張する論文[*A-71]を発表した(25年8月24日@arXiv)。量子計算機は、ガウス･ボソン･サンプリング(GBS)専用機｢九章｣の4代目。古典計算機は、米ローレンスリバモア国立研究所にて稼働している世界最速スパコン｢エル･キャピタン｣(as of 25年6月のTOP500)。九章は、20年に量子(計算)優位性を主張したが、およそ2年半後、テンソルネットワーク(正確には、行列積状態(MPS))を使用して、GBSを古典的に効率的にシミュレートすることで反論された。今回、エルキャピタンを使っても、シミュレーションに必要なMPSの構築に10⁴²年かかる、と主張している。一方、九章4.0は25.6μ秒しかかからないと主張している。
　[*A-65]の定義に従えば[*A-71]の成果は、汎用性と有用性に欠けるということになるだろう。こういうことは、もうそろそろ止めましょう、ということになる。

‖はじめに‖　
　独ベルリン自由大学のJens Eisertと米カルテックのJohn Preskillは25年10月22日、Mind the gaps: The fraught road to quantum advantageと題する論文[*A-75]をarXivにて公開した。現在のNISQマシンと、近い将来に登場が期待されるFASQ^🐾1マシンとの間に、 存在するギャップに関するレビュー論文という趣である。以下にあげる、当該ギャップにまつわるテーマ4つが特出しされている：〖1〗量子誤り緩和、〖2〗量子誤り訂正及びモダリティ、〖3〗量子アルゴリズム、〖4〗量子シミュレーション。それぞれについて、箇条書き的に簡単に整理した。
🐾1　 Fault-tolerant Application-Scale。誤り耐性を備えた量子コンピューターでなければ解決できない規模感のアプリケーションに対応できる量子コンピューターのクラス、という意味(だという理解)。なお、SCaleがSQaleとされている。

〖0〗全体感　
❑　実用的で経済的に実現可能な量子計算はまだ達成されておらず、それがいつ実現するのかも明らかではない。NISQからFASQへの道のりは、おそらく困難で、費用がかさみ、長期にわたるものとなるだろう。
❑　将来の幅広い用途に対応できる量子プロセッサは、現在盛んに研究されているものとは異なるハードウェア方式やアーキテクチャ原理に基づいている可能性がある。
❑　量子コンピュータが、最適化問題及び機械学習に対して、価値をもたらすことが期待されている。しかし、その実現は、これまでのところ困難である。
❑　量子コンピュータがシミュレーション分野で、自然科学研究に価値をもたらす時間軸は近いだろう。一方で、社会的に価値をもたらす時間軸は近くないだろう(→莫大な量子リソースが必要なため)。
❑　フォン･ノイマンが高速電子計算機の価値について考察したケースと同様に、我々は、｢量子コンピューターの最も影響力のある、将来の応用を予見することはできない｣。➡目に見える形で、量子優位性が現れていないからといって、量子コンピューターを見限らないで！

〖1〗量子誤り緩和(QEM)　
❑　QEMは、非常に大規模な回路には適用できない。しかし、量子誤り訂正(QEC)が成熟しても、QEMは誤り耐性プラットフォームが到達できる回路サイズを拡大したり、サンプリング･オーバーヘッドの増加を犠牲にして誤り訂正のオーバーヘッドを削減したり、回路コンパイル誤りを軽減したりするために、引き続き重要な役割を果たすだろう。
❑　｢幅100、深さ100｣＝1万ゲート程度の回路でも、非平衡状態にある多体量子系のダイナミクスに関する科学的に価値のある知見を得られる可能性がある。1万ゲート程度なら、QEMで対応できる。

〖2〗量子誤り訂正(QEC)及びモダリティ　
━　QEC　━━━━━━━
❑　グーグルは表面符号で、符号距離スケーリングを実証した(→Willow量子チップ)。ただし、表面符号には、符号化率が低いという短所がある。　
❑　符号化率が高い符号として、｢IBMのBB符号｣を始めとする量子低密度パリティチェック(qLDPC)符号がある。ただし、これらの高符号化率符号のエラーシンドロームを測定するには、幾何学的に非局所的な物理操作^🐾2が必要になる、という課題がある。
❑　猫量子ビットは、複雑なハードウェアを必要とするが、QECのオーバーヘッド･コストを削減できる可能性がある。
❑　デュアルレール符号化の利点は、量子誤りを直接検出できるため、誤り訂正タスクが簡素化されることである。
❑　量子コンピューティングの規模が拡大するにつれて、より優れた復号方法とより高速な古典的な処理が必要になるだろう。
🐾2　幾何学的に非局所的な物理操作は、中性原子方式やトラップイオン方式とは親和性高いが、超伝導方式とは親和性が低い。
━　モダリティ^🐾3　━━━━━━━
❑　中性原子方式及びトラップイオン方式では、誤り耐性回路の目覚ましい実証が達成されている。しかし、これらの実証は数ラウンドのエラーシンドローム測定に限定されており、低い論理誤り率を達成するために古典的事後選択が用いられている。つまり、量子誤りが検出された場合は回路実行が破棄されるというスキームであり、大規模な回路には適用できない。
❑　超伝導量子ビットの多くは、トランズモンに基づいている。それは、構造が単純だからである。しかしQECの莫大なオーバーヘッド･コストを鑑みると、構造を複雑にしても、物理誤り率を下げるという選択肢も有り得る。例えば、フラクソニウム量子ビットがあげられる。
🐾3　[*A-75]では、トラップイオン・超伝導・中性原子の3つが主要なモダリティとして、ピックアップされている。光と(シリコン)スピンは、次点という扱い。

〖3〗量子アルゴリズム
❑　不毛な台地現象等により、変分量子アルゴリズムが量子優位性をもたらすことには、疑問が呈されている。ただし、変分探索の初期パラメータを戦略的に選択すること(いわゆる、ウォームスタート)により、性能を大幅に向上できる可能性はある。
❑　非常に大規模なインスタンスに対してのみ有効なグローバー･アルゴリズムは、長期的には価値があるかもしれないが、おそらく今後『数十年は実現しない』だろう。
❑　量子コンピュータがNP困難問題の最悪ケースのインスタンスに対する厳密解を効率的に見つけることは期待できない。ただし、古典コンピュータよりも優れた近似解を見つけたり、優れた近似解を見つけるための探索を高速化したりできる可能性がある。
❑　復号量子干渉法(DQI)のような、量子優位性を探求するための新しいパラダイムが登場している^🐾4。DQIは量子フーリエ変換によって、古典的に困難と思われる問題を、古典的に容易に解ける復号問題にマッピングする。DQIを古典的にシミュレートすることは困難であることが示されている。同時に、非構造化組合せ最適化問題において、DQIは量子的な優位性をもたらさないことも示されている。
❑　エンド･ツー･エンドの機械学習タスクにおける量子コンピューティングの有用な優位性の可能性は、依然としてほとんど解明されていない。いくつかの人為的例では、高速化が実証されているが、大規模なインスタンス群に対して、量子優位性を確立することは依然として困難である。
❑　線形偏微分方程式を高速に解く量子アルゴリズムが知られている。ただし、エンド･ツー･エンドで高速化するには、｢適切な境界条件の符号化、効果的な事前処理法の適用、出力状態の測定から有用な情報を抽出する｣など、解決すべき様々な課題が残されている。また、非線形および確率微分方程式への拡張も、途上である。
🐾4　非時間順序相関関数(OTOC)も取り上げられている。OTOCについては、こちらを参照。

〖4〗量子シミュレーション
❑　量子コンピュータ上で局所ハミルトニアンの基底状態を準備し、その状態における観測量を測定するための、効率的な量子アルゴリズムが存在する。ただし、当該アルゴリズムは、基底状態と大きな重なりを持つ入力状態を準備できる場合にのみ、効率性が保証される。そして、その場合が古典的に困難であるかは、証明されていない。つまり、量子シミュレーションでも量子優位性が無条件で成立するわけではない。
❑　平衡状態から大きく離れた系のハミルトニアン時間発展は、量子優位性を示す有望な分野である。ただし、ここでも、量子優位性が証明されているわけではない。
❑　平衡状態および非平衡状態の両方において、高度に絡み合った新しい物質相を発見し、他の計算手法では到達できない強結合量子系の特性を探求できると期待される。対象分野としては、まず凝縮系物理、次に化学、そして最終的には高エネルギー物理学、さらには量子重力理論において大きな影響があると予想される。
❑　科学的発見のためのツールとしての量子シミュレーションの可能性については確実性が高い。一方、産業応用における有用性を予測することは困難である。

【0】はじめに
｜概要｜　出願において保留中で却下された特許請求項(クレーム)の審査官による拒絶に対して、特許出願人が控訴し、米国特許商標庁^🐾1(United States Patent and Trademark Office：USPTO)特許審査部^🐾2(あるいは、特許審判部。Patent Trial and Appeal Board：PTAB)が審査した。PTABは、審査官が｢抽象的で特許不適格なアイデア｣として却下した判断を覆した(25年2月11日)[＊N-1]。これを、以下では、｢本決定｣と呼ぶ。本決定にかかる特許を、以下、｢本特許｣と呼ぶ。
｜背景｜　日本の特許法第２条第１項は発明を、｢自然法則を利用した技術的思想の創作のうち高度のもの｣と定義する。一方で、特許･実用新案審査基準^🐾3『第Ⅲ部特許要件　第1章発明該当性及び産業上の利用可能性(特許法第 29 条第 1 項柱書)　2. 発明該当性の要件についての判断　2.1 ｢発明｣に該当しないものの類型』によれば、自然法則それ自体(2.1.1 自然法則自体)、あるいは自然法則を利用していないもの(同2.1.4 自然法則を利用していないもの)は、特許法上の発明には該当しない。自然法則を利用していないものには、｢数学上の公式｣が含まれる。
　米国では、特許法第101条が、特許を取得できるものを規定している。そして(判例法主義である米国の)最高裁は、第101条の”暗黙の例外”として、｢自然法則、自然現象｣及び｢抽象的なアイデア(の一部)｣は、特許を取得できないと解釈してきた。抽象的で特許不適格なアイデアに、数式が含まれる。^🐾4
🐾1　米国における特許及び商標の権利付与を所掌する。合衆国連邦政府商務省に属する。
🐾2　PTABは、USPTO内の法廷である。特許審査官による拒絶を一方的控訴として再審査し、第三者が提起した発行済み特許の特許性疑問をAIA審判と呼ばれる手続きで決定する。AIAとは、米国特許改正法(あるいは、リーヒー･スミス･米国発明法。America Invents Act)である。出典：https://www.uspto.gov/patents/ptab/about-ptab-jp　
🐾3　https://www.jpo.go.jp/system/laws/rule/guideline/patent/tukujitu_kijun/document/index/all.pdf
🐾4　1978年の判決で確立されたらしい。

【1】本決定の概要説明
0⃣　特許出願人(発明者)の説明　
　発明者は(当時)、米Zapata Computing Inc.(以下、Zapata)のCTO(最高技術責任者)であったYudong Cao。米ハーバード大学からスピンアウトした量子ソフトウェア･スタートアップとして、2017年に創業したZapataは、代表的な量子古典ハイブリッド･アルゴリズムであるVQE(変分量子固有値ソルバー法)の考案者アラン・アスプル=グジック(当時、ハーバード大学教授)が創業に携わった有望スタートアップであった。｢生成モデルが、量子力学の実用的な優位性をもたらす最も有望な手段であることが明らかになった｣と主張し、量子機械学習に主戦場と定めた。最終的には、生成AIの会社を標榜した(あるいは漂流した？)。
　24年4月NASDAQにSPAC上場したZapataは、24年10月に事業停止している。従って、控訴人は、(ZapataのIPを継承したのであろう)Blueshift IP LLCという企業である。
1⃣　本特許の概要説明
　Zapataは、線形代数方程式(連立一次方程式)を量子コンピューターで解くアルゴリズムについて、特許[*N-2]を出願した。ここで言う量子コンピューターとは、いわゆるNISQ(ノイズの多い量子コンピューター)であり、アルゴリズムは変分量子アルゴリズムである。つまり、代数問題を最適化問題に変換して求解するアルゴリズムである。最適化は、コスト関数(目的関数)を最小化することであり、パラメータを操作することで、コスト関数を最小化するという”立て付け”にする(詳細は【3】参照)。
❑　コスト関数を構成するためには、(自明で準備が容易な)初期状態から、適当な量子状態を準備する必要がある。
❑　パラメータは、パラメータ付き量子回路(業界用語では、アンザッツと呼ばれる)に実装される。パラメータ操作は、古典コンピューターで行う。
2⃣　争いについての概要説明
　争いは、２つある：❶量子状態の準備が、｢抽象的で特許不適格なアイデア｣か否か。❷特許明細書におけるコスト関数の記載に不備があるか否か(記載要件)。

【2】本決定の詳細　
(0)　全体像　
　【1】2⃣❶の争点により、審査官に却下(拒絶)された特許請求項は、1～15および17～31である。本決定は請求項1が、 ｢抽象的で特許不適格なアイデアではない｣と判示することで、請求項1の却下を取り消している。同じ理由で、請求項2–15および 17–31の却下も取り消している→下記(1)。
　【1】2⃣❷の争点により、審査官に却下(拒絶)された特許請求項は、特許請求項1～10、13～15、17～26および 29～31である→下記(2)。

(1)　量子状態の準備が、｢抽象的で特許不適格なアイデア｣か否か　
0⃣　 抽象的で特許不適格なアイデア、抽象的ではあるが特許適格と判断されたアイデア
　【0】にて既述の通り、米最高裁は、米特許法第101条の”暗黙の例外”として、｢自然法則、自然現象｣及び｢抽象的なアイデア｣は、特許を取得できないと解釈してきた。抽象的で特許不適格とされたアイデアには、基本的な経済慣行、数式、および精神的プロセスなどの人間の活動を組織化する特定の方法が含まれる。
　一方、抽象的ではあるが特許適格と判断されたアイデアには、｢ゴム製品の成形｣などの物理的および化学的プロセス、｢なめし、染色、防水布の製造、インドゴムの加硫、鉱石の精錬｣、｢小麦粉の製造｣が含まれる。
1⃣　2段階フレームワーク　
　米最高裁は、特許請求項が、除外カテゴリ(＝自然法則、自然現象及び抽象的なアイデア)に該当するかどうかを判断する際には、 判例で確立された2段階のフレームワークに従う。
　まず、特許請求項が｢対象としている｣概念を決定する。特許請求項が、抽象的なアイデアに｢向けられている｣場合、特許請求項に、抽象的なアイデアを特許適格なアプリケーションに｢変換する｣のに十分な『発明概念』(追加要素)が含まれているかどうかを判断する。
2⃣　審査官の主張　
　量子状態を準備するという『追加要素』に関して、審査官は次のように判断している：
　量子コンピューター上での量子状態の準備は、抽象的なアイデアを実行する際に使用する特定のタイプまたはソースのデータを収集することの記述である。これは、抽象的なアイデアを特定の使用分野または技術環境に限定する試みであり、抽象的なアイデアを実際のアプリケーションに統合したり、抽象的なアイデアを大幅に超えるものにはならない。
3⃣　PTABの主張　
　PTABは、控訴人の主張：｢量子状態を準備するという『追加要素』は、発明の焦点を表しており、記述された抽象的なアイデアを実際のアプリケーションに統合している｣に同意している。そして、｢追加要素は、数学的関係の抽象的なアイデアを、回路の深さが限られているNISQで線形方程式を実際に解くという実際のアプリケーションに統合している。これは技術の改善である｣と判示する。
　さらに、次のように述べている：｢われわれ(PTAB)の主張は、量子コンピューターを使用して線形方程式を解くことができないという従来技術の欠陥と、古典と量子の両方を含むハイブリッドシステムを使用して、線形方程式を解くという本発明の技術改善について記述した明細書によって裏付けられている｣。

(2)　記載要件：特許明細書におけるコスト関数の記載　
1⃣　審査官の主張　
　審査官によると、公開された明細書には、使用できる特定のコスト関数が記載されている。明細書には、他のコスト関数が使用できるという主張以外に、他のコスト関数については何も記載されていない。しかし、明細書は、明細書に具体的に記載されたもの以外に、特許請求項通りに機能するコスト関数を発明者が所有していたという結論を裏付けるものではない。同様に、明細書には、特定された特定の形式のいずれかに従わないコスト関数の生成についても何も記載されていない。
　従って、審査官は、｢明細書には、2種類のコスト関数しか開示されていない｣と判定する。つまり、特許請求項は、コスト関数の全範囲について書面による説明を提供していないとして拒絶された。
2⃣　PTABによる主張の前提　
　米特許法112条(a)は、以下のように定める：明細書には、｢発明およびその製造および使用の方法とプロセスについて、それが関係する、またはそれが最も密接に関連する技術分野の熟練者がそれを製造および使用できるように、完全、明確、簡潔、かつ正確な言葉で記述し、発明者または共同発明者が発明を実施するために想定する最良の方法を記載するものとする｣→｢記載要件｣。
　この｢記載要件｣を満たすには、開示によって、出願日時点で控訴人(＝発明者)が請求された発明を所有していたことが、熟練した技術者に合理的に伝わらなければならない。具体的には、明細書は｢当業者が、特許請求されている発明を、発明したことを明らかに認識できる｣ものでなければならず、テストでは、当業者の観点から明細書の隅々まで客観的に調査する必要がある。その調査に基づいて、明細書には、その熟練した技術者が理解できる発明が記載され、発明者が特許請求されている発明を、実際に発明したことを示す必要がある→｢説明要件｣。
　(書面による)｢説明要件｣を満たすために必要な詳細のレベルは、特許請求の性質と範囲、および関連する技術の複雑さと予測可能性によって異なる。一般的な特許請求項は、開示の適切性を評価するためのいくつかの要素を示しており、｢特定の分野における既存の知識、先行技術の範囲と内容、科学または技術の成熟度、および問題の側面の予測可能性｣が含まれている。
3⃣　PTABの主張　
　我々(PTAB)は、明細書が、出願日時点で、控訴人(発明者)が、特許請求された発明を所有していたことを、熟練技術者に合理的に伝えているという控訴人の意見に同意する。特に、明細書の一部である特許請求項1(☞【3】参照)は、(本決定にかかる)コスト関数について記載している。さらに明細書は、具体的なコスト関数の実装例を提供しており、｢熟練した技術者が、理解できる発明を説明｣している。
　審査官の｢明細書には、2種類のコスト関数しか開示されていない｣という判断は、記載要件ではなく、実施可能性要件に向けられているように思われる。さらに、明細書は「発明者がコスト関数をどのように生成することを意図したか、を示していない｣という審査官の主張は説得力がない。審査官は、明細書に、コスト関数の具体的な例が示されていることを認めている。
　審査官は判例(Vasudevan Software, Inc. v. MicroStrategy, Inc., 2015)を引用しているが、その判例が本件に適用される理由を示していない(さらに言うと、PTABはこの判例を引用するのは的外れである、と結論している)。
　以上の理由から、PTABは審査官による特許請求項1～10、13～15、17～26および 29～31の書面による説明の拒絶を破棄した。

【3】特許請求項1の説明　
　特許請求項1は、｢線形代数方程式Ax＝bを、変分アルゴリズムを使って量子コンピューターで解く｣発明について、記述している。ここで、Aは行列で、x及びbはベクトルである。一般に、Aはユニタリ行列(演算子)でもなく、射影行列(演算子)でもない。本決定の結論に影響を与えないので(表記を簡単にするため)、Aをユニタリ行列と仮定しよう。また、量子コンピューターによる計算が前提なので、純粋状態で考えてよい。
　古典系でAx＝b表現した方程式を、量子系ではǍ|x⟩＝|b⟩と表す。ただし、量子系は確率の世界なので、正規化する必要があり、Ǎ|x⟩は、Ǎ|x⟩/正規化定数となる。正規化定数＝√⟨x|Ǎ^†Ǎ|x⟩である^🐾5。このǍ|x⟩/正規化定数を|Φ⟩と置くと、量子系の線形代数方程式は、|Φ⟩＝|b⟩となる。そして、最適化問題におけるコスト関数Cは、C＝1－｜⟨b|Φ⟩｜²とすることができる(もちろん一意ではない。また、本特許では、異なる関数形である)。
　量子状態の準備とは、|x⟩と|b⟩を量子回路上で表現することである。初期状態|0⟩に、適当なパラメータ付きユニタリ回路V(𝜃)を作用させて、準備する。つまり、|x⟩＝V_x(𝜃)|0⟩、|b⟩＝V_b(φ)|0⟩のようにする。本特許では、|x⟩＝V_x(𝜃)|0⟩|x⟩＝|ψ(𝜃)⟩とおいている。|ψ(𝜃)⟩と|b⟩を準備すると、コスト関数が準備できる。故に最適化問題経由で、線形方程式の求解ができる、という流れである。この、|ψ(𝜃)⟩の準備が、争点となっている。
🐾5　Ǎが射影行列(演算子)ではないので、√⟨x|Ǎ^†Ǎ|x⟩となっている。言わずもがな、†は、エルミート共役を意味する。射影行列であれば、少しスッキリして、√⟨x|Ǎ|x⟩で済む。

【4】考察
(0)　2つの争点：❶量子状態の準備が、特許不適格なアイデアか否か。❷特許明細書におけるコスト関数の記載に不備があるか否か、に対するPTABの審査結果は、｢❶→ 特許不適格ではない、❷→不備なし｣である。 ❶の審査結果には不同意。 ❷の審査結果には同意。

(1)　ここで、状態準備について整理する。量子シミュレーションであれ、量子機械学習であれ、古典データを使って量子計算を行うのであれば、状態準備は重要かつ鬼門である。古典的な入力データを量子状態に符号化する｢状態準備｣を実行する量子回路の深さは、最悪の場合、指数関数的に増加する可能性がある。つまり、指数関数的な時間を要する可能性がある^🐾6。従って、量子計算そのものが指数関数的に速くても、相殺される。故に、計算複雑性の意味で量子優位性を求めている場合には、量子計算を選択する意味がなくなる。ただし、特定クラスに属する古典データは、多項式的深さの(つまり浅い)量子回路で、状態準備が可能であることが分かっている。すなわち、多項式時間で状態準備が可能である。
　例えば｢物性シミュレーションで、最初に量子優位性が実現する｣と述べる論文(24年4月29日@npj quantum information)[*N-3]は、特定の物性モデルでは、状態準備が多項式時間で行えることを、数値的に確認している。詳細は、こちらを参照。
　また、特定の確率分布(レヴィ分布、対数正規分布及びガンマ分布)が、浅い量子回路で符号化できる(多項式時間で状態準備可能である)ことも示されている。詳細は、こちらを参照。
🐾6　なお、状態準備は量子計算の入口に相当するが、出口である読み出し(測定)においても、同じことが起きる。量子データを古典データに変換するために、最悪の場合、指数関数的な時間を要する。

(2)　(1)で整理した通り、状態準備に指数関数的な時間を要するのであれば、古典計算の代わりに量子計算は使うという選択肢はない。従って、多項式時間で状態準備できる｢発明｣でなければ、特許の有効性はないと思われる。その理由を日本の特許･実用新案審査基準で言えば、｢発明の課題を解決するための手段は示されているものの、その手段によっては、課題を解決することが明らかに不可能なもの｣(第Ⅲ部第1章2.1.6)に該当すると思われるからである。本決定に即して言い換えれば、古典コンピューターで行えないことを量子コンピューターで行う(古典アルゴリズムよりも速く計算する)という試みが破綻するからである。
　ただし、全ての場合に対して、多項式時間で状態準備することはできない。このため、(1)でも示したように、特許の対象は特定の場合に絞る必要がある。実際、本特許においても、 多項式時間で状態準備できる場合に絞っている。物性シミュレーションや量子化学計算を具体的にイメージし、それらの”近似計算”で現れる線形代数方程式を、変分量子アルゴリズムで解く想定だと思われる。ただし、 多項式時間で量子状態を準備する量子アルゴリズムを具体的には提示していない(はず)。

(3)　具体的に提示とは、例えば、次のようなケースである。Zapataは、それなりに多くの特許を出願し、また特許付与もされている。Zapata(のYudong Cao)が、2019年10月4日に特許申請し、2021年11月9日に特許付与されたHybrid quantum-classical computer for variational coupled cluster method(特許番号11169801)は、量子化学計算で用いられる結合クラスター法の亜種である、変分結合クラスター法に関する特許である。この特許では、強相関電子系を対象として、｢結合クラスター演算子の”特殊な構造”を利用して、それを1量子ビットのパウリ行列のテンソル積の線形結合として記述し、多項式時間で量子状態を準備する量子アルゴリズムを提供｣している。
　状態準備とは、具体的な量子回路の設計を意味している。より具体的には、1量子ビットゲート(回転ゲート)の組み合わせを設計することを意味している。変数の数が少ない場合は、自明に行えるが、変数の数が増えた場合に、層の数を多項式的な増加に抑えることは難しい。しかし、だからと言ってすぐさま発明の要件を、十分に満たすとは言えないだろう。過去の判例(Mayo Collaborative Servs. v. Prometheus Labs., Inc., 2012)で、｢単に汎用的なコンピュータ実装を要求するだけでは、その抽象的なアイデアを特許適格な発明に変換することはできない｣と判示されているのだから、上記特許(特許番号11169801)にように、具体的に量子アルゴリズムを提示しなければ、特許有効性は認められないように思う。

(4)　本決定に従って特許が認められたら、他企業等に、どのような影響が及ぶのだろうか。他企業等とは、例えば、イスラエルのClassiqである。もっとも、米国には特許付与後に異議を申し立てる制度がある^🐾7。米国では、2011年に成立したAIA(☞🐾2参照)によって、新たに規定された。当事者系レビュー(IPR：Inter Partes Review)と付与後レビュー(PGR：Post Grant Review)が存在する[*N-4]。申立てが行われると予想する。
🐾7　やや古い資料(☞下記出典)によると米国、ドイツ、欧州(欧州特許庁)に、異議申立制度がある。日本では、2014年の特許法改正によって異議申立制度が導入された(施行は2015年4月1日)。
出典：淺見節子、公正取引委員会競争政策研究センター講演資料｜特許付与後レビュー制度の導入について―無効な特許による競争の阻害の是正―、平成26(2014)年3月7日、https://www.jftc.go.jp/cprc/katsudo/bbl_files/169th-bbl.pdf

❚為参考❚[*N-5],[*N-6],[*N-7]
　政権交代に伴って、USPTOの(バイデン前大統領に任命された)Kathi Vidal長官は、2024年12月での退任を発表。後任候補に、デリック･ブレント副長官の名も上がっていたが、トランプ大統領は、ジョン・スクワイアーズ氏を次期長官として正式に指名した(25年3月10日)→25年9月22日就任。商務省知的財産担当次官を兼任。
　スクワイアーズ氏は、金融界における著名な知財担当弁護士であり、｢フィンテック、ブロックチェーン及びAI分野｣が専門。学生時代は理系(専門は、化学)。2000～2009年には、ゴールドマン･サックスにおいて知財部門を率いていた。デリック･ブレント氏も、学生時代は理系(専門は機械工学)。

【尾註】
*A-1　https://www.riken.jp/pr/news/2021/20211215_3/index.html
*A-2　https://hbr.org/2013/10/special-forces-innovation-how-darpa-attacks-problems
*A-3　https://wellcomeleap.org　
*A-4　https://wellcomeleap.org/q4bio/　
*A-5　PASQALは、仏Qubit Pharmaceutical(及びユニタリーファンド)と協業するようである。Qubit Pharmaceuticalは、現状スパコン上で稼働している創薬プラットフォームをNISQ、FTQCへとデプロイしていく意向。
*A-6　Tanvi P. Gujarati et al.、Quantum computation of reactions on surfaces using local embedding、https://www.nature.com/articles/s41534-023-00753-1.epdf?sharing_token=BaGL3KAtVP7f2AUqc5YUt9RgN0jAjWel9jnR3ZoTv0MzxNIuj-XaUgEeODtnNwbH8eQ8KiuHwe9jF0E92UsLMTmq3czaRrlP5MEW3FfMjg-TfprHsLMhZJsHXrkqEMBoG5S27SIVjiPPJyV5C2hJ_qpZHVMSR8IqQvEgctlqy9s%3D
*A-7　npj Quantum Informationで公開されたのが23年9月12日。arXivには22年4月7日(第2版、第1版は3月14日)に公開されている。
*A-8　Kalpak Ghosh et al.、Deep Neural Network Assisted Quantum Chemistry Calculations on Quantum Computers、https://pubs.acs.org/doi/10.1021/acsomega.3c07364
*A-9　https://dojo.qulacs.org/ja/latest/notebooks/6.1_openfermion_basics.html
*A-10　https://arxiv.org/ftp/arxiv/papers/2304/2304.04516.pdf
*A-11　https://docs.quantum.ibm.com/run/configure-error-mitigation
*A-12　Supporting Information for Deep Neural Network Assisted Quantum Chemistry Calculations on Quantum Computers、https://pubs.acs.org/doi/suppl/10.1021/acsomega.3c07364/suppl_file/ao3c07364_si_001.pdf
*A-13　理研、東京理科大、東大。
*A-14　Sahel Ashhab et al.、Quantum circuit synthesis via a random combinatorial search、https://arxiv.org/pdf/2311.17298
*A-15　Jun Zhang et al.、Minimum construction of two-qubit quantum operations、https://arxiv.org/pdf/quant-ph/0312193
*A-16　人工知能(AI)研究に冬の時代があったことは、広く知られている。AIゴッドファーザーの一人、ヤン･ルカンは、NEC北米研究所に在籍していたが、NEC本社がAIに興味を失った(事業リストラで、それどころではなかった?)ため、NECを離れることとなった^🛡1。NECに先見の明があれば、日本のAI風景は全く違っていたかもしれない。
🛡1　ヤン・ルカン、ディープラーニング 学習する機械 ヤン・ルカン、人工知能を語る、講談社サイエンティフィック、2021
*A-17　NTTコンピュータ&データサイエンス研究所、大阪大学。
*A-18　Nobuyuki Yoshioka et al.、Hunting for quantum-classical crossover in condensed matter problems、https://www.nature.com/articles/s41534-024-00839-4
*A-19　Johannes Aspman et al.、Robust Quantum Gate Complexity: Foundations、https://arxiv.org/pdf/2404.15828
*A-20　柴田心太郎、ゴミラインをもつ量子桁上げ伝播加算器回路の深さに関する最適化、https://www.st.nanzan-u.ac.jp/info/ma-thesis/2019/yokoyama/pdf/m18se012.pdf
*A-21　田崎晴明、Hubbard 模型の物理と数理、https://www.gakushuin.ac.jp/~881791/pdf/KBHubbard.pdf
*A-22　Craig Gidney et al.、How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits、https://arxiv.org/pdf/1905.09749。査読済版は、https://quantum-journal.org/papers/q-2021-04-15-433/pdf/
　ちなみに、日本総合研究所の資料^🛡2には、200万と書かれている(つまり、誤植。ただし誤植自体、大きな問題ではない)。→アップデート資料^🛡3では、訂正されている。
🛡2　株式会社日本総合研究所先端技術ラボ、量子コンピュータの概説と動向～量子コンピューティング時代を見据えて～、2020年7月14日、https://www.jri.co.jp/MediaLibrary/file/column/opinion/pdf/11942.pdf
🛡3　株式会社日本総合研究所先端技術ラボ、量子コンピュータの動向と展望、2024年11月7日(ver.1.1、ver1.0は10月29日)、https://www.jri.co.jp/MediaLibrary/file/advanced/advanced-technology/pdf/15330.pdf
*A-23　23年1月、富士通の発表(https://pr.fujitsu.com/jp/news/2023/01/23.html)。ちなみに、21年9月に発表された別の論文(https://arxiv.org/pdf/2103.06159)では、13,436量子ビットで177日だったので、少し進歩している。
*A-24　https://www.zapata-ai.jp/post/quantum-cryptography-jp
*A-25　Alexander M. Dalzell et al.、Quantum algorithms: A survey of applications and end-to-end complexities、https://arxiv.org/pdf/2310.03011
*A-26　Yasunori Lee & Keita Kanno、Modal analysis on quantum computers via qubitization、https://arxiv.org/pdf/2307.07478
　日本語かつ噛み砕いた資料だと、以下：菅野恵太、量子位相推定アルゴリズムを用いた量子コンピュータによる固有振動数解析、https://unit.aist.go.jp/g-quat/ja/events/img/CAE_20240509-10/20240510_10_Kanno.pdf
*A-27　カタロニア･ナノサイエンスおよびナノテクノロジー研究所(ICN2)、ドノスティア国際物理センター財団、バスク科学財団(Ikerbasque)
*A-28　Andrei Tomut et al.、CompactifAI: Extreme Compression of Large Language Models using Quantum-Inspired Tensor Networks、https://arxiv.org/pdf/2401.14109
*A-29　https://multiversecomputing.com/resources/eu-funded-ai-boost-project-selects-multiverse-computing-to-develop-and-train-large-scale-ai
*A-30　Dan Hendrycks et al.、MEASURING MASSIVE MULTITASK LANGUAGE UNDERSTANDING、https://arxiv.org/pdf/2009.03300
*A-31　尹 子旗他、プロンプトの丁寧さと大規模言語モデルの性能の関係検証、言語処理学会 第30回年次大会 発表論文集(2024年3月)、https://www.anlp.jp/proceedings/annual_meeting/2024/pdf_dir/A7-5.pdf
*A-32　Rowan Zellers et al.、HellaSwag: Can a Machine Really Finish Your Sentence?、https://arxiv.org/pdf/1905.07830
*A-33　植松 拓也他、日本語 Natural Questions と BoolQ の構築、https://www.anlp.jp/proceedings/annual_meeting/2024/pdf_dir/C3-3.pdf
*A-34　Christopher Clark et al.、BoolQ: Exploring the Surprising Difficulty of Natural Yes/No Questions、https://arxiv.org/pdf/1905.10044
*A-35　鈴木 正敏、JAQKET: クイズを題材にした日本語 QA データセットの構築、https://www.anlp.jp/proceedings/annual_meeting/2020/pdf_dir/P2-24.pdf
*A-36　Mandar Joshi et al.、TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension、https://arxiv.org/pdf/1705.03551
*A-37　Karl Cobbe et al.、Training Verifiers to Solve Math Word Problems、https://arxiv.org/pdf/2110.14168
*A-38　V. Abronin et al.、TQCompressor: improving tensor decomposition methods in neural networks via permutations、https://arxiv.org/pdf/2401.16367
*A-39　Pablo Arnault et al.、A typology of quantum algorithms、https://arxiv.org/pdf/2407.05178
*A-40　https://www.quera.com/press-releases/all-three-projects-powered-by-quera-computing-contributions-move-to-phase-two-of-wellcome-leaps-quantum-for-bio-challenge-focused-on-healthcare-and-biology-applications
*A-41　Lei Yu et al.、GQWformer: A Quantum-based Transformer for Graph Representation Learning、https://arxiv.org/pdf/2412.02285v1
*A-42　Yaswitha Gujju et al.、QUANTUM MACHINE LEARNING ON NEAR-TERM QUANTUM DEVICES: CURRENT STATE OF SUPERVISED AND UNSUPERVISED TECHNIQUES FOR REAL-WORLD APPLICATIONS、https://arxiv.org/pdf/2307.00908
*A-43　御手洗光祐、量子コンピュータの機械学習応用の可能性、https://www.jst.go.jp/moonshot/sympo/20241001/pdf/09_mitarai.pdf
　上記資料は、24年10月1日に行われた、国立研究開発法人科学技術振興機構 ムーンショット目標6　ミニシンポジウム2024における資料である。ムーンショット目標6は、｢2050年までに、経済・産業・安全保障を飛躍的に発展させる誤り耐性型汎用量子コンピュータを実現｣である。
*A-44　M. Cerezo et al.、Does provable absence of barren plateaus imply classical simulability? Or, why we need to rethink variational quantum computing、https://arxiv.org/pdf/2312.09121.pdf
*A-45　Nico Meyer et al.、A Survey on Quantum Reinforcement Learning、https://arxiv.org/pdf/2211.03464
*A-46　Huang Bojun、Steady State Analysis of Episodic Reinforcement Learning、https://proceedings.neurips.cc/paper/2020/file/69bfa2aa2b7b139ff581a806abf0a886-Paper.pdf
*A-47　 Luca Lusnig et al.、Hybrid Quantum Image Classification and Federated Learning for Hepatic Steatosis Diagnosis、https://www.mdpi.com/2075-4418/14/5/558
*A-48　Zeheng Wang et al.、Self-Adaptive Quantum Kernel Principal Component Analysis for Compact Readout of Chemiresistive Sensor Arrays、https://advanced.onlinelibrary.wiley.com/doi/10.1002/advs.202411573
*A-49　Aleksandr Berezutskii et al.、Tensor networks for quantum computing、https://arxiv.org/pdf/2503.08626
　査読済版(25年7月30日)は、https://www.nature.com/articles/s42254-025-00853-1
*A-50　大久保毅、テンソルネットワークと量子計算、https://masazumihonda.github.io/QCschool2023.github.io/slides/Okubo.pdf
*A-51　https://www.quera.com/press-releases/two-projects-powered-by-quera-computing-contributions-move-to-phase-three-of-wellcome-leaps-quantum-for-bio-challenge-focused-on-healthcare-and-biology-applications
*A-52　https://www.quemix.com/post/press-honda-quantum-readout-newtech
*A-53　Hirofumi Nishi et al.、Quantum State Readout via Overlap-Based Feature Extraction、https://arxiv.org/pdf/2505.08613
*A-54　Sang Hyub Kim et al.、Quantum Large Language Model Fine-Tuning、https://arxiv.org/pdf/2504.08732
*A-55　Taiki Kawamuro et al.、Quantum Machine Learning for Identifying Transient Events in X-Ray Light Curves、https://iopscience.iop.org/article/10.3847/1538-4357/adda43/pdf
*A-56　竹中透、「人間型ロボット『アシモ』開発の裏話」、本田財団レポート No.99、https://www.hondafoundation.jp/data_files/view/300
*A-57　Takuya Otani et al.、Quantum computation for robot posture optimization、https://www.nature.com/articles/s41598-025-12109-0.pdf
*A-58　Qi Zhao et al.、Entanglement accelerates quantum simulation、https://arxiv.org/pdf/2406.02379
*A-59　Daniel Beaulieu et al.、Robust Quantum Reservoir Learning for Molecular Property Prediction、https://pubs.acs.org/doi/full/10.1021/acs.jcim.5c00958
*A-60　https://arxiv.org/pdf/2412.06758
*A-61　Milan Kornjaˇca et al.、Large-scale quantum reservoir learning with an analog quantum computer、https://arxiv.org/pdf/2407.02553
*A-62　欠番
*A-63　O. Lanes et al.、A framework for quantum advantage、https://arxiv.org/pdf/2506.20658
*A-64　Ryan Mandelbaum et al.、The dawn of quantum advantage、https://www.ibm.com/quantum/blog/quantum-advantage-era
*A-65　Hsin-Yuan Huang et al.、The vast world of quantum advantage、https://arxiv.org/pdf/2508.05720
*A-66　Nobuyuki Yoshioka et al.、Krylov diagonalization of large many-body Hamiltonians on a quantum processor、https://www.nature.com/articles/s41467-025-59716-z.pdf
*A-67　Urmila Mahadev et al.、Classical Verification of Quantum Computations、https://arxiv.org/pdf/1804.01082
*A-68　Sisi Zhou et al.、Achieving the Heisenberg limit in quantum metrology using quantum error correction、https://www.nature.com/articles/s41467-017-02510-3.pdf
*A-69　Andrew D. King et al.、Beyond-classical computation in quantum simulation、https://www.science.org/doi/10.1126/science.ado6285
*A-70　Humberto Munoz-Bauza1 ＆ Daniel Lidar、Scaling Advantage in Approximate Optimization with Quantum Annealing、https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.134.160601
*A-71　Hua-Liang Liu et al.、Robust quantum computational advantage with programmable 3050-photon Gaussian boson sampling、https://arxiv.org/pdf/2508.09092
*A-72　Élie Gouzien et al.、Performance Analysis of a Repetition Cat Code Architecture: Computing 256-bit Elliptic Curve Logarithm in 9 Hours with 126133 Cat Qubits、https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.131.040602
*A-73　Diego Ruiz et al.、LDPC-cat codes for low-overhead quantum computing in 2D、https://www.nature.com/articles/s41467-025-56298-8.pdf
*A-74　Craig Gidney、How to factor 2048 bit RSA integers with less than a million noisy qubits、https://arxiv.org/pdf/2505.15917
*A-75　Jens Eisert＆John Preskill、Mind the gaps: The fraught road to quantum advantage、https://arxiv.org/pdf/2510.19928
*A-76　https://blog.haiqu.ai/quantum-embeddings-for-anomaly-detection-a-new-lens-on-data-representation-2/
・・・
*A-96　https://www.holdings.toppan.com/ja/news/2025/09/newsrelease250908_2.html
*A-97　Takao Tomono & Kazuya Tsujimura、Quantum Kernel Anomaly Detection Using AR-Derived Features from Non-Contact Acoustic Monitoring for Smart Manufacturing、https://arxiv.org/pdf/2510.05594
・・・
*A-99　Taichi Matsubara et al.、QTFPred: robust high-performance quantum machine learning modeling that predicts main and cooperative transcription factor bindings with base resolution、https://academic.oup.com/bib/article/26/6/bbaf604/8343189
・・・
*A-108　Rajiv Kailasanathan et al.、Quantum enhanced ensemble GANs for anomaly detection in continuous biomanufacturing、https://arxiv.org/pdf/2508.21438
*A-109　瀧田雄太、識別器は本当に目標分布を学習しているのか？GANの解析とSlicing Adversarial Networkによる改善、https://www.jstage.jst.go.jp/article/jnns/31/4/31_187/_pdf/-char/ja
*A-110　Photonic Inc.、SHYPS to Shor's　A Call for Distributed QRE(WHITE PAPER)、https://photonic.com/wp-content/uploads/2025/12/SHYPS-to-Shors-Whitepaper.pdf

*N-1　https://developer.uspto.gov/ptab-web/#/search/documents?proceedingNumber=2024002159
注)　Document Title欄下にあるDecisionをクリックすると、pdfファイルがダウンロードされる。
*N-2　https://patents.google.com/patent/US20200104740A1/en?inventor=Yudong+Cao&assignee=Zapata&oq=Zapata%E3%80%80Yudong+Cao
*N-3　Nobuyuki Yoshioka et al.、Hunting for quantum-classical crossover in condensed matter problems、https://www.nature.com/articles/s41534-024-00839-4　
*N-4　守安智･小川亮･齊藤彬、AIA後の米国における特許付与後の手続き、tokugikon 2018.1.25 no.288、pp.32-41、http://www.tokugikon.jp/gikonshi/288/288tokusyu4.pdf
*N-5　https://openlegalcommunity.com/uspto-director-vidal-announces-resignation-impact-on-ip-practice-and-future-trends/
*N-6　https://www.itohpat.co.jp/ip/2520/
*N-7　http://www.tatsuoyabe.aki.gs/2025-02-25_Lutinick_and_PTO_New_Director.html

お問い合わせ