Ⅰ　概要
　　Ⅱ　金融実務でMCMCが使われている場面
　　Ⅲ　乱数発生アルゴリズム
　　Ⅳ　モデル選択基準の指標、収束性判断の指標、事前確率分布について
　　Ⅴ　感想と情報

【1】MCMCの始まり
　MCMCは、主にロスアラモス国立研究所で活動した、米国の物理学者ニコラス･コンスタンチン･メトロポリス他が、液体－固体の相転移に関する統計力学的研究のため1953年に開発したとされている(論文は他4名との共著)。ちなみに同研究は、ロスアラモス研究所が開発した(軍事研究が主要ターゲットであった)　MANIAC[注1]というコンピュータを使って実施された。

【2】統計モデルとパラメータ推定法－MCMCはパラメータ推定法である！
　MCMCが、統計学の分野(パラメータ推計)にも応用されたのは実質的に1990年代である。統計モデルとパラメータ推定法について少し整理する。
　(1)　最小二乗法と線形モデル　
　パラメータ推計と言えば、回帰分析(線形の統計モデル)における最小二乗法が有名である。線形モデルは、目的変数＝説明変数の線形和＋誤差項と仮定した統計モデルである。この説明変数の線形和を、線形予測子と呼ぶ。念の為、線形予測子を書き下すと以下のようになる。
　　　線形予測子＝β₀＋β₁･x₁＋β₂･x₂＋β₃･x₁²＋･･･
　実は、線形予測子は、係数(上式ではβ)目線での線形和なので、説明変数のべき乗が含まれていても構わない。
　線形モデルの誤差項は、等分散正規分布に従うと仮定している。これはつまり「説明変数と目的変数とが等分散正規分布の関係にある」と仮定していることになるが、この後者の仮定から、線形モデルのみ、残差平方和を最小にする最小二乗法によってパラメータ(説明変数の係数)推定が可能となる。
　つまり理屈から言うと、パラメータ推定法としての最小二乗法は適用可能ケースが限定される。その一方で、線形モデル自体は極めてポピュラーであるため、最小二乗法もパラメータ推定法としてポピュラーとなっている。
　「説明変数と目的変数とが等分散正規分布の関係にない」場合は、最小二乗法は使えないので最尤法を用いる。もちろん、線形モデルでも最尤法は使用できる。線形モデルの誤差項が正規分布の場合、最尤法と最小二乗法の結果は一致する。
　実務では、線形モデルが適用できるかできないかに関わらず、以下のようなことが行われている：①まず最小二乗法で推計して、②パラメータ推定の信頼性(｢当てはまりの良さ｣や｢統計的有意性｣)が、(決定係数やｔ値で判断して)不足している場合は、③最尤法でのパラメータ推定との比較考量の上、④パラメータを決定する。

　(2)　最尤法と一般化線形モデル(GLM)　
　①一般論
　説明変数と目的変数との関係を、等分散正規分布以外の確率分布に拡張した統計モデルを一般化線形モデル(GLM)という。
　GLMで用いられる(等分散)正規分布以外の確率分布としては、ポワソン分布、二項分布あるいはガンマ分布などが代表的である。GLMは(実際はGLMのみならずGLMMも)、目的変数の期待値(平均値)を中心として、『目的変数の確率分布、線形予測子、リンク関数』という3要素で構成されている、と整理すると見通しが良くなる。
　目的変数の確率分布では、確率分布の母数に、目的変数の平均値が関係づけられる。別の言い方をすると確率変数の母数が平均値と簡単な関係式で結び付く確率分布でなければ、GLM(及びGLMM)では扱えない。その一方で、平均値はリンク関数で変換された値を通して、説明変数とパラメータの線形和である線形予測子と結び付く。
　このように、平均値を中心において、目的変数が説明変数と結び付いている。
　GLMでは、3つの要素を組み合わせることで、説明変数と目的変数との関係を、等分散正規分布以外の確率分布に拡張する。
　線形モデルでは、誤差項が(等分散)正規分布に従うため、目的変数の期待値＝線形予測子というシンプルな関係が成立していた。線形でない非線形モデルにおいて、｢工夫なし｣では、このシンプルな関係は成立しない。目的変数の期待値を変換する、という工夫で、シンプルな関係を復元するのがGLMである。目的変数の期待値を変換する関数が、リンク関数である。目的変数の期待値をリンク関数で変換したものが線形予測子である。
　線形モデルは、リンク関数が恒等関数である一般化線形モデルと捉えることができる。
　代表的なGLMには、プロビットモデルやロジットモデルがある。どちらも確率分布(説明変数と目的変数との関係。別の表現をすれば、誤差項)は二項分布であるが、リンク関数が異なる。プロビットモデルはプロビット関数。ロジットモデルは、リンク関数がロジット関数である(ロジット関数の逆関数が(標準)ロジスティック関数)。
　GLMにおけるパラメータ推定は、最尤法で行われる。最尤法では、まず尤度関数と呼ばれる関数を作り、尤度関数が最大となるパラメータを探索することで、パラメータ推定を行う。一般には計算の容易さから、尤度関数の対数をとった、対数尤度関数の和が最大になるような計算を行う。尤度関数が複雑で最大化問題を解くことが難しい場合等は、数値計算を行う。

　②ベイズ化GLM
　普通のGLMでは、線形予測子に現れる説明変数の係数(パラメータ)を確定値として扱う。パラメータが何らかの確率分布に従うと考え、ベイズの定理でパラメータ推定を行うとベイズ化GLMとなる。ただし、個々の目的変数全体に対して、ばらつきをもたらす確率分布を与えるわけではない。従って、統計モデルとしての進化はない。ベイズ化GLMとプレーンなGLMの違いは、パラメータの推定法の方法論が異なるというだけである。
　ベイズモデルでは、ベイズの定理：事後分布∝尤度×事前分布を利用する。最尤法を用いて、尤度を最大化するパラメータの事後分布を求める。

　③階層ベイズ化GLM
　確率分布の母数が確率分布に従うモデルを一般には、階層モデルと呼ぶ。このため、事前分布の母数が、確率分布に従うと設定する統計モデルは、階層ベイズモデルと呼ばれる。
　事前分布を階層化したGLMは、階層化ベイズGLMとなる。ただし、階層化ベイズGLM は意味がない。個々の目的変数に対してばらつきをもたらす確率分布を与えることは、多数のパラメータを新たに導入することを意味する。その多数のパラメータをコントロールするために、超事前分布を導入するのである。GLMでは｢個々の目的変数全体に対して、ばらつきをもたらす確率分布を与えるわけではない｣ので、階層ベイズモデルという形態は意味がない。

　(3)　一般化線形混合モデル(GLMM)とMCMC　
　①一般論
　モデルは(自然界などの)複雑さを取捨して本質を抽出するための道具であるが、「目的変数を少数の説明変数だけで表現する」という枠組みに限界を感じることもあるだろう。
　その閉塞状況を打破する方法として、線形予測子に確率変数を導入するという方法がある。下記[A]～[C]のように確率変数を導入した一般化線形モデルを一般化線形混合モデル(GLMM)と呼ぶ。

[A]　例えば、目的変数が生体内反応である場合。生体内反応はどう考えても複雑であるから、少数の説明変数で説明できないと考える方が自然であろう。生体内反応には負けるかもしれないが、株価だって複雑な要因で決定されているに違いない。
　そういった場合、"少数の説明変数"以外の説明変数を考慮してやればよいが、それを確率変数という形で与えるというアイデアがありうる。観測しなかったあるいは観測できない説明変数を、確率変数として｢ドバっと｣取り込むイメージである。このケースは、ランダム切片モデルとも呼ばれる。
　数式的に表現すると、添え字iで区分される目的変数に対して、添え字iで区分される確率変数が線形予測子に加わる。つまり個々の目的変数に対してバラつきをもたらす確率分布を導入する。

[B]　また説明変数が、｢業務知識｣から判断して大括り過ぎるというケースがあるだろう。あるいは、目的変数と説明変数との間の関係が一定ではなく、場合分けが必要なケースがあるだろう。それらの場合は、説明変数も小分け(場合分け)してやれば良い、ということになる。この場合は、線形予測子における説明変数の係数が小分け(場合分け)されることになる。このケースは、ランダム係数モデルとも呼ばれる。
　数式的に表現すると、｢GLMでは添え字iで区分される目的変数に対して、係数は添え字iで区分されていない」が、｢GLMMでは、係数が添え字iで区分されている｣。つまり個々の目的変数に対してバラつきをもたらす確率分布を導入する。

[C] 　上記2つは、数式的なアプローチなのでピンとこないかも知れない。感覚的に理解しやすい、視覚的なアプローチでGLMMを表現してみよう。GLMは目的変数の確率分布(目的変数のばらつき)をよく知られた1種類の確率分布と決めつけている。代表的には、二項分布、ポアソン分布あるいはガンマ分布などである。
　GLMMでは、甲)新たに導入される個々の目的変数に対して大きなバラつきをもたらす確率分布が与えられる。｢大きなバラつき＝過分散｣としたのは｢小さなバラつき｣であれば無視できるからである。大きなバラつきを与えた結果として、更に、目的変数の期待値まで変動させることができる。その場合は、乙)目的変数の期待値の変動を表現する確率分布と甲の確率分布とが合成された｢新しい確率分布｣を目的変数が本当に従う確率分布と改めて見做す。そうすることで、現象あるいは観測事実に対する統計モデルの近似精度が、より高まることが期待される。
　まとめると、確率分布を合成するという方法を採用することで、統計モデルの精度を向上させることがGLMMの本質である。

　②ベイズ化と階層化
　ベイズ公式でパラメータ推定を行うとGLMMはベイズ化GLMMであるが、階層化しないということは通常は考えられない。個々の目的変数に対してバラつきをもたらす確率分布を与えることに伴って、新たに導入される多数のパラメータをコントロールするために、超事前分布を導入するからである。

　③MCMCの必要性
　GLMMでも最尤推定は可能である。GLMM の一般的な尤度計算方法として、EMアルゴリズム、ガウス‐エルミート求積法、ラプラス近似法が知られている。EMアルゴリズムは、【4】の(3)で簡単に触れる。
　しかしパラメータの数が多くなると最尤推定の結果は信頼性を失うとされ、他の推定法が要求される。通常の最尤推定法では、パラメータが 5 個以上の推定は実際上不可能であるとされる。そこでMCMCが登場する。
　専門家によると階層構造を持っているモデル(階層ベイズモデル)には最尤法は適用推奨できない。

【3】最尤法とMCMCの違い及びMCMCの長所と短所
　最尤法とMCMCは、根本的な発想が異なる。最尤法は最適化手法であり、尤度を最大にするパラメータを決定することが目的である。一方MCMCは、適当な初期値から少しずつ移動していくことで、尤度関数全体を探ることでパラメータの確率分布を推定することが目的である。
　MCMC 法には、（1）さまざまな確率分布に適用可能、（2）多変量の場合にも適用可能、（3）尤度関数が多峰形であっても大域的ピークを探索可能、（4）計算量の省力化が行える[注2] 、等の長所がある。一方で、時間がかかるといった短所がある。

【4】数学的な整理と追記
　(1)　順序選択モデル　
　目的変数が質的変数(あるいはダミー変数)である統計モデルは、順序選択モデルと呼ばれる。質的変数(あるいはダミー変数)とは、宝くじが当たった･当たらない、炭治郎･伊之助･善逸のうち誰が一番が好きかに対する答え、といった変数を言う。順序プロビットモデルや順序ロジットモデルが広く知られている。目的変数が質的変数であるプロビットモデルを、順序プロビットモデルと呼ぶ。
　順序選択モデルは、金融ではポピュラーである。デフォルト推定、格付け推移、信用リスク管理といったケースで現れる。なお統計モデルとしては、順序プロビットモデル(あるいは順序ロジットモデル)が使われる。
　順序プロビットモデルや順序ロジットモデルは目的変数が順序付けられていたが、目的変数が順序付けられていない場合は、多項プロビットモデルや多項ロジットモデルと呼ばれる。順序付けられているとは、宝くじが当たった、当たらなかったのケース。順序付けられていないとは、炭治郎･伊之助･善逸のうち誰が一番が好きかのケースである。
　ただし、前述したように金融分野で、多項プロビットモデルや多項ロジットモデルに遭遇することは少ないと思われる。

　(2)　マルコフ連鎖の驚くべき性質　
　MCMCは、未知のパラメータが従う未知の確率分布を同時に推計できる、という驚くべき性質を有している。これは、マルコフ連鎖の性質に由来している。
　ある条件を課すことで、マルコフ連鎖は定常分布を持つ。定常分布とは、「大きな回数」繰り返すとマルコフ連鎖がその分布からの乱数発生となる確率分布である。具体的な「大きな回数」を決定する方法はない。もちろん、(統計)数学的な手法は存在するが、人の判断が必要となる。作業をある程度多数(例えば10万回とか)繰り返すことで、マルコフ連鎖は定常分布に収束し、定常分布が、パラメータが従う(同時)確率分布となる。一般的には(ベイズ統計の文言として)事後確率と表現される。
　定常分布に達したかは、別途収束判断が必要であるが、定常分布に達した後は、マルコフ連鎖が｢適当な｣乱数列を生成することになる。｢適当な｣乱数列とは、観測データが観測されたという条件下でパラメータが従う確率分布(ただし、複数のパラメータの同時確率分布)に従った乱数という意味である。
　ある条件とは「つり合い条件」と「エルゴード性」である。つり合い条件と詳細つり合い条件は、異なるので注意。つり合い条件を満たすマルコフ連鎖の構成は難しいため、代わりにより強い条件である「詳細つり合い条件」を課したマルコフ連鎖を構成することが行われてきた。
　「詳細つり合い条件」を課したマルコフ連鎖の弱点は、時間がかかることである。現在は、「詳細つり合い条件」なしのマルコフ連鎖も構成されている(Ⅲ(5)①を参照)。

　不完全データから最尤推定値を求める方法と紹介されるEMアルゴリズムを理解するには、不完全データとは何を指しているのか？を理解することが欠かせない。
　不完全データとは必ずしも、外れ値や欠損値あるいはエラーを意味していない。実際に観測されたデータを不完全データと見做すことで、EMアルゴリズムは汎用的(かつ強力な)な最尤推定法となる。完全なデータは、観測できない変数(潜在変数)を追加して仮想的に導入することができる。この｢観測できない変数(＝非観測データ)｣の導入というワードから、直ちにGLMMとの親和性が思い浮かぶであろう。
　EMアルゴリズムは、不完全データ＝観測データの最尤推定を直接実行することは至難であるものの、完全データの最尤推定が簡単であれば、それを間接利用して、観測データの最尤推定を実行する数値アルゴリズムである。EMアルゴリズムは、EステップとMステップを繰り返すが、その反復によって、局所的には最適解に収束することが証明されている。ただし、大域的に収束する保証はない。
　EMアルゴリズムはもう少し、詳しく説明すると
　　　①完全データに対する対数尤度関数について、
　　　②パラメータ推定値と観測データの条件付期待値をとり最大化することで、
　　　③パラメータ推定値を逐次更新して行き、
　　　④観測データに対するパラメータの最尤推定値を得る
方法である。さらに詳しく言うと
　1)　パラメータθの初期値θ0を設定する。
　2)　Eステップ(期待ステップ)：
　非観測データzについて、完全データXに対する対数尤度関数の条件付期待値Qを計算する。
　　　　　　　Q(θ｜θ^k)＝∫L(θ｜X)×f(z｜ｙ、θ) dz
　ここで
　　　　　　　θ^k：k段階目のパラメータ(k＝0,1,･･･)
　　　　　　　X：完全データ＝(ｙ、z)
　　　　　　　ｙ：観測データ
　　　　　　　L：完全データＸに対する対数尤度関数
　　　　　　　f：非観測データｚの条件付き確率分布
である。GLMMで導入する非観測データは確率変数であった。従って、そのときにfは与えられる。条件付き確率分布とは、観測データｙとパラメータθが与えられた下での確率分布という(普通の)意味である。
　積分計算は、総和に置き換えて計算する。もしくは乱数を使って(モンテカルロ法で)積分計算する。後者をMCEM(モンテカルロEMアルゴリズム)という。
　3)　Mステップ(最大化ステップ)：
　Q(θ｜θ^k)をθに関して最大化することでθ^k＋1を計算する。
　　　　　　　θ^k＋1＝argmax Q(θ｜θ^k)
　ここで
　　　　　　　argmax：最大点作用素
である。
　4)　EステップとMステップを収束するまで繰り返す。対数尤度関数Lの増加が、ある閾値より小さくなった時点で、収束したと判定する。

↑目次に戻る

【1】俯瞰
　金融実務では、以下の場面でMCMCが使用されている。
◆デリバティブの評価
　ブラックショールズ･モデルあるいはブラック･モデルはデリバティブの価格変化を表現する近似モデルであるから、どこかに歪みが生じたとしても不思議ではない。両モデルにおいては、ボラティリティが一手にその歪みを担っている。具体的には曲がっている。その曲がったボラティリティ－2次元だと、ボラティリティ･スマイル、3次元だとボラティリティ･サーフェイス－を可能な限り正確に表現できれば、デリバティブの価格付けの精度が向上する。
　そのような動機付けで、ボラティリティを正確に表現するモデル研究が行われ、その代表例として、確率的ボラティリティ(SV)モデルがある。SVモデルのパラメータ推定にMCMCが使われている。

◆株式収益率や外国為替相場の分析
　確率的ボラティリティ(SV)モデルはデリバティブの値付け以外にも用いられる。
　例えば株価収益率のようなリスク資産価格収益率のボラティリティは、経験的な事実として確率的に変動していることが知られている。そのためSVモデルの適用が妥当であるが、多くの潜在変数がモデルに存在する。このために通常の最尤法では(多重積分の存在により)解析的な扱いが困難であった。MCMCによりパラメータ推定が実行可能になった。

◆オペレーショナルリスクのVaR
　オペレーショナルリスクの損失額(分布)は、オペレーショナルリスクの頻度(発生頻度分布)と規模(影響度分布)を掛け合わせて算出する。発生頻度分布はポアソン分布を採用しても良いだろう。しかし、影響度分布は一般的に、よく知られた確率分布では表現できないと判断せざるをえない。
　そのような場合は、影響度分布を、よく知られた確率分布の合成として表現すれば良い。これはGLMMの箇所で説明した通りの状況であり、GLMMがフィットする。GLMMにおけるパラメータ推定法はMCMCが唯一の選択肢ではないが、推定すべきパラメータが多いと最尤法は使えないので、MCMCは有力な選択肢となる。

◆信用リスク－事業性融資
　【3】を参照。
◆信用リスク－個人向け住宅ローン
　【4】を参照。

【2】順序選択モデルを使った格付け推定、デフォルト率推定モデル
　順序モデルでは、企業の信用力を説明するために、説明変数とパラメータの線形和を｢信用力スコア(潜在変数)｣として用意する。なお、説明変数には財務指標等が使用される。
　さらに企業を、格付けに分別するしきい値を定める。しきい値を定めると、2つのしきい値で挟まれる区間が作成される。各区間には、それぞれ定められた格付けが、適切に割り当てられる。ある企業の信用力スコアが、ある区間内に含まれば、その企業には当該区間に対応する格付けが付与される(しきい値メカニズム)。住宅ローンのような個人向け融資においても、格付けに類似するグループ(債務者区分、もしくは債務者区分をもう少し細かくしたグループ)を作って、そこに信用力スコアを当てはめれば事業性融資と同じ構図となる。
　統計モデル的には、誤差込みの信用力スコアを考える。そして誤差項(ノイズ)の従う確率分布を与えてやることで、ある企業が、ある格付けに割り当てられる確率が表される。
　ある格付けに分別された企業集団から、1年後にデフォルトした企業の数をカウントすれば、当該格付けの(件数ベースの)1年デフォルト率(PD)が算出される。従って、PDの推定は割算値の推定とはならない(LGDも回収額を推定対象とすれば、割算値の推定とはならない)。
　プレーンな格付け推定モデルにおける順序モデルでは、信用力スコアを
　　　信用力スコア＝パラメータ×説明変数＋ノイズ
と表現する。

【3】事業性融資におけるMCMC
(1)　格付けの推定モデル・概論
　法人への貸付＝事業性融資の信用リスク評価は通常、格付けをベースとしている。つまり貸付先の格付けに応じたデフォルト率をベースとしている。
　格付け会社は格付け決定ロジックを公表していないから、自行内で企業を格付けする場合は、格付けロジックを設定する必要がある。一般的には、貸付先の財務情報を説明変数とした、順序プロビットモデルという単純なモデルを使用することが多い。目的変数が質的変数で、確率分布としては二項分布に従うとする。そしてリンク関数がプロビット関数(標準正規分布の累積分布関数の逆関数)である統計モデルが、順序プロビットモデルである。
　シンプルな順序プロビットモデルは、説明変数に掛け合わされている係数(パラメータ)は、企業毎の特性まで表現しない。つまり、業種の違いを考慮しない(つまり、収益が比較的安定している公益企業と、業績のブレが大きい企業も同じとみなす)。また地域の違いも考慮しない(つまり、地方と東京の企業も同じと見なす)。
　また格付けした時点の経済が、好況か不況かといった違いも考慮しない。
　観測していない若しくは観測できない企業毎の特性を考慮するとモデルが複雑になるが、信用リスク管理体系は、市場で直接観測できないファクター(frailtyフレイルティ)の存在を仮定し、その存在を考慮するという枠組みに移っている。この枠組みでは、最尤法によるパラメータ推定は困難であり自然に、MCMCの出番となる。
　プレーンな順序プロビットモデルでは、信用力スコアを
　　　　信用力スコア_i＝パラメータ×説明変数_i＋ノイズ_i
と表現する。
　順序プロビットモデルに観測していない企業毎の特性を考慮する方法として、(a) 特性を定数項の形で取り入れる、(b)パラメータに特性を取り入れる、という方法が考えられる。企業毎の特性という新たな情報を追加すると、新たな情報を表現するために添え字が増える。その下付き添え字をｊとすると
　　　(a)：信用力スコア_i,j＝特性を考慮した定数項_j＋パラメータ×説明変数_i,j＋特性を考慮したノイズ_i,j
　　　(b)：信用力スコア_i,j＝特性を考慮したパラメータ_j×説明変数_i,j＋特性を考慮したノイズ_i,j
である。特性を考慮したノイズとは、例えば、地域が異なれば、異なるノイズを採用するという意味である。GLMMでは、特性が、何らかの確率分布に従っていると仮定していることがポイントである。つまり特性を考慮した定数項jと特性を考慮したパラメータjは確率分布として導入する。確率分布を階層事前分布として導入すると階層ベイズモデルになる。母数を固定した確率分布を与えてやれば階層化されていないので、ベイズ化されたGLMM である。
　(a)は、ランダム切片モデル、(b)は、ランダム係数モデルに該当する。

(2)　格付け推定の階層ベイズモデル
　しきい値メカニズムで格付け推定する階層ベイズ化したGLMMの場合、ランダム切片モデルよりもランダム係数モデルを選択すること多いと感じる。これは、理に適っていると思われる。なぜなら、業種の違いや地域差を説明変数を通じて、推定モデルに反映させたいという明確な目的があるからである。
　階層ベイズ化したGLMM(ランダム係数モデル)の場合、次のように事前確率分布を選択することが多い。説明変数の線形和である線形予測子＝潜在変数、における係数(パラメータ)は、母数がμ、σである正規分布に従う。階層モデルなので、μ、σは確率分布に従う。μは、母数(超事前分布の母数なので、ハイパーパラメータと呼ばれる)がμ₀、σ₀の正規分布に従うとする。つまり、超事前分布が正規分布であるとする。なぜなら、正規分布の平均に対する自然共役な事前分布は、正規分布だからである。ここで超事前分布の母数μ₀、σ₀は定数とする。
　もちろん、さらに確率変数とすることは理屈上は可能であるが、深すぎる階層モデルには、それほど意味はない。超事前分布は、階層ベイズモデルで新たに導入された多数のパラメータをコントロールするために導入されるからである。従って、いわゆる初期値として設定しなければならない。自然共役な事前確率分布については、Ⅳ(3)を参照。
　正規分布の分散に対する自然共役な事前分布は、逆ガンマ分布であるため、σは逆ガンマ分布に従うと設定することが多い[※これは、もちろん金融に限定されることではない]。
　多変量の場合、分散σは分散共分散行列となる。多変量正規分布の分散共分散行列に対する自然共役な事前分布は、逆ウィシャ－ト分布であり、そう設定されることが多い。逆ウィシャ－ト分布は、逆ガンマ分布の多変量バージョンである(なおウィシャ－ト分布はカイ2乗分布の多次元バージョンである)。逆ウィシャ－ト分布のハイパーパラメータ(母数)も定数とする。深すぎる階層モデルにはしない。逆ウィシャ－ト分布の母数は、尺度行列と自由度パラメータである。自由度パラメータは、ベイズ推定の対象となる、線形予測子に現れる係数の数に等しい。一般には切片を考えれるので、説明変数の数＋1となる。

(3)　LGDの推定・概論
　前項ではLGDの推定が、本来難しいことに加えて、日本固有の事情があり、数学的にも困難が伴うと書いた。本項では、LGDのモデル化にあたって留意すべきことを述べる。
　LGDの統計モデルを構築しパラメータを推定すること(以下、LGD推定)は、PDの推定に比べて、一般に難しい。LGD推定の基礎となるデータは、デフォルト債権からの回収額である。回収期間は一般に5～7年程度で長く、そもそもデータが少ない。100％回収は難しいので、ある時点で回収完了とするが、その判断も必要となる。また、回収は保全回収と信用回収とに分かれるが、例えば保全回収は債権者の回収行動に大きく影響されるとされており、両者は分離して推定すべきとされている。
　さらには日本固有の事情もある。デフォルト後の追加融資や経営支援は、日本に限定されないが、日本の場合デフォルト前後で、金利が変わらないといった慣習がある。その代わりに根抵当(などの複雑な担保契約)や連帯保証人制度あるいは信用保証協会保証制度があり、それらが回収金額をカバーしている。
　数学的(統計学的)には、LGDは0%と100%に集中する二峰型分布であるため、パラメータ推定が安定でないとされているので、LGD推定は難しい。
　WinBUGSには｢打ち切りデータ｣に対応する特殊な構文が用意されているので、LGD推定にWinBUGSは向いていると言える。製薬業界ではWinBUGSが多用されている理由の一つは、この特殊構文にあると思われる。

(4)　LGDの階層ベイズモデル化
　LGD推定を階層ベイズモデルで行う場合には、以下の2つのアプローチが(主に実証分析で)用いられている。①LGDがベータ分布に従い、ロジットリンク関数でパラメータを推定するGLMあるいはGLMM。②LGDではなく、回収額(信用回収にかかる回収額)がガンマ分布に従い、対数リンク関数でパラメータを推定するGLMあるいはGLMM。
　GLMもGLMMも、目的変数の期待値を説明変数の線形和でつなげるというアイデアがポイントである。このため、期待値がどう表現されるか？が重要となる。①目的変数がベータ分布に従うとしているから、ベータ分布の期待値がどう表現されるかを示そう。ベータ分は、2つの母数(αとβ)を持ち、期待値はα/(α＋β)で表される。期待値(＝線形予測子)をμとすると、統計モデル上は、目的変数～B(α、(1－μ)/ μ×α)と表現することになる。②ガンマ分布も母数は2つある。形状母数ｋと尺度母数θである。期待値μは、ｋθであるから、統計モデル上は、目的変数～Γ(ｋ、μ/ｋ)となる。
　統計モデル業界では緑本と呼ばれる有名な｢久保拓弥、データ解析のための統計モデリング入門、岩波書店、2012年｣には、割算値を統計モデルの目的変数として使用することを戒めている(pp.130-134)。同書では(情報が失われること以外に)その理由を『分子･分母にそれぞれ誤差を含む数値同士を割った値が従う確率分布の導出は、一般に難しい。分子と分母が独立でない場合は、なおさらである。』と記述している。LGDの場合、分子はEAD－回収額、分母がEADになる。回収額は一般にEADと独立でない(EAD･大⇒信用回収額･小)と認識されているから、LGDが従う確率分布の導出は原理上難しい。
　LGDにおいて測定される数値はあくまで回収額であり、LGDという数値ではない。LGDは単に(リスク管理の)便宜上、導入されたに過ぎない。だとすると理屈上、LGDは目的変数とすべきではなく、回収額を目的変数とすべきとなる。従って、②のように回収額を目的変数とするモデルが望ましいということになる。
　割算値を回避するにはオフセット項を導入すれば良い(ことが緑本に記されている)。平たく言うとオフセット項は、割算値における分母であり、LGDで言えばEADである。なお、オフセット項は、係数(パラメータ)がつかないという性質を持つ。

【4】住宅ローンにおけるMCMC
(1)　順序プロビット、順序ロジットモデル
①事業性融資と同様に信用力でグルーピングして、デフォルト率を推定する手法。
　事業性融資における格付け推移やデフォルト率推定で用いられる、順序プロビットあるいは順序ロジットと呼ばれる統計モデルは、瞬間的な数値を推定対象としている。このため短期(1年以内)では相応の精度を期待できるが、中長期では、精度が低いとされている。事業性融資は短期貸付が多く、長期貸付の場合であっても1年毎に審査する(格付けを見直す)のであれば、順序プロビットあるいは順序ロジットの適用は妥当であると考えられる。
　住宅ローンの場合は、ヴィンテージやシーズニングの議論がある。ヴィンテージは貸付した年に関係する固有の理由から、貸付年毎にデフォルト率が異なるという性質である。シーズニングは、いわゆる期間構造(タームストラクチャ)であり、ある年限(10年程度とみなされることが多い)まではデフォルト率が上昇し、それ以降は、デフォルト率が低下するという現象である。
　斯様な性質を持つ住宅ローンは、順序プロビットあるいは順序ロジットの適用が妥当かという議論が当然存在する。ただし日本の住宅ローンは、十分な担保を確保し、もともとデフォルト率が低い。このため、住宅ローンでは債務者区分(正常先、要注意先･･･)で管理することで、事業性融資と同様の枠組みが適用できると考えられる余地は十分にある。
　なお、住宅ローンのデフォルト率の推定において、地域の違いまで考慮することは、一般的には行われていないと思われる。地域の違いまで考慮した場合には、事業性融資の場合と同様に、モデルが複雑になり、最尤法によるパラメータ推定が困難となる。このため、MCMCの出番となるが、デフォルト率の低さを鑑みると、地域の違いまで考慮してデフォルト率を精緻化するインセンティブは小さいと思われる。それでも仮に、住宅ローンにおけるデフォルト率を、地域の違いを考慮するとしたら、事業性融資の場合と同様に、ランダム切片モデル、ランダム係数モデルを採用することになるだろう。

②信用力でグルーピングせずにデフォルト率を推定する手法。
　信用力スコアを基に、正常先、要注意先等の債務者区分に分別した後に、デフォルト率を推定するのではなく、直接デフォルト率を推定する手法もある。当該手法では、信用力スコアからデフォルトするかしないかを、判別する。デフォルト率は信用力スコアと結び付ける。
　当該手法でも、統計モデルは二項プロビット(二項ロジット)モデルである。しきい値メカニズムが、0(デフォルトしない)と1(デフォルトする)となり、それに応じてリンク関数を調整する必要がある。

(2)　ハザードモデル
　先に、事業性融資と同様の枠組みが適用可能と書いたが、事業性融資では、数値モデル(統計モデル)を使って格付け推定を行い、貸付先の信用リスクを管理している。対して、住宅ローンで行われている、延滞日数による債務者区分管理は｢経験的アプローチ」に該当し、より高度化すべきという議論もある。さらに、フォワードルッキングなアプローチにはなじまないため、期間構造を反映させたデフォルト率の推定を行うという方向に移行することは避けられない。
　その場合、統計モデル的にはハザードモデル－中でも、コックスの比例ハザードモデルが採用されることになるだろう。同モデルでは、ハザード関数を、(生存)時間のみの関数と、exp(説明変数の線形和)との積で表現する。生存時間のみの関数をベースラインハザード関数と呼ぶ。そして、ベースラインハザード関数のみを推定する。
　具体的には、生存時間がワイブル分布Weib(α、β)に従うとすることが一般的である。ここで、αは形状母数でβは尺度母数である。αを一定にしてβを大きくすると正規分布に近づく。一方、βを一定にしてαを小さくすると分布の尖度が大きくなる。MCMCの文脈では、以下のような建て付けになる。
　ワイブル分布の尺度母数を線形予測子とし、対数リンク関数を使う。線形予測子の係数(パラメータ)に事前分布を設定する。形状母数にも適当な事前分布を設定する(もしくは固定値とする)。

(3)　住宅ローンにおけるLGD推定
　事業性融資では、担保で貸し倒れリスクを管理(ヘッジ)するのではなく、事業の将来性評価をベースにリスク管理する方向に移行せざるをえない。その場合は、信用回収額の評価が重要になるので、統計モデルを構築し、数理的にリスク管理するというインセンティブが働く。もっとも、データの蓄積がないため、2025年頃まで待たなければ実用的なモデル構築は難しいかもしれない。
　翻って、住宅ローンでは、無担保融資という流れが一般的にはならないだろうから、将来の信用回収額を予測する統計モデルの構築に対するインセンティブは小さいだろう。

↑目次に戻る

　驚くべき性質★『適切な条件を課したMCMCでは、任意の初期値から初めても、(要する時間は別として)適当なタイミングで定常分布に収束する。定常分布は、所望の事後分布である。つまり、定常分布に収束した後のMCMCで生成される乱数は、事後分布からの乱数となる。』
　驚くべき性質★を保証するアルゴリズムは、たくさん存在する。原型は、メトロポリス･ヘイスティング(MH)法、ギブスサンプラー(別名、熱浴法)である。統計学の分野では、ギブスサンプラーが使われることが多い。
　物理学等の分野では、さらに発展させた(高速化した)タイプであるHMC(ハミルトニアンモンテカルロ法)や、NUTS(No-U-Turnサンプラー)も使われる。ただし、統計分析プラットフォームであるStanにHMC(正確には、NUTS)が実装されているので、使用される場面も増えていると推量される。

　(1)　MH法　
　MH法とメトロポリス法を混同した記述もあるが、両者は異なる(それについては、このセクションの末尾を参照)。MH法の具体的ステップは以下の通り。
　　　①適当な確率分布(提案分布)からサンプリングする。
　　　②詳細つりあい条件を満たすように、確率分布を補正する。
　サンプリングとは、統計モデルの確率分布を使って乱数を発生させることを意味する。

　驚くべき性質★は、どのような形の提案分布を選択しても保証される。それ自体、驚くべきことである。また、具体的に②を書き下すと、②-1：採択のしきい値に該当する｢受理確率｣[注3] と呼ばれる値(αとする)を計算し、②-2：[0,1]の一様乱数と比較して、受理確率αが大きかったら、生成した乱数を今回のステップで採用する。つまり値を更新する。②-3：一様乱数と比較して、受理確率αが小さかったら、生成した乱数を捨てる。つまり前回のステップの乱数をそのまま採用し、値を更新しない。
　受理確率が一様乱数と比べて大きかったら採用するとは、本質的に、「前ステップより尤度が大きくなったら、今回生成した乱数を採用する。」ということを意味している。
　メトロポリス法、独立MH法、ランダムウォークMH法というのは、もちろんMH法の仲間で、提案分布Qの性質によって分別されている。
　例えば、メトロポリス法は、提案分布Qが対称性を有する。すなわちQ(x,y)＝Q(y,x)である。正規分布は対称性を持つから提案分布として正規分布を選べば、メトロポリス法ということになる。対称性を課すという強い制約のおかげで、メトロポリス法の受理確率はシンプルな形となる。その反面、メトロポリス法は推移前の状態が強く影響するために、(他のMH法よりも)状態推移に時間がかかると考えられる。
　密度関数をｆとしたとき、提案分布Q(x,y)が、Q(x,y)＝ｆ(y)で表されるとき、独立MH法という。Q(x,y)＝ｆ(y－x)で表されるときは、ランダムウォークMH法という。
　いずれにしてもMH法は、提案分布の選択が収束時間に大きく影響するアルゴリズムである。

　(2)ギブスサンプラー　
　提案分布が違うだけという意味では、ギブスサンプラーもMH法の一種であるが、遠い親戚といった方が適切かも知れない。提案分布Q(x,y)が条件付き事後分布Pr(y|x)に等しいとき、MH法はギブスサンプラーと呼ぶアルゴリズムに等しい。
　ギブスサンプラーの考え方自体は古くいろいろな分野で独立に発見されている。統計物理学の分野では熱浴法として1979年に知られていた。
　Geman and Gemanは画像復元のアルゴリズムとして、独立に発見した(1984年)。Geman and Gemanはギブス分布への応用としたためギブスサンプラーと名付けた。
　条件付き事後分布Pr(y|x)を書き下すことができれば(＝条件付き事後分布関数の形が予め分かっていれば)、ギブスサンプラーは使用可能であるし、効率的なサンプリング法である。なお｢条件付き｣とは、多変量確率分布から1つの変数(変量)を脇に置いて、他の変数を全て定数とすることを指している。
　具体的なステップは以下の通り。
　　　①初期値を適当に決める。
　　　②条件付き確率から新しい値を逐次的に発生させる。

　これだと全くピンとこないので少し数式で書く。
　　　①初期値b₁、b₂を適当に決める。
　　　②条件付き事後分布Pr(b₁|b₂)に従う乱数を発生させて、それを新しいb₁とする。
　　　③Pr(b₂|新しいb₁) に従う乱数を発生させて、それを新しいb₂とする。
　　　④このステップを繰り返す。

　MH法は棄却がもったいない＝値が更新されないことも多い。という批判がある。ギブスサンプラーは棄却しない。常に受理･更新する。その意味では速い。
　しかし、常に受理･更新するからこそ、条件付き事後分布から乱数を生成できないと、アルゴリズムとして成立しない。そのような場合は現実的にはレアということで、その問題を解消する手段として、格子点ギブスサンプラーやMH法と組み合わせるMetropolis within Gibbsが存在する。ただし前者は、ほとんど使われていないようである。

　(3)　ハミルトニアン･モンテカルロ(HMC)法　
　提案分布が異なるだけ、という意味でHMC法もMH法の一種である。HMC法は、統計物理で使われている分子動力学法(MD)に起源を持つ。
　物理屋さんはハイブリッド･モンテカルロ(同じくHMC)法と呼ぶ。MDとMH法のハイブリッドという意味合いのようである。1987年にSimon Duane他によって、量子色力学用の効率的な数値計算アルゴリズムとしてフィジクスレターBに発表された(原論文はこちら)。 数学的には経路積分－もちろん多重の経路積分－を計算するためのアルゴリズムである。
　MCMC法はパラメータ空間を、乱数発生アルゴリズムに従ってランダムに探索するが、前ステップの影響を受けるがために、網羅的な探索が難しい。比喩的に言うと、破天荒な行動はとらないので、探していないパラメータ空間に到達するまでの時間がジレッたい。
　物理的(解析力学的)バックグラウンドを利用して、遠くまで探索するようにMH法を改良した手法がHMCである。また比喩的に言うと、ハミルトニアン保存という足枷を付けた上で、破天荒な探索行動をたまに行うことを許容している、と言えるだろう。
　HMC法では、乱数生成にハミルトニアンを利用するために、仮想的な運動量を補助変数として導入している。位置x、運動量pで張られる空間において、時間発展を表現する写像fをマルコフ連鎖の遷移と考える。(x,p)空間の確率密度関数qがハミルトニアンだけの関数であれば、ｑはマルコフ連鎖の定常分布となる。こうして物理(ハミルトニアン)とMCMCが結びつく。[参考1]
　時刻Tにおける(x,p)を代入したハミルトニアンから、初期状態の(x,p)を代入したハミルトニアンを引いた値をΔHとすると、受理確率α＝min[1,exp(-ΔH)]である。時刻Tにおける(x,p)はハミルトン方程式(当然、微分方程式)を解くことで得られる。

　(4)　NUTS　
　HMC を実行する際には、ステップ幅εと終端時刻Tのファイン･チューニングが必要である。具体的には、ハミルトン方程式を解いて生成するパスの長さを、いい感じに決める必要があり、その方法を実装したHMCがNUTSである。より具体的には、パスにUターンが生じたとき、詳細つり合い条件を破らないように「そこでパスを止める」工夫を施している。パスを止める目安があるために、無駄打ちが減って効率的という理屈である。

　(5)さらに進んだ話題　
　最後に、さらに進んだ話題として、高速化を目指したアルゴリズムの話題①～④と、尤度の計算が困難な場合にパラメータを推定する方法⑤を取り上げる。

　①詳細つり合い条件を満たさないMCMC
　驚くべき性質★『適切な条件を課したMCMCでは、任意の初期値から初めても、(要する時間は別として)適当なタイミングで定常分布に収束する。定常分布は、所望の事後分布である。つまり、定常分布に収束した後のMCMCで生成される乱数は、事後分布からの乱数となる。』で触れた、「適切な条件」とはエルゴード性とつり合い条件である。しかし、一般的には、エルゴード性と詳細つり合い条件を課す。詳細つり合い条件を課すと受理確率αの決定が簡単になるからである。その代償として、収束時間は遅くなる。
　近年では高速化を目指して、つり合い条件を満たすが詳細つり合い条件を満たさないSuwa-Todo法やSakai-Hukushima法と言ったアルゴリズムが導入されている(らしい)。

　②ランジュバン･モンテカルロ(LMC)法
　LMC法で乱数を更新する式(更新式)は、ランジュバン方程式と結びついている。具体的には、HMCのステップ幅εを0とする極限で、更新式がランジュバン方程式となる。
　ハミルトニアンの勾配方向に移動してノイズを加える、というプロセスで新しい乱数を生成する。棄却を前提としていないが、棄却されない(値が更新しない)ことを保証するわけではない。

　③リーマン多様体モンテカルロ(RM-HMC)法[参考1]
　HMC法は、トロい探索を破天荒な探索で置き換えて、高速化を目指した。HMC法では射程外であった｢変数間の"線形"相関が高い｣場合に、高速化を目指したアルゴリズムが、リーマニアンモンテカルロ法である。ただし万能でも汎用的でもないようであるから、採用されるケースは限定的と思われる。
　RM-HMC法では、ハミルトニアンにおいて運動量をどのように組み入れるかを工夫することで、高速化を図っている。

　④レプリカ交換モンテカルロ法
　複数の系(レプリカ)を一定の規則で交換することで乱数生成を効率化するアルゴリズム。具体的には、以下の通り：
　　a.パラメータを少しづつズラして複数の系(レプリカ)を作る。
　　b.レプリカを同時にシミュレーションする。
　　c.受理確率αに従って、隣同士のレプリカを定期的に交換する。
　MH法と同様に[0,1]の一様乱数と比較し、受理確率が大きかったら交換する。小さかったら交換しない。

　⑤近似ベイジアン計算(ABC)
　これまでの話題とは全く毛色がことなる話題である。尤度の計算が困難な場合に(ベイス推定の範囲で[注4])どうパラメータを推定するかという話題である。ただし、尤度の計算は困難であるが、尤度関数からのサンプリングは可能とする。近似ベイジアン計算(ABC)というアプローチが答えの一つである。ABCは集団遺伝学の分野で提案されたのが始まりである。金融分野では、損害保険の保険給付支払金準備金の分析、オペレーショナルリスク分析などで利用されている。
　棄却サンプリングと呼ぶ手法では、以下の様に乱数を生成する。
　　　a. 事前確率分布から乱数(パラメータ)を生成する。
　　　b. 乱数(パラメータ)を使って尤度関数から乱数(推定観測データ)を生成する。
　　　c. 実測観測データと、推定観測データとの距離を計算する。
　　　d. 距離が、設定したしきい値より小さい場合に、乱数(パラメータ)を受け入れる。
　　　e. 収束条件を満たすまで、作業を繰り返す。

　距離は、ユークリッド距離でも良い。効率的に乱数を生成させたい場合には、カスタマイズすることもある。
　しきい値εを0に近づける極限で、ABCで得られる乱数は、事後確率に従うことが数学的に示されている。

　棄却サンプリングより効率が良い、MH法に類似したMCMC-ABCという手法が存在する。
　　　1. 提案分布から乱数(パラメータ)を生成する。
　　　2. 乱数(パラメータ)を使って尤度関数から乱数(推定観測データ)を生成する。
　　　3. パラメータと推定観測データを受理確率[注5]に従って採用する。

　MCMC-ABCとは違うアプローチで乱数生成を効率化する手法として、要約統計量を導入するという手法がある。棄却サンプリングでは、生のデータ間に対して距離計算を行ったが、データの要約統計量に対して距離計算を行うと効率が上がる。
　他にも効率向上の取り組みとして、回帰調整、パラレルテンパリングの適用、一般化マルチポイントメトロポリス法(GMPM)の適用、逐次モンテカルロ法(SMC)の適用、といった話題がある。

↑目次に戻る

　表題の各テーマについて概観する。

　(1)　モデル選択基準の指標　
　複数のモデルがあったとき、どのモデルを選択すべきかを判断する目安(情報量基準、IC)が数多く存在する。統計ソフトウェアを使用することを前提とすれば、情報量基準はソフトウェアが計算してくれる。そのため、情報量基準の解釈について記述する。
　ここでは主に「AIC、BIC」を扱う。付随的に「WAIC、WBICとDIC」も扱う。
①一致性と有効性
　情報量基準における一致性とは、標本数(データの採取数)が大きくなる時に説明変数の正しい数を選ぶ、という性質をいう。これではわからないので、もう少しかみ砕いて説明する。
　真のモデルTと偽のモデルFがあるとする。もちろんTとFは説明変数の数が異なる。Tからｎ個のデータを採取し最尤推定値を計算する。Fでもおなじようにｎ個のデータを採取し最尤推定値を計算する。ｎを大きくしていっても、Tの(最尤推定値を使った)情報量基準とFの(最尤推定値を使った)情報量基準を区別することができないとする。そのとき、その情報量基準には一致性がない、という。
　一致性がなければ、その情報量基準では、正しい説明変数の数がTの説明変数の数なのかFの説明変数の数なのかを判別できない。つまり真のモデルTと偽のモデルFを区別することが(理論上)できない。
　一致性と対で議論される、情報量基準の性質に有効性がある。次の場合a及びbに、情報量基準が、cを満たすとき、その情報量基準は、有効性がある、という。
　　a.　真のモデルが真のモデル候補に含まれていない場合。
　　b.　標本数を∞に近づけた場合。
　　c.　真実のモデルとの予測誤差が最小になるモデルを選択可能。

②AIC(赤池情報量基準)
　AIC以前には、モデルを評価･選択するという発想自体がなかったらしい。AICは、「手元にあるデータへの当てはまりが良いモデルではなく、新しく得られるデータを高精度に予測できるモデルが、良いモデル」という発想で開発されている。
　AICは、平均予測誤差の近似値であり、最尤推定量が求まってれば計算できる。難しく言うと、以下の通り。
　　　a.　カルバック-ライブラー(K-L)情報量を計算する。
　　　b.　最尤推定値はK-L情報量を最小化する値である。
　　　c.　最大対数尤度は、最尤推定値で計算したK-L情報量の近似値である。
　　　d.　AIC＝－2×最大対数尤度＋2×説明変数の数
　K-L情報量は、真のモデルと推定モデルの距離に類似する量である。このAICで完璧に思えるが、なぜ他の情報量基準が要求されるのか･･･。それはAICは、一致性がないからである。
　AICは、｢真のモデル候補｣の中で、その値が最も小さいモデルを選ぶという使い方をする。AICは相対的な指標であるから、特定の値より小さければそのモデルを選択する、という使い方は出来ないことに注意。AICは、真のモデルを選択できるわけではなく、｢真のモデル候補｣の中でどのモデルが相対的に予測誤差が小さいかを選択できる、に過ぎない。
　なお、フィッシャー情報行列が正則でなくても使用できる、また説明変数が階層構造を持つために最尤推定できない(推定結果が不安定になる)場合にも使用できる、ように拡張したAICとしてWAIC(Widely applicable AIC)がある。

③BIC(ベイズ情報量基準)
　BICは、複数用意したモデルの中で、(ベイズ理論における)事後確率が最も高いモデルを選択する情報量基準である。最高の事後確率をもたらすモデルが最も良いモデルという(ベイズ的な)発想である。BICの見た目は、AICとすごく似ている。
　　　　　　BIC＝－2×最大対数尤度＋log(標本数)×説明変数の数
　AICとは異なり、BICは一致性を持つことが知られている。標本数ｎを無限大に近づけるに従って、真のモデルを選択する確率が100％に近づく。
　それではBICを選択基準にすれば、この話は終わりか？というと、そうでもない。そもそも一致性は、真のモデルが、｢真のモデル候補｣に含まれている、という仮定があって始めて議論できる。しかし複雑な対象をモデル化する実務において、それは現実的ではない。そうすると一致性の議論自体、重要ではないとなる。
　AICには一致性はないが、有効性がある場合がある。当然BICに有効性はない。
　BICも、｢真のモデル候補｣の中で、その値が最も小さいモデルを選ぶという使い方をする。BICも相対的な指標であるから、特定の値より小さければそのモデルを選択する、という使い方は出来ないことに注意。
　なお、フィッシャー情報行列の正則性が成立しなくても使用できる、また説明変数が階層構造を持つために最尤推定できない(推定結果が不安定になる)場合にも使用できる、ように拡張したBICとしてWBIC(Widely applicable BIC)がある。

④AICとBIC。結局、それでどうするの？
　結局、どうするの？ということだが、AICとBICが同じモデルを選択するということは珍しくない。もちろん違うモデルを選択するケースもある。一致したら文句なく、そのモデルを選べば良い。
　違っていたら、どうするか。もし、AIC最小モデルの説明変数･数が、BIC最小モデルの説明変数･数より小さいというのは変だろう。なぜなら、AICは説明変数が多いモデルを選ぶ傾向があるからである。その場合は、BIC最小モデルを選べば良いのではないだろうか。
　残りは、AIC最小モデルの説明変数･数が、BIC最小モデルの説明変数･数より大きい場合であるが、AICとBICのどちらを選ぶか決め手がないのであれば、他ケースと平仄を合わせるという消極的な理由でBICを選んでも良いように思える。

⑤DIC(偏差情報量基準)
　説明変数が階層構造を持つ場合、説明変数の数をどうカウントするかには不定性があるため、AICやBICは適用できないという思想の下、考案された情報量基準がDICである。
　説明変数が階層構造を持つ場合のパラメータ推定法としては、最尤法は適格ではなく、MCMCが妥当な手法であると考えられている。
　DICはMCMC用の情報量基準と言えるが、DICの適用には各種議論があるようで、あまり使われていないようである。

⑥結局、MCMC用の情報量基準は何を使うのか。
　AICやBICを説明変数が階層構造を持つ場合に拡張した、WAICもしくはWBICを使うことが妥当のようである。

　(2)　収束性判断の指標　
　モデル選択の指標(情報量基準)と同様に、収束性判断の指標も完全な指標は存在しない。統計ソフトウェアを使用することを前提とすれば、収束性判断の指標はソフトウェアが計算してくれる。そのため、解釈について記述する。

①Gelman-Rubinの収束診断
　定常分布が正規分布と大きく異なる場合は収束判断に誤りが発生すると考えられるが、以下のようなステップで、ポテンシャルスケ－ル減少係数(PSRF)という数値を計算し、収束性を判断する。
　　a.　定常分布が正規分布であるマルコフ連鎖を考える。
　　b.　発生された標本の分布をt分布によって近似する。
　　c.　t分布で近似した標本分布の分散と定常分布の分散からPSRFを計算する。
　　d.　PSRF値が1に近ければ[注6]収束したと判断する。
　なお、PSRFをR^と表記することは一般に行われていて、PSRF自体、そう呼ばれることは少なくアールハットという呼称が広く使われる。つまり、MCMCの文脈でアールハットという言葉が現れたら、PSRFが1に近いかを見ることで収束を判断している、と考えて良い。

②Raftery and Lewisの収束診断
　バーンイン回数[注7]を理論的に導くアルゴリズムである。長いマルコフ連鎖からｋ個おきに標本を抽出するという仮定を置いている。このｋは、指定した推定精度を満たすように観測値から推定する必要がある。合わせて推移行列の要素も推定する必要がある。
　理論的に導かれたバーンイン回数MとMCMC回数Nから、DependenceファクターIを計算する。Iが大きい(一般的には5超)の場合、収束していないと判断する。 標本百分位数の収束を用いる場合以外は、収束判断を誤ることがあると言われている。

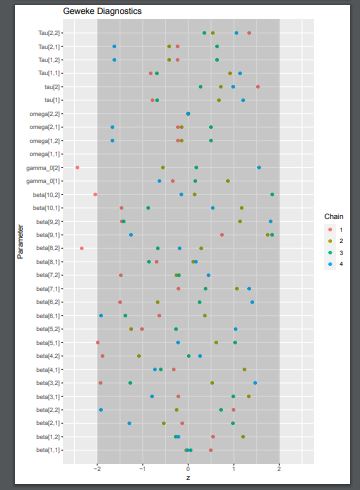
③Gewekeの収束診断
　有意水準5％での検定を用いて収束判断を行う。
　得られた標本系列の前半(通常は、10%)と後半(通常は、50%)で、マルコフ連鎖を成すパラメータθの関数g(θ)の期待値が同じかどうかを仮説検定する。
　具体的には、θの関数g(θ)と、gのスペクトル密度Sを用いて計算したZ統計量(の絶対値)が
　　　　　　　　　｜Z｜≦ｚ_α/2
のとき収束していると判断する。ｚ_α/2は標準正規分布の上側2.5％点(z値1.96)である。従って｜Z｜が1.96以下だと収束していると判断される。
　適当なスペクトルウィンドウ(あるいは窓関数)を採用していない場合は、収束性判断に誤りが生じると言われている。

①無情報事前確率分布
　ベイズ統計モデルでは、パラメータ推定において、事前確率分布を設定する必要がある。最もシンプルな例は、[－∞,∞]の範囲で好きな値を採るという確率分布である。これを無情報(一様)事前分布と呼ぶ。始祖ベイズが考えた由緒ある設定であるとともに、ベイズ統計学を最初に体系化したラプラスも使用していたため、ベイズ･ラプラス事前分布とも呼ばれる。もちろん現実的には、∞はコンピュータ上で表現できないので、大きなべき乗で代用する。
　[－∞,∞]の一様分布以外では、平均ゼロで分散が非常に大きい｢平らな｣正規分布が用いられる。

②自然共役事前確率分布
　尤度関数に対して、事後確率分布が事前確率分布と同じ分布族(ファミリー)となる事前分布を、(自然)共役事前分布という。つまり、この場合は、事後確率分布自体を推定する必要はない。事後確率分布のパラメータだけを推定(計算)すれば良い。
　MCMC以前は、このような便利な性質を利用しなければ、ベイズ統計モデルを活用することができなかった。その意味で、歴史的な遺産と言えよう。
　条件付共役自然分布＝母数が複数ある時、特定の母数を既知とした場合の尤度関数に対して共役となる事前分布を条件付自然共役事前分布と呼ぶ。単変量正規分布において平均が既知とした場合の分散に対する条件付自然共役事前分布が、逆ガンマ分布である。

③階層事前確率分布
　事前確率分布Pのパラメータに、さらに事前確率分布Qが設定されている場合、Pを階層事前確率分布と呼ぶ。『Ⅰ概要　【2】統計モデルとパラメータ推定法－MCMCはパラメータ推定法である！　(3)MCMCと一般化線形混合モデル(GLMM)』の[C]で説明した、確率分布を合成するという話と符号するだろう。
　Pの(事前確率分布Qが設定されている)パラメータを超パラメータと呼ぶ。Qは超事前確率分布と呼ばれる。
　階層事前確率分布を使っているベイズ統計モデルを、階層ベイズモデルと呼ぶ。

↑目次に戻る

　パラメータ推定法という枠組みでMCMCを捉えて理解しようとすると、必然的に、最小二乗法や最尤法というパラメータ推定法と対応する統計モデルの理解が必要になる。なぜなら最小二乗法や最尤法が、どういう状況になれば適用できなくなって、MCMCにその座を奪われるかを理解する必要があるためである。
　そのような意識で成書を探すと、意外と良書は少ないと感じる。そんな中で、とても印象に残ったのが｢久保拓弥、データ解析のための統計モデリング入門、岩波書店、2012年｣である。同書は、業界(？)では緑本と呼ばれる有名な書籍のようである。
　ただ同書の想定読者は、あくまで研究者であるから、実務家からは、説明がやや天下り的と思える箇所が散見される。そう言った箇所を補ってくれる成書があれば、実務家としては助かるだろうと思う。

(1)サイト移転情報
　緑本には、同書で扱われているデータセットやコードの格納サイトが記されているが、2020年時点では移転している。移転先は、以下の通り。
　https://kuboweb.github.io/-kubo/ce/IwanamiBook.html

(2)RとWinBUGSとStanに関する情報
①Rの最尤推定関数
　glmmML関数は、二項分布とポアソン分布しか扱えない。正規分布やガンマ分布はglmer関数を使う。

②WinBUGSの事前確率分布
　WinBUGSのサンプリングは、事前確率分布が自然共役事前分布である場合は、ギブスサンプラーを使用する。事前分布が自然共役事前分布でない場合は、以下の様にサンプリングする[参考2]。
　まず、目標とする事後分布が連続分布の場合は、以下の通り。
　a) 条件付事後分布が対数凹関数の場合は Derivative-Free Adaptive Rejection Sampling
　b) サンプリングされる値の範囲が制限されている場合はスライスサンプリング。
　c) サンプリングされる値の範囲が制限されていない場合は Current point メトロポリス法(注8)
　次に、目標とする事後分布が不連続分布の場合は、以下の通り。
　d) 上限が有限の場合は Inversion 法。
　e) Shifted Poisson は，標準的な乱数発生アルゴリズムより発生させる。

③Stanの長所
　a. 自己相関性低減により収束性が向上する。
　b. 事前確率分布として半コ－シ－分布を使える。半コ－シ－分布は、発生事象が少ないイベントを扱う場合でもフィットする。
　c. Stanではthinning = 10で十分に自己相関を減らすことができるが、BUGSではthinning=100でも十分に自己相関を減らすことができない。つまり、Stanは少ないサンプルで済む。

(3)Rの追加パッケージ
　例えば、glmmML関数をインストールするには、R(RStudio)で以下の様にコマンドを打つ。
　　> update.packages()
　　> install.packages("glmmML")
glmer関数なら
　　> install.packages("lme4")
とする。

(4)bugs関数の結果である、推定したパラメータのトレ－スプロットと事後分布を、描画してpdfファイルに出力する方法。
　パラメータの従う確率分布が多変量(正規分布)である場合で、説明変数が多数ある場合、推定結果は数十になることもある。それを、(RStudioの)画面上で確認することはできないので、ファイルに出力する必要がある。その方法は意外な程、どこにも示されていないので以下にまとめた。

　①bugs関数の引数に、codaPkg=TRUE　を付け加える。★重要！
　> result.MCMC <- bugs(data, inits,parameters, "file_name.txt", n.chains=3,n.iter=1000, working.directory=getwd(), codaPkg=TRUE)

　②read.bugsで、MCMCの結果を変換する。なおcoda フォーマットに変換しておくと、下記例で言うと、gelman.diag(result.coda)あるいはgeweke.diag(result.coda)と入力することで、収束診断結果の出力が可能となる。前者はGelman-Rubinの収束診断(いわゆるRハット)である。後者はGewekeの収束診断である。Raftery and Lewisの収束診断の場合は、raftery.diag(result.coda)とする。
　またautocorr.diag(result.coda)とすれば、自己相関診断ができる。
　> result.coda <- read.bugs(result.MCMC)

　③PDFファイルを開く。
　適当な名前をつける。この例だと、WinBUGSの作業フォルダに、fig.pdfという空のPDFファイルが作成される。なおPDF以外にもJPEG形式などでも可能。
　> pdf("fig.pdf")

　④描画する。
　> plot(result.coda)
　fig.pdfという空のPDFファイルに、トレ－スプロット(MCMC 計算遷移図)と事後分布の密度関数図が一緒に描画される。個別に描画したい場合は、それぞれtraceplot(result.coda)、densplot(result.coda)とすれば良い。

　⑤手放す(リリースする)。
　> dev.off()
　このコマンドを打たないと、ファイルを開けない(Rがファイルをリリースしてくれない)。②～⑤は予めスクリプトファイルに書いておけば良い。

(5)stanによる推定結果を、描画してpdfファイル(ファイル名：●●.pdf)に出力する方法。
　①予めggmcmcライブラリをインストールしておく。
　> install.packages("ggmcmc")

　②stanによる推定を行う前にライブラリを展開する(スクリプトに書いておく)。
　> library(ggmcmc)
(stanによる推定とは、つまり
　> stan_result <- stan(file = "●●.stan",data = data_list,seed = 1,iter=5000,warmup=1000,chains=4)
を実行するということ。●●.stanはモデルを記述したスクリプトファイル。)

　③以下のコマンドを実行する(スクリプトに書いておけばいい)。
　> save.image(file='stan_result.RData')
　> load('stan_result.RData')
　> ggmcmc(ggs(stan_result), file='●●.pdf')

　主な描画対象は以下の通り。ヒストグラム、トレースプロット、デンシティプロット、自己相関、Rハット(Gelman-RubinのPSRF)、Gewekeのｚ値。

↑目次に戻る